Lineare Regression - Methode der kleinsten Quadrate

• ### 1. Einleitung

Während dieser Zeit lernte ich die Logistic Regression in Kapitel 5 und fühlte mich ziemlich anstrengend. Ich ging von der Logistic Regression über die Linearregression und dann über die Minimum-Doppel-Faktor-Faktor-Faktor. Der Minimum-Doppel-Kombination-Rad ist eine Implementierung, die die empirische Formel in der Optimierungsfrage aufbaut. Die Prinzipien sind nützlich für die Lernkette der Logistic-Return-Rad und der Radar-Support-Vektormaschine.

• ### 2. Hintergrundwissen

Der historische Hintergrund für die Entwicklung der Minimalzyklus-Faktorin ist interessant.

Im Jahr 1801 entdeckte der italienische Astronom Giuseppe Piazzi den ersten Asteroiden Ceres. Nach 40 Tagen der Beobachtung verlor Piazzi seine Position, da Ceres hinter der Sonne zurücklief. Später begannen Wissenschaftler auf der ganzen Welt, Ceres mit Piazzis Beobachtungsdaten zu suchen, aber es gab keine Ergebnisse für Ceres nach den Ergebnissen, die die meisten Menschen errechneten.

Die Methode, die von Gauss verwendet wurde, wurde 1809 in seinem Werk Theory of the Movement of Celestial Bodies veröffentlicht, und der französische Wissenschaftler Léger entdeckte 1806 unabhängig die Minimalzyklus der Minimalzyklus, die jedoch unbekannt war, weil sie nicht für die Zeit bekannt war. Zwischen den beiden wurde gestritten, wer die Minimalzyklusprinzipien zuerst erstellt hatte.

1829 erbrachte Gauss einen Beweis dafür, dass die Optimierung der Minimum-Zwei-Multiplizierung besser funktioniert als andere Methoden, siehe Gauss-Markov-Theorem.

• ### 3. Die Nutzung von Wissen

Der Kern der Quadratmeter-Minimum-Doppel-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver-Pulver

Angenommen, wir sammeln Daten über die Länge und Breite von Kriegsschiffen.

Auf der Grundlage dieser Daten haben wir in Python eine Streuungskarte erstellt:

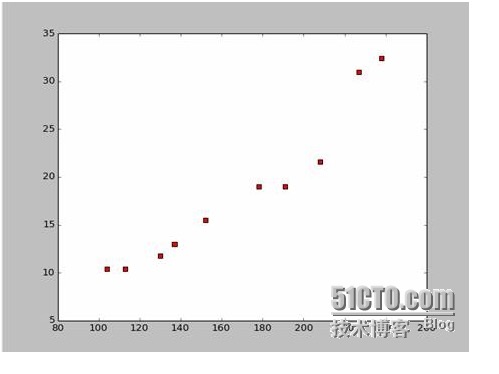
Der Code für die Streichung ist wie folgt:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Wenn wir die ersten beiden Punkte nehmen, 238, 32, 4 und 152, 15, 5 bekommen wir die beiden Gleichungen. 152*a+b=15.5 328*a+b=32.4 Wir können diese beiden Gleichungen lösen und a ist gleich 0,197 und b ist gleich -14,48. In diesem Fall erhalten wir eine Anpassungsgrafik wie diese:

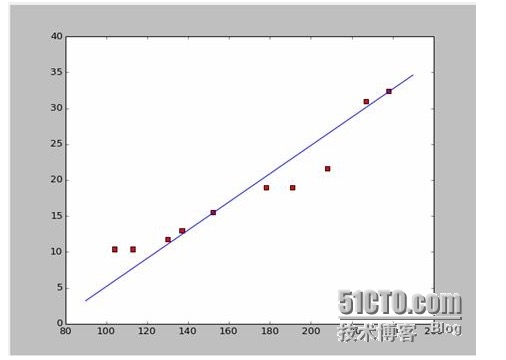
Nun, die neue Frage ist, ob a und b die optimale Lösung sind. Um es professionell auszudrücken, ist a und b die optimale Parameter für das Modell? Bevor wir diese Frage beantworten, müssen wir eine andere Frage beantworten: Welche Bedingungen erfüllen a und b am besten?

Die Antwort lautet: das Quadrat und das Minimum, das die Differenz aller Daten gewährleistet. Das Prinzip wird später erläutert, um zu sehen, wie man mit diesem Werkzeug am besten a und b berechnen kann.

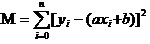
Wir müssen jetzt die beiden kleinsten a und b von M finden.

Die Gleichung ist eine binäre Funktion mit a, b als Eigenvariablen und M als Faktorvariablen.

Denken Sie daran, wie man in hohen Zahlen die Extreme einer Einfachfunktion ausgleicht. Wir benutzen das Werkzeug der Derivate. In einer binären Funktion benutzen wir die Derivate. Wenn wir die Derivate von M anfragen, erhalten wir eine Gruppe von Gleichungen.

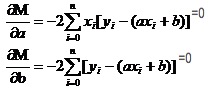
In den beiden Gleichungen sind x und y bekannt.

Es ist sehr einfach, a und b zu finden. Da ich auf Wikipedia zurückgegangen bin, zeichne ich hier ein passendes Bild mit den Antworten:

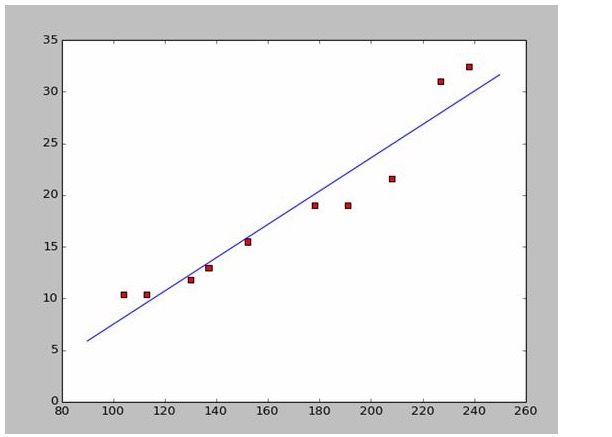
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Vier Grundsätze, die wir erforschen

Warum wird bei der Datenanpassung das Quadrat der Abweichung zwischen den prognostizierten und den tatsächlichen Daten des Modells und nicht die absoluten Werte und die Minima optimiert, um die Modellparameter zu optimieren?

Diese Frage wurde bereits beantwortet, siehe Link (http://blog.sciencenet.cn/blog-430956-621997.html)

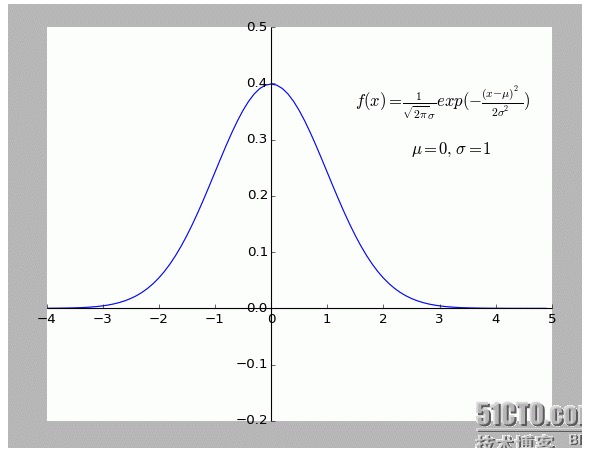
Ich persönlich finde diese Erklärung sehr interessant. Besonders die Hypothese: Alle Punkte, die von f (x) abweichen, sind laut.

Je weiter von einem Punkt entfernt, desto größer ist die Wahrscheinlichkeit, dass dieser Punkt auftritt. Welche Beziehung zwischen der Abweichung x und der Wahrscheinlichkeit f (x) besteht?

• ### 5. Ausdehnung

Die oben beschriebenen Situationen sind zweidimensional, d.h. es gibt nur eine eigenvariable. In der realen Welt sind es jedoch mehrere Faktoren, die das Endergebnis beeinflussen, d.h. es gibt mehrere eigenvariable.

Für die allgemeinen Metall-Linearfunktionen N ist es in Ordnung, die inverse Matrix in der Kettenlinie zu verwenden; da wir keine geeigneten Beispiele vorerst gefunden haben, bleiben wir hier als Argument.

Natürlich ist die Natur viel mehr als eine einfache lineare Anpassung von Polynomen, das ist etwas höheres.

• Verweise

  • Hochschulmathematik (6. Ausgabe)
  • Liniale Algebra (Beijing University Press)
  • Das ist eine sehr schöne Geschichte.Minimaler Zweifacher
  • Wikipedia: Minimaler Zweifachzahl
  • Wissenschaftsnetz:Das Minimum der Zweimalzahl? Das ist kein schlechter Absolutwert für ein Pferd.

Originalarbeiten, Übertragung erlaubt, Übertragung ist in Form von Hyperlinks mit der Originalquelle des Artikels, der Autoreninformation und dieser Erklärung zu versehen. Andernfalls wird die rechtliche Verantwortung übernommen.