Im vorherigen Artikel (https://www.fmz.com/digest-topic/4187) haben wir Paarhandelsstrategien vorgestellt und gezeigt, wie man Daten und mathematische Analysen zum Erstellen und Automatisieren von Handelsstrategien nutzt.

Die Long-Short-Balanced-Equity-Strategie ist eine natürliche Erweiterung der Pair-Trading-Strategie, die auf einen Korb von Handelszielen anwendbar ist. Es eignet sich besonders für Handelsmärkte mit vielen Varianten und Wechselwirkungen, wie etwa den Markt für digitale Währungen und den Rohstoff-Terminmarkt.

Grundprinzipien

Die Long-Short-Balanced-Equity-Strategie besteht darin, bei einem Korb von Handelszielen gleichzeitig Long und Short zu gehen. Bestimmen Sie genau wie beim Paarhandel, welche Anlageziele günstig und welche teuer sind. Der Unterschied besteht darin, dass bei der Long-Short-Balanced-Equity-Strategie alle Anlageziele in einem Aktienauswahlpool bewertet werden, um zu bestimmen, welche Anlageziele relativ günstig sind. Oder teuer. Anschließend wird basierend auf der Rangfolge eine Long-Position bei den n höchsten Anlagen eingenommen und eine Short-Position bei den n niedrigsten Anlagen mit gleichem Betrag (Gesamtwert der Long-Positionen = Gesamtwert der Short-Positionen).

Erinnern Sie sich, als wir vorhin sagten, dass der Paarhandel eine marktneutrale Strategie ist? Dasselbe gilt für eine ausgewogene Long-Short-Aktienstrategie, da die gleichen Beträge an Long- und Short-Positionen sicherstellen, dass die Strategie marktneutral bleibt (nicht von Marktschwankungen beeinflusst wird). Die Strategie ist zudem statistisch robust. Durch die Einstufung von Investitionen und die Übernahme mehrerer Positionen können Sie Ihr Rankingmodell mehreren Risiken aussetzen, anstatt es nur einem einmaligen auszusetzen. Sie wetten lediglich auf die Qualität Ihres Rankingsystems.

Was ist ein Ranking-Schema?

Bei einem Rangsystem handelt es sich um ein Modell, das jedem Anlageziel auf Grundlage der erwarteten Performance eine Priorität zuweist. Die Faktoren können Wertfaktoren, technische Indikatoren, Preismodelle oder eine Kombination aller oben genannten sein. Sie könnten die Momentum-Metrik beispielsweise verwenden, um eine Liste trendfolgender Investitionen zu bewerten: Die Investitionen mit dem höchsten Momentum würden voraussichtlich auch weiterhin eine gute Performance aufweisen und die höchsten Bewertungen erhalten; die Investitionen mit dem geringsten Momentum würden am schlechtesten abschneiden und haben die niedrigsten Renditen.

Der Erfolg dieser Strategie hängt fast vollständig von dem verwendeten Rangfolgeschema ab. Das heißt, dass Ihr Rangfolgeschema in der Lage ist, leistungsstarke Anlagen von leistungsschwachen Anlagen zu trennen und so die Renditen der Long-Short-Anlagezielstrategie besser zu erzielen. Daher ist es sehr wichtig, ein Ranking-System zu entwickeln.

Wie formuliert man einen Rankingplan?

Sobald wir ein Rankingsystem eingeführt haben, möchten wir natürlich davon profitieren. Dies erreichen wir, indem wir den gleichen Geldbetrag investieren, um bei den bestplatzierten Anlagen Long-Positionen einzugehen und bei den schwächsten Anlagen Short-Positionen einzugehen. Dadurch wird sichergestellt, dass die Strategie nur im Verhältnis zur Qualität ihrer Rankings Geld einbringt und „marktneutral“ ist.

Angenommen, Sie ordnen alle Investitionen m, haben n Dollar zum Investieren und möchten insgesamt 2p (wobei m>2p) Positionen halten. Wenn die Investition mit Rang 1 voraussichtlich die schlechteste Performance erzielt, dann wird die Investition mit Rang m voraussichtlich die beste Performance erzielen:

• Die Anlageziele gliedern Sie wie folgt: 1, …, p und Short 2/2p USD Anlageziele

• Sie ordnen die Anlageziele wie folgt an: m-p,……,m, und gehen auf n/2p Dollar der Anlageziele long

Beachten:Da der Zielpreis aufgrund von Preissprüngen nicht immer gleichmäßig durch n/2p geteilt werden kann und einige Ziele in ganzen Zahlen gekauft werden müssen, wird es einige ungenaue Algorithmen geben und der Algorithmus sollte so nahe wie möglich an dieser Zahl liegen. Für die Strategie mit n = 100000 und p = 500 sehen wir:

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

Dies kann bei Preisen mit Bruchteilen über 100 (wie etwa auf Rohstoff-Terminmärkten) zu großen Problemen führen, da Sie keine Positionen mit Bruchpreisen eröffnen können (dieses Problem besteht auf dem Kryptowährungsmarkt nicht). Wir mildern dies, indem wir den Handel mit Bruchteilen von Preisen reduzieren oder das Kapital erhöhen.

Schauen wir uns ein hypothetisches Beispiel an.

• Aufbau unserer Forschungsumgebung auf der Inventor Quantitative Platform

Um reibungslos arbeiten zu können, müssen wir zunächst unsere Forschungsumgebung aufbauen. In diesem Artikel verwenden wir die Inventor Quantitative Platform (FMZ.COM), um die Forschungsumgebung aufzubauen, hauptsächlich, damit wir die praktische und schnelle API nutzen können Schnittstelle und Kapselung dieser Plattform später. Komplettes Docker-System.

Im offiziellen Namen der Inventor Quantitative Platform wird dieses Docker-System als Hostsystem bezeichnet.

Weitere Informationen zum Bereitstellen von Hosts und Robotern finden Sie in meinem vorherigen Artikel: https://www.fmz.com/bbs-topic/4140

Leser, die ihren eigenen Cloud-Computing-Server-Bereitstellungshost erwerben möchten, können diesen Artikel lesen: https://www.fmz.com/bbs-topic/2848

Nach der erfolgreichen Bereitstellung des Cloud-Computing-Dienstes und des Hostsystems installieren wir das leistungsstärkste Python-Tool: Anaconda

Um alle für diesen Artikel relevanten Programmumgebungen (abhängige Bibliotheken, Versionsverwaltung etc.) zu realisieren, bietet sich am einfachsten die Verwendung von Anaconda an. Es handelt sich um ein gepacktes Python-Data-Science-Ökosystem und einen Abhängigkeitsmanager.

Informationen zur Installationsmethode von Anaconda finden Sie im offiziellen Handbuch von Anaconda: https://www.anaconda.com/distribution/

In diesem Artikel werden auch Numpy und Pandas verwendet, zwei sehr beliebte und wichtige Bibliotheken für wissenschaftliche Berechnungen mit Python.

Für die oben genannten grundlegenden Arbeiten können Sie auch meinen vorherigen Artikel lesen, in dem die Einrichtung der Anaconda-Umgebung und der beiden Bibliotheken Numpy und Pandas beschrieben wird. Weitere Einzelheiten finden Sie unter: https://www.fmz.com/digest- Thema/4169

Wir generieren zufällige Investitionen und zufällige Faktoren und ordnen sie ein. Nehmen wir an, dass unsere zukünftigen Renditen tatsächlich von diesen Faktorwerten abhängen.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

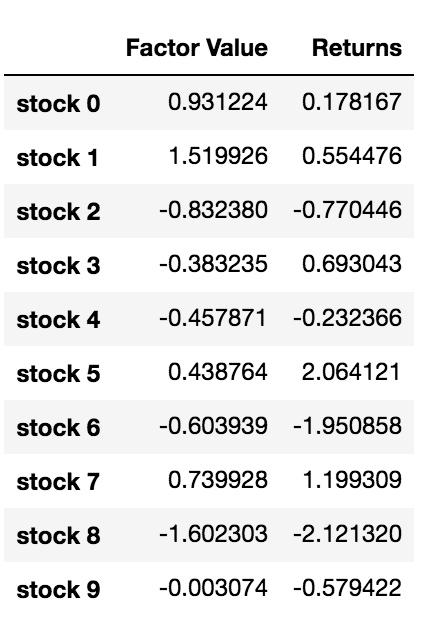
Da wir nun über Faktorwerte und Renditen verfügen, können wir sehen, was passiert, wenn wir Investitionen anhand von Faktorwerten ordnen und dann Long- und Short-Positionen eröffnen.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

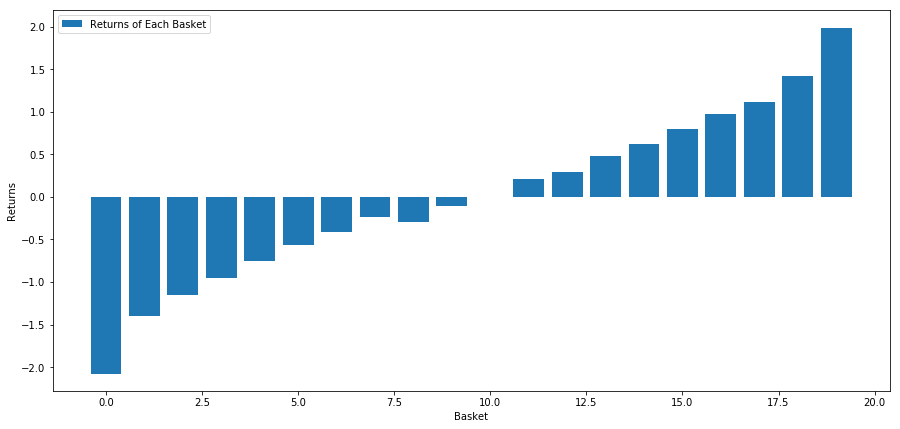
Unsere Strategie besteht darin, in einem Korb von Anlagezielen eine Long-Position bei der erstplatzierten Anlage einzunehmen und eine Short-Position beim zehntplatzierten Anlageziel einzugehen. Die Vorteile dieser Strategie sind:

basket_returns[number_of_baskets-1] - basket_returns[0]

Das Ergebnis ist: 4,172

Setzen Sie Ihr Geld auf unser Rankingmodell, um leistungsstarke von leistungsschwachen Investitionen zu unterscheiden.

Im weiteren Verlauf dieses Artikels besprechen wir die Bewertung von Rankingsystemen. Der Vorteil beim Geldverdienen mit Ranking-basierter Arbitrage besteht darin, dass man von Marktstörungen nicht betroffen ist, sondern diese ausnutzen kann.

Betrachten wir ein Beispiel aus der Praxis.

Wir laden Daten für 32 Aktien aus verschiedenen Sektoren im S&P 500 und versuchen, sie zu bewerten.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Verwenden wir den normalisierten Momentum-Indikator über einen Zeitraum von einem Monat als Grundlage für die Rangfolge

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Jetzt werden wir das Verhalten unserer Aktie analysieren und sehen, wie sich unsere Aktie im Rahmen der von uns gewählten Rankingfaktoren auf dem Markt entwickelt.

Analysieren Sie die Daten

Aktienverhalten

Sehen wir uns an, wie unser ausgewählter Aktienkorb in unserem Rankingmodell abschneidet. Berechnen wir dazu die einwöchigen Forward-Renditen für alle Aktien. Wir können dann die Korrelation der 1-Wochen-Rendite jeder Aktie mit der Dynamik der vorherigen 30 Tage betrachten. Aktien mit einer positiven Korrelation folgen dem Trend, und Aktien mit einer negativen Korrelation kehren zum Mittelwert zurück.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

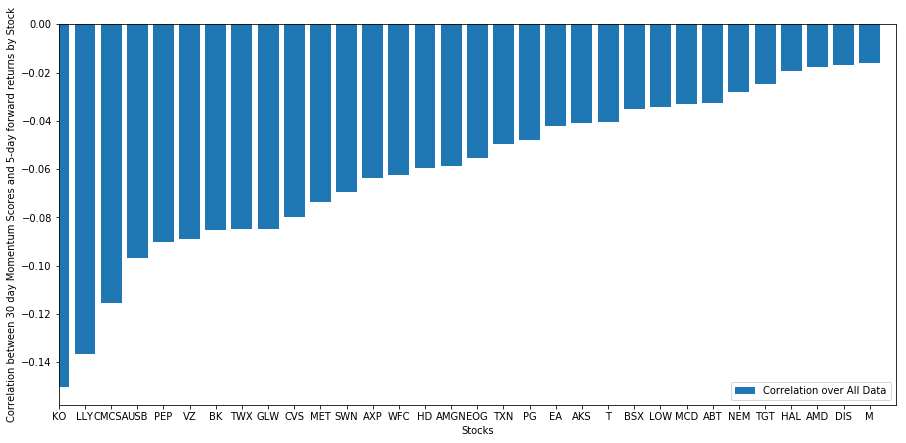
Alle unsere Aktien kehren bis zu einem gewissen Grad zum Mittelwert zurück! (Offenbar funktioniert das von uns gewählte Universum auf diese Weise.) Dies sagt uns, dass wir davon ausgehen können, dass eine Aktie, die in der Momentumanalyse einen hohen Rang einnimmt, in der nächsten Woche eine Underperformance aufweist.

Korrelation zwischen Momentum Score Ranking und Renditen

Als nächstes müssen wir uns die Korrelation zwischen unserem Ranking-Ergebnis und den zukünftigen Gesamtrenditen des Marktes ansehen, also die Beziehung zwischen der Vorhersage der erwarteten Renditen und unseren Ranking-Faktoren. Können höhere Korrelationsniveaus niedrigere relative Renditen vorhersagen oder umgekehrt?

Dazu berechnen wir die tägliche Korrelation zwischen dem 30-Tage-Momentum und den 1-Wochen-Forward-Renditen für alle Aktien.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

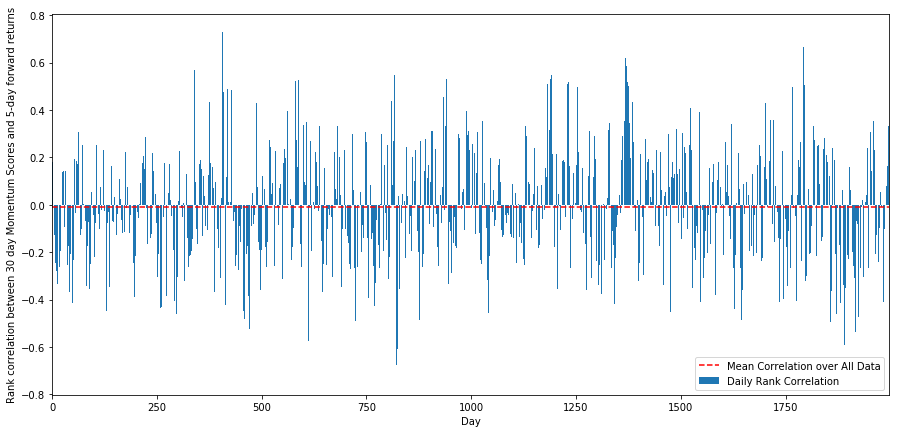
Die tägliche Korrelation ist recht unbeständig, aber sehr gering (was zu erwarten war, da wir sagten, dass alle Aktien zu ihrem Mittelwert zurückkehren werden). Wir betrachten auch die durchschnittliche monatliche Korrelation der 1-Monats-Forward-Renditen.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

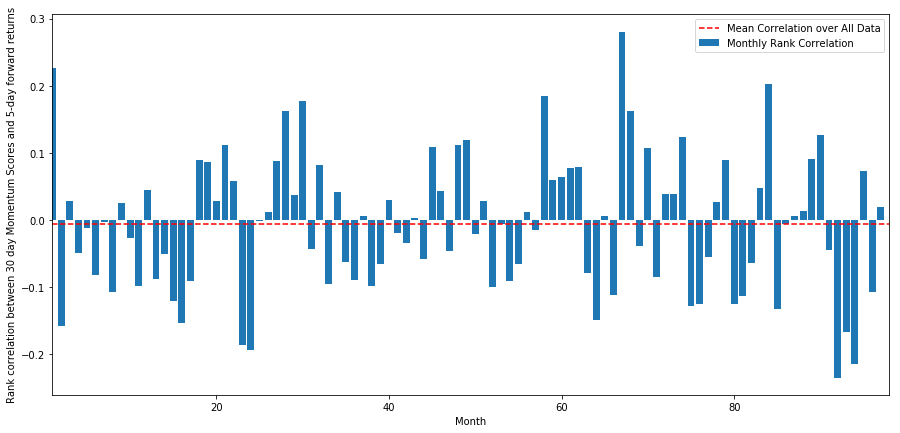
Wir sehen, dass die durchschnittliche Korrelation zwar erneut leicht negativ ist, aber auch von Monat zu Monat stark schwankt.

Durchschnittliche Aktienkorbrenditen

Wir haben die Renditen für einen Aktienkorb aus unserem Ranking berechnet. Wenn wir alle Aktien bewerten und sie dann in n Gruppen aufteilen, wie hoch ist dann die durchschnittliche Rendite jeder Gruppe?

Der erste Schritt besteht darin, eine Funktion zu erstellen, die jeden Monat den durchschnittlichen Ertrag und den Rankingfaktor für jeden Warenkorb angibt.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Wir berechnen die durchschnittliche Rendite für jeden Korb, wenn wir die Aktien auf Grundlage dieser Punktzahl einstufen. Dies sollte uns einen guten Eindruck von ihrer Beziehung über einen längeren Zeitraum hinweg geben.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

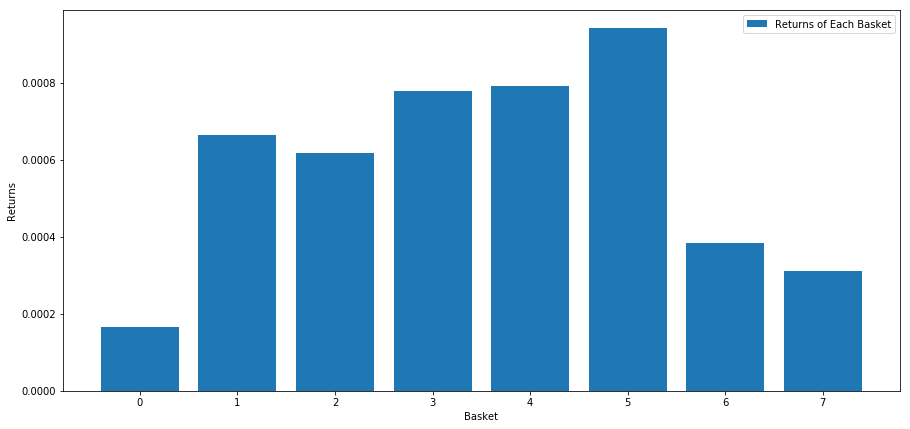
Es scheint, als könnten wir die Leistungsträger von den Leistungsschwachen trennen.

Konsistenz des Aufstrichs (Basis)

Natürlich sind dies nur durchschnittliche Beziehungen. Um zu verstehen, wie beständig die Beziehung ist und ob wir bereit sind, ein Geschäft einzugehen, sollten wir im Laufe der Zeit unsere Herangehensweise und Einstellung ihr gegenüber ändern. Als nächstes schauen wir uns ihre monatlichen Spreads (Basis) für die letzten beiden Jahre an. Wir können weitere Änderungen sehen und weitere Analysen durchführen, um zu bestimmen, ob dieser Momentum-Score handelbar ist.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

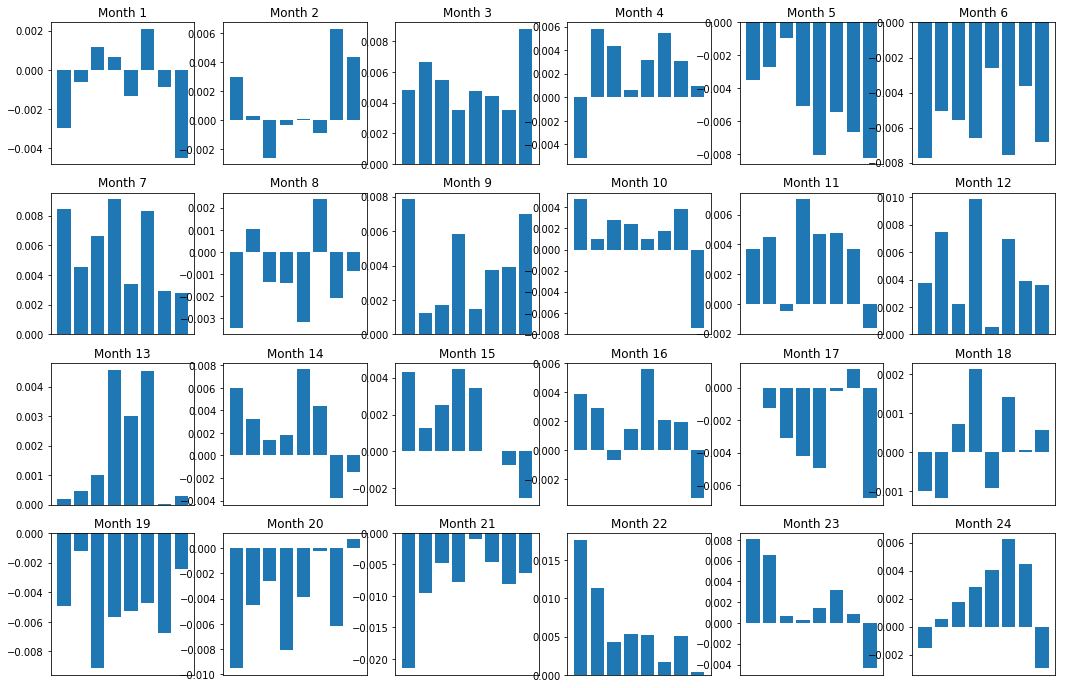
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

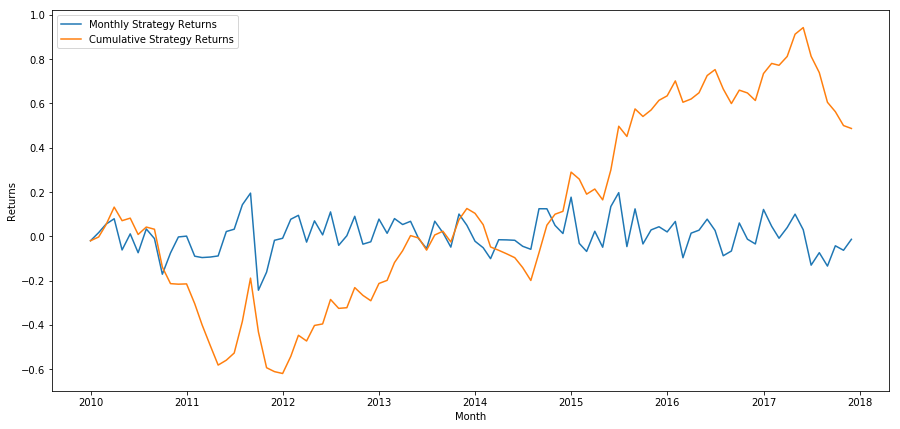
Betrachten wir abschließend die Renditen, wenn wir jeden Monat den letzten Korb long und den ersten Korb short halten (unter der Annahme einer gleichen Kapitalallokation für jedes Wertpapier).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Jährliche Rendite: 5,03 %

Wir sehen, dass wir über ein sehr schwaches Ranglistensystem verfügen, das nur mäßig zwischen Aktien mit hoher Performance und Aktien mit niedriger Performance unterscheidet. Darüber hinaus ist dieses Ranglistenschema nicht einheitlich und schwankt von Monat zu Monat erheblich.

Das richtige Ranking-Schema finden

Um eine ausgewogene Long-Short-Aktienstrategie umzusetzen, müssen Sie eigentlich nur das Rangschema festlegen. Alles danach ist mechanisch. Sobald Sie über eine ausgewogene Long-Short-Aktienstrategie verfügen, können Sie verschiedene Rankingfaktoren einfließen lassen, ohne sonst viel zu ändern. Auf diese Weise können Sie Ihre Ideen sehr bequem schnell umsetzen, ohne jedes Mal den gesamten Code optimieren zu müssen.

Auch das Rangschema kann aus nahezu jedem beliebigen Modell stammen. Es muss kein wertbasiertes Faktormodell sein, es könnte auch eine Technik des maschinellen Lernens sein, die die Renditen einen Monat im Voraus vorhersagt und sie auf dieser Grundlage bewertet.

Auswahl und Bewertung von Rankingsystemen

Das Rangschema ist der Vorteil der Long-Short-Balanced-Equity-Strategie und zugleich der wichtigste Baustein. Die Auswahl eines guten Ranking-Schemas ist ein systematisches Projekt und es gibt keine einfachen Antworten.

Ein guter Ausgangspunkt besteht darin, vorhandene bekannte Technologien auszuwählen und zu prüfen, ob Sie sie leicht modifizieren können, um höhere Erträge zu erzielen. Wir besprechen hier einige Ansatzpunkte:

• Klonen und anpassen: Suchen Sie sich etwas aus, das oft diskutiert wird, und prüfen Sie, ob Sie es zu Ihrem Vorteil leicht abändern können. Typischerweise verfügen öffentliche Faktoren über keine Handelssignale mehr, da sie durch Arbitrage vollständig aus dem Markt verdrängt wurden. Manchmal können sie Sie jedoch in die richtige Richtung lenken.

• Preismodell: Jedes Modell, das zukünftige Renditen vorhersagt, kann ein Faktor sein und potenziell zur Bewertung Ihres Korbs von Handelszielen verwendet werden. Sie können jedes komplexe Preismodell nehmen und es in ein Ranking-Schema umwandeln.

• Preisbasierte Faktoren (technische Indikatoren): Preisbasierte Faktoren, wie die, die wir heute besprochen haben, verwenden Informationen über den historischen Preis jeder Aktie und generieren daraus einen Faktorwert. Beispiele könnten gleitende Durchschnittsindikatoren, Momentumindikatoren oder Volatilitätsindikatoren sein.

• Regression und Momentum: Es ist erwähnenswert, dass einige Faktoren davon ausgehen, dass sich die Preise, wenn sie sich einmal in eine Richtung bewegt haben, auch weiterhin in diese Richtung bewegen werden. Bei manchen Faktoren ist das genaue Gegenteil der Fall. Beide sind gültige Modelle für unterschiedliche Zeitrahmen und Vermögenswerte und es ist wichtig zu untersuchen, ob das zugrunde liegende Verhalten auf Dynamik oder Regression basiert.

• Fundamentale Faktoren (wertbasiert): Hierbei wird eine Kombination aus fundamentalen Werten wie KGV, Dividenden etc. verwendet. Der Fundamentalwert enthält Informationen zu realen Fakten über ein Unternehmen und kann daher in vielerlei Hinsicht aussagekräftiger sein als der Preis.

Letztlich ist die Entwicklung von Prädiktoren ein Wettrüsten, bei dem man versucht, immer einen Schritt voraus zu sein. Faktoren werden durch Arbitrage aus dem Markt genommen und haben eine begrenzte Lebensdauer. Sie müssen daher kontinuierlich daran arbeiten, den Grad des Verfalls Ihrer Faktoren zu ermitteln und festzustellen, welche neuen Faktoren sie ersetzen können.

Weitere Überlegungen

• Häufigkeit der Neugewichtung

Jedes Rankingsystem prognostiziert Erträge über einen leicht unterschiedlichen Zeitraum. Eine preisbasierte Rückkehr zum Mittelwert kann möglicherweise über einen Zeitraum von einigen Tagen eine Vorhersage ermöglichen, während wertbasierte Faktormodelle möglicherweise über einen Zeitraum von einigen Monaten eine Vorhersage ermöglichen. Es ist sehr wichtig, den Zeithorizont zu bestimmen, für den das Modell Prognosen erstellen soll, und diesen vor der Ausführung der Strategie statistisch zu validieren. Sie möchten sicher nicht überanpassen, indem Sie versuchen, Ihre Neugewichtungsfrequenz zu optimieren; Sie werden unweigerlich eine finden, die zufällig die anderen übertrifft. Sobald Sie den Zeithorizont bestimmt haben, den Ihr Ranking-Schema vorhersagt, versuchen Sie, ungefähr in dieser Frequenz neu zu gewichten, um Holen Sie das Beste aus Ihrem Modell heraus.

• Kapitalkapazität und Transaktionskosten

Für jede Strategie gelten Mindest- und Höchstkapitalanforderungen, wobei die Mindestschwelle üblicherweise durch die Transaktionskosten bestimmt wird.

Der Handel mit zu vielen Aktien führt zu hohen Transaktionskosten. Angenommen, Sie möchten 1.000 Aktien kaufen, dann entstehen Ihnen für jede Umschichtung Kosten von mehreren Tausend Dollar. Ihre Kapitalbasis muss so hoch sein, dass die Transaktionskosten nur einen kleinen Bruchteil der durch Ihre Strategie erzielten Erträge ausmachen. Wenn Ihr Kapital beispielsweise 100.000 US-Dollar beträgt und Sie mit Ihrer Strategie 1 % (1.000 US-Dollar) pro Monat erwirtschaften, wird dieser gesamte Ertrag durch die Transaktionskosten aufgezehrt. Um mit dieser Strategie einen Gewinn von mehr als 1.000 Aktien zu erzielen, bräuchten Sie Kapital in Millionenhöhe.

Die Höhe des Mindestvermögens richtet sich maßgeblich nach der Anzahl der gehandelten Aktien. Allerdings ist auch die maximale Kapazität sehr hoch und mit Long-Short-Balanced-Equity-Strategien lassen sich Hunderte Millionen Dollar handeln, ohne ihren Vorteil zu verlieren. Dies ist der Fall, weil die Strategie relativ selten neu gewichtet wird. Der Gesamtvermögenswert geteilt durch die Anzahl der gehandelten Aktien ergibt einen sehr niedrigen Dollarwert pro Aktie und Sie müssen sich keine Sorgen machen, dass Ihr Handelsvolumen den Markt bewegt. Nehmen wir an, Sie handeln mit 1.000 Aktien, das sind 100.000.000 $. Wenn Sie Ihr gesamtes Portfolio jeden Monat neu ausbalancieren würden, würden Sie pro Aktie nur 100.000 US-Dollar pro Monat handeln, was für die meisten Wertpapiere nicht ausreicht, um einen signifikanten Marktanteil zu erreichen.