Parlons de la façon d’optimiser les paramètres de plusieurs modèles de trading programmatique

• #### Hauteur paramétrique et île paramétrique

　 Un principe important dans l’optimisation des paramètres est de rechercher des plateaux de paramètres plutôt que des îlots de paramètres. Les plateaux de paramètres signifient qu’il existe une plage de paramètres plus large dans laquelle les modèles obtiennent de meilleurs résultats.

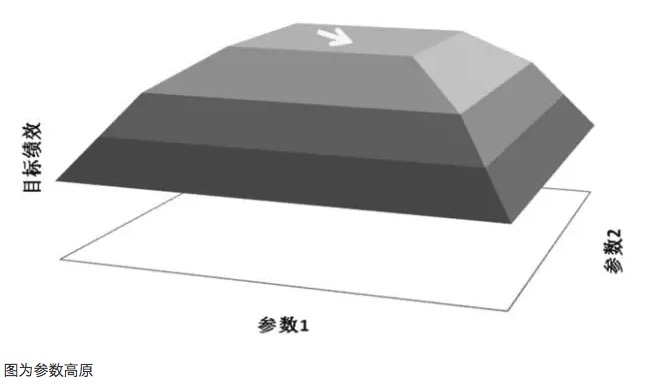
• #### Le plateau paramétrable

Par exemple, si un modèle de transaction contient deux paramètres, respectivement paramètre 1 et paramètre 2, un diagramme de performance en trois dimensions est obtenu après un test de traversée des deux paramètres. Une bonne distribution des paramètres devrait être un diagramme de hauteur des paramètres, et la performance du modèle est garantie, même si les paramètres sont décalés.

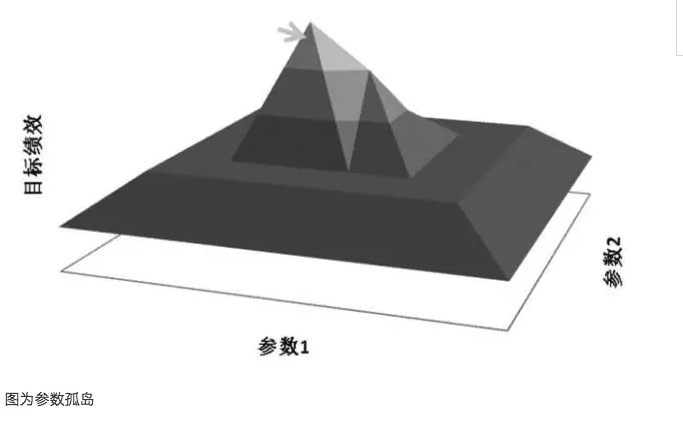
Généralement, si la performance d’un système de paramètres proches est bien inférieure à celle d’un paramètre optimal, alors ce paramètre optimal est probablement le résultat d’une surestimation et peut être considéré mathématiquement comme une solution singulière, plutôt que la solution de valeur maximale recherchée. D’un point de vue mathématique, la singularité est instable et, dans un contexte d’incertitude future, le paramètre optimal peut devenir le paramètre le plus défavorable une fois que les caractéristiques du marché changent.

L’hyperadaptation est liée à l’échantillon choisi. Si l’échantillon choisi ne peut pas représenter la caractéristique globale du marché, il suffit d’ajuster les paramètres pour que les résultats des tests atteignent la valeur attendue positive, ce qui est sans aucun doute de l’auto-illusion. Les paramètres obtenus sont les paramètres inefficaces de l’hyperadaptation.

La principale contradiction entre la suradaptation et l’optimisation paramétrique est que les paramètres optimaux obtenus par l’optimisation des paramètres du modèle ne sont basés que sur des échantillons de données historiques qui ont déjà eu lieu, tandis que les événements futurs changent dynamiquement, avec des similitudes et des variations par rapport aux événements historiques. Les concepteurs de modèles peuvent trouver les paramètres du modèle qui ont été les meilleurs dans l’histoire, mais ce paramètre n’est pas nécessairement le meilleur dans les applications réelles du modèle futur, et encore moins le meilleur paramètre du modèle historique, qui peut être un paramètre qui se comporte mal dans les batailles de modèles futurs, voire entraîner des pertes importantes. Par exemple, le choix d’un paramètre qui capte une grande vague d’événements historiques, mais la définition d’une telle valeur paramétrique ne signifie pas que le modèle se comportera aussi bien dans les batailles futures.

En outre, les plateaux paramétriques et les îles paramétriques ont souvent une relation plus étroite avec le nombre de transactions. Si le nombre de transactions du modèle est inférieur, il est souvent possible de trouver un point de paramètres approprié, ce qui rend le modèle rentable sur ces transactions.

• #### Méthode pour optimiser les paramètres

Une fois que l’on connaît les plateaux paramétriques et les îles paramétriques, il est important d’optimiser les paramètres, en particulier lorsque plusieurs paramètres sont présents dans le modèle (appelé l’arrayon paramétrique), car la prise de valeur d’un paramètre affecte souvent la distribution des plateaux d’un autre paramètre. Alors, comment optimiser l’arrayon paramétrique?

Une méthode est la convergence progressive: on optimise d’abord un paramètre individuellement, puis on fixe l’optimisation sur un autre paramètre, puis on fixe l’optimisation sur l’autre paramètre, et ainsi de suite jusqu’à ce que le résultat de l’optimisation ne change plus. Par exemple, dans un modèle de négociation linéaire homogène, deux paramètres indépendants sont respectivement le cycle moyen court N1 et le cycle long N2. On fixe d’abord N2 comme 1, on fait un filtrage de test sur N1 dans une plage de valeurs allant de 1 à 100 pour trouver le meilleur résultat, qui est finalement fixé à 8; ensuite, on optimise N2 entre 1 et 200 pour obtenir le meilleur résultat, qui est fixé à 26; une deuxième fois encore, on effectue un deuxième tour d’optimisation sur N1 pour obtenir le nouveau meilleur résultat, qui est fixé à 10; enfin, on optimise N2 pour obtenir le meilleur résultat, qui est finalement fixé à 28; et ainsi de suite à la sélection cyclique,

Une autre méthode consiste à utiliser une plate-forme de conception de logiciels programmatiques dotée de puissantes fonctionnalités de calcul, à calculer directement la distribution entre la fonction cible et l’arrangement de paramètres, puis à rechercher la distribution de la différence multidimensionnelle, à définir un seuil de différence dont la valeur absolue de différence est inférieure à la valeur de seuil correspondant à la plus grande taille multidimensionnelle, le plus haut rayon de coupe multidimensionnel, sélectionné comme la valeur de paramètre la plus stable.

En plus de la méthode d’optimisation des paramètres, l’échantillonnage des données est également un facteur important. Les modèles qui suivent la tendance comme idée de négociation fonctionnent mieux en cas de tendance, tandis que les stratégies qui négocient des idées de vente à bas prix et de vente à prix élevé fonctionnent mieux en cas d’oscillation. Par conséquent, lors de l’optimisation des paramètres, il est nécessaire d’éliminer de manière appropriée les tendances qui correspondent à l’idée de négociation pour considérer les profits et d’ajouter des données sur les tendances qui ne correspondent pas à la stratégie pour considérer les pertes.

Si l’on prend l’exemple de l’indice boursier à terme, le premier jour de sa mise en bourse en 2010 et la seconde moitié de l’année 2014 qui a vu l’apparition d’une situation de bull market extrême, l’indice boursier à terme est un marché à sens unique. Il ne fait aucun doute que tous les modèles de tendance obtiennent de bons résultats. Cependant, si nous intégrons ces données de tendance extrême dans l’échantillon pour optimiser les paramètres, les paramètres du modèle obtenus ne sont pas nécessairement les meilleurs.

Par exemple, supposons qu’un modèle possède deux paramètres: le paramètre A est testé très bien pour une période de temps unilatérale, et fonctionne normalement pour les autres périodes; un autre paramètre B est testé moins bien pour une période de temps unilatérale que le paramètre A, et fonctionne mieux pour les autres périodes, et la répartition entre les périodes est uniforme par rapport au paramètre A. Même si le paramètre A est testé pour des indicateurs synthétiques tels que le bénéfice-risque supérieur au paramètre B dans l’ensemble des données de l’échantillon, nous sommes plus enclins à choisir le paramètre B, car le paramètre B est relativement plus stable et n’est pas dépendant d’un échantillon particulier.

En résumé, lors de la construction d’un modèle de transaction programmatique, il est possible d’améliorer le modèle par l’optimisation des paramètres, de sorte que le modèle s’adapte mieux aux modèles de fluctuation des prix et augmente le rendement des investissements. D’autre part, il est nécessaire d’éviter une adaptation excessive à l’optimisation des paramètres, ce qui réduit considérablement l’adaptabilité du modèle aux changements de marché.

Il y a des gens qui ne sont pas d’accord avec moi.