आइए बात करते हैं कि कई प्रोग्रामेटिक ट्रेडिंग मॉडल के मापदंडों को कैसे अनुकूलित किया जाए

• #### पैरामीटर उच्चभूमि और पैरामीटर द्वीप

　 पैरामीटर अनुकूलन में एक महत्वपूर्ण सिद्धांत है कि पैरामीटर के लिए लड़ने के लिए उच्च क्षेत्र नहीं है पैरामीटर द्वीप. तथाकथित पैरामीटर उच्च क्षेत्र, का अर्थ है कि वहाँ एक व्यापक पैरामीटर रेंज है, मॉडल इस पैरामीटर के दायरे में बेहतर प्रभाव प्राप्त कर सकते हैं, आम तौर पर उच्च क्षेत्र के केंद्र के साथ लगभग सामान्य वितरण का गठन. तथाकथित पैरामीटर द्वीप, का अर्थ है कि केवल जब पैरामीटर मान एक बहुत ही छोटी सीमा में है, मॉडल का अच्छा प्रदर्शन है, और जब पैरामीटर इस मूल्य से विचलित होते हैं, तो मॉडल का प्रदर्शन स्पष्ट रूप से बदल जाता है।

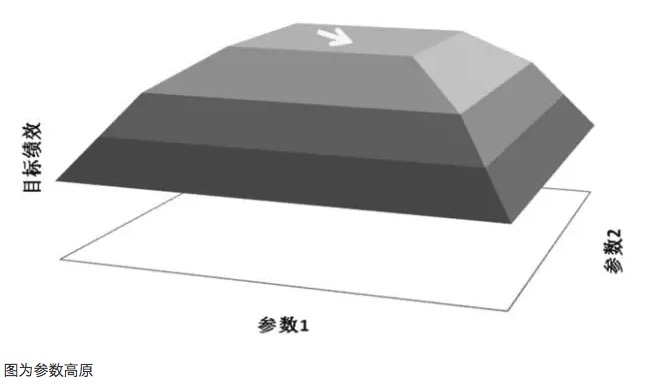
• #### ऊंचाई

उदाहरण के लिए, मान लीजिए कि एक ट्रेडिंग मॉडल में दो पैरामीटर हैं, पैरामीटर 1 और पैरामीटर 2, और जब दोनों पैरामीटरों का क्रॉस-टेस्ट किया जाता है, तो एक त्रि-आयामी प्रदर्शन चार्ट प्राप्त होता है। अच्छा पैरामीटर वितरण पैरामीटर के उच्च स्थान का इरादा होना चाहिए, यहां तक कि जब पैरामीटर की सेटिंग विचलित हो जाती है, तो मॉडल का लाभप्रद प्रदर्शन अभी भी सुनिश्चित किया जा सकता है। इस तरह के पैरामीटर की स्थिरता मजबूत हो सकती है, जिससे मॉडल को भविष्य में वास्तविक जीवन में विभिन्न प्रकार की स्थितियों का सामना करने के लिए मजबूत प्रतिक्रियाशीलता हो सकती है। लेकिन यदि पैरामीटर के बाद के पैरामीटर का प्रदर्शन, जैसे कि पैरामीटर आइलैंड्स का इरादा, जब पैरामीटर का छोटा विचलन होता है, तो मॉडल का लाभप्रदता बहुत बदल जाता है, तो पैरामीटर का अनुकूलीकरण प्रदर्शन खराब होता है, जो अक्सर वास्तविक व्यापार में परिवर्तनशील बाजार की स्थिति का सामना करना मुश्किल होता है।

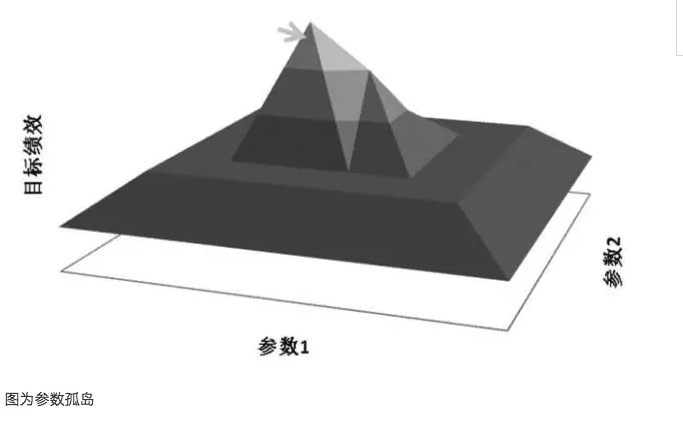
आम तौर पर, यदि निकटवर्ती पैरामीटर प्रणाली की क्षमता सबसे अच्छा पैरामीटर की क्षमता से बहुत अलग है, तो यह सबसे अच्छा पैरामीटर एक अति-समीकरण का परिणाम हो सकता है, जिसे गणितीय रूप से अनन्य समाधान के रूप में माना जा सकता है, न कि खोज करने के लिए सबसे बड़ा मूल्य समाधान। गणितीय रूप से, एक अनन्यता अस्थिर है, और भविष्य की अनिश्चितता में, एक बार बाजार की विशेषताएं बदल जाती हैं, सबसे अच्छा पैरामीटर सबसे खराब पैरामीटर में बदल सकता है।

ओवरफिट चयनित नमूने से संबंधित है, यदि चयनित नमूना बाजार की समग्र विशेषता का प्रतिनिधित्व नहीं करता है, तो केवल परीक्षण के परिणाम को सकारात्मक अपेक्षित मूल्य तक पहुंचाने के लिए पैरामीटर को समायोजित करने के लिए, यह निश्चित रूप से आत्म-धोखाधड़ी है, जो पैरामीटर का मूल्य है जो ओवरफिट के अप्रभावी पैरामीटर का मूल्य है। उदाहरण के लिए, पैरामीटर ओवरफिट का विश्लेषण करके, ट्रेडिंग मॉडल में क्रमशः 35 और 63 के मानों पर रिटर्न की वृद्धि होती है। यदि मॉडल में संबंधित संकेतक 35 और 63 को पैरामीटर के रूप में चुना जाता है, तो मॉडल का रिटर्न बहुत अच्छा लगता है, लेकिन वास्तव में यह एक विशिष्ट पैरामीटर आइसलैंड प्रभाव है।

अति-फिट और पैरामीटर अनुकूलन के बीच मुख्य विरोधाभास यह है कि मॉडल पैरामीटर अनुकूलन के लिए सबसे अच्छा पैरामीटर केवल ऐतिहासिक डेटा के नमूने पर आधारित है जो पहले से ही हो चुका है, जबकि भविष्य में व्यवहार गतिशील परिवर्तनशील है, जो ऐतिहासिक व्यवहार की तुलना में समानता और भिन्नता दोनों है। मॉडल डिजाइनर मॉडल को ऐतिहासिक रूप से सबसे अच्छा प्रदर्शन करने वाले पैरामीटर पा सकते हैं, लेकिन यह पैरामीटर भविष्य के मॉडल के वास्तविक अनुप्रयोगों में सबसे अच्छा प्रदर्शन नहीं करता है, और इससे भी अधिक ऐतिहासिक रूप से सबसे अच्छा प्रदर्शन करने वाले मॉडल पैरामीटर, भविष्य के मॉडल वास्तविक युद्धों में खराब प्रदर्शन करने वाले पैरामीटर हो सकते हैं, यहां तक कि भारी नुकसान भी। उदाहरण के लिए, एक पैरामीटर को चुना गया है जो इतिहास में एक बड़ी लहर को पकड़ सकता है, लेकिन इस तरह के पैरामीटर मानों के साथ एक मॉडल को सेट करना इसका मतलब यह नहीं है कि मॉडल भविष्य के युद्धों में भी इतना अच्छा प्रदर्शन कर सकता है।

इसके अलावा, पैरामीटर हाइलाइट्स और पैरामीटर आइलैंड्स अक्सर लेनदेन की संख्या के साथ अधिक संबंध रखते हैं। यदि मॉडल के लेनदेन की संख्या कम है, तो अक्सर एक उपयुक्त पैरामीटर बिंदु पाया जा सकता है, जिससे मॉडल इन कई लेनदेन में लाभान्वित हो जाता है। इस पैरामीटर के अनुकूलन के बाद मॉडल लाभप्रदता मजबूत आकस्मिकता को दर्शाती है। यदि मॉडल के लेनदेन की संख्या अधिक है, तो मॉडल लाभप्रदता की आकस्मिकता कम हो जाएगी, और लाभप्रदता की अनिवार्यता और नियमितता को दर्शाती है, तो एक पैरामीटर हाइलाइट भी होगा। इस प्रकार के पैरामीटर अनुकूलन मॉडल में पैरामीटर अनुकूलन का उद्देश्य है।

• #### पैरामीटर अनुकूलित करने के लिए विधि

एक बार जब हम पैरामीटर के उच्च क्षेत्र और पैरामीटर द्वीपों को समझ लेते हैं, तो पैरामीटर को अनुकूलित करने के तरीके महत्वपूर्ण हो जाते हैं, खासकर जब मॉडल में कई पैरामीटर होते हैं (जैसे कि पैरामीटर सरणी), अक्सर एक पैरामीटर का मान लेने से दूसरे पैरामीटर के उच्च क्षेत्र का वितरण प्रभावित होता है। तो पैरामीटर सरणी का अनुकूलन कैसे करें?

एक विधि है चरणबद्ध समापन विधि। अर्थात्, पहले एक पैरामीटर को व्यक्तिगत रूप से अनुकूलित किया जाता है, उसके सर्वोत्तम मूल्य को प्राप्त करने के बाद इसे स्थिर किया जाता है, और फिर दूसरे पैरामीटर को अनुकूलित किया जाता है, उसके सर्वोत्तम मूल्य को प्राप्त करने के बाद इसे स्थिर किया जाता है। इस तरह से चक्र, जब तक कि अनुकूलन परिणाम नहीं बदलता है। उदाहरण के लिए, एक रैखिक क्रॉस-बिक्री व्यापार मॉडल, दो स्वतंत्र पैरामीटर औसत लघु अवधि N1 और लंबी अवधि N2 हैं। पहले N2 को 1 के रूप में निर्धारित किया गया है, N1 को 1 से 100 के मानों की सीमा में परीक्षण के लिए चुना गया है, और अंतिम सर्वोत्तम मूल्य 8 के रूप में चुना गया है; फिर N2 को 1 से 200 के बीच अनुकूलित किया गया है, 26 के रूप में चुना गया है; फिर से N1 के लिए दूसरे दौर का अनुकूलन किया गया है, 10 के नए मानों के रूप में चुना गया है, और अंतिम रूप से N2 के लिए अनुकूलन किया गया है, 28 के रूप में चुना गया है। और इस तरह के चक्र का चयन किया जाता है, जब तक कि अनुकूलन परिणाम नहीं बदलता है। यदि अंतिम पैरा

एक अन्य तरीका यह है कि एक प्रोग्रामेटिक सॉफ्टवेयर डिजाइन प्लेटफॉर्म का उपयोग करें जिसमें मजबूत कंप्यूटिंग क्षमता हो, सीधे लक्ष्य फ़ंक्शन और पैरामीटर सरणी के बीच वितरण की गणना करें, और फिर बहु-आयामी अंतर के वितरण की खोज करें, एक अंतर थ्रेशोल्ड को परिभाषित करें, जिसमें अंतर पूर्ण मूल्य थ्रेशोल्ड रेंज से कम है। सबसे बड़ा बहु-आयामी आकार, सबसे बड़ा बहु-आयामी इंट्रा-स्लाइड त्रिज्या, सबसे स्थिर पैरामीटर मान के रूप में चुना गया है।

पैरामीटर अनुकूलन के अलावा, डेटा नमूनाकरण भी एक महत्वपूर्ण कारक है। ट्रेडिंग विचार के रूप में ट्रेंड-ट्रेसिंग मॉडल ट्रेंड के दौरान बेहतर प्रदर्शन करते हैं, और ट्रेडिंग विचार के रूप में उच्च-बिक्री-निम्न-खरीद की रणनीति उतार-चढ़ाव के दौरान बेहतर प्रदर्शन करती है। इसलिए, पैरामीटर अनुकूलन में, लाभ के लिए ट्रेडिंग विचार के अनुरूप व्यवहार को ठीक से हटाने की आवश्यकता होती है, और ट्रेडिंग विचार के अनुरूप नहीं होने वाले व्यवहार डेटा को नुकसान के लिए जोड़ना होता है।

उदाहरण के लिए, स्टॉक इंडेक्स फ्यूचर्स, स्टॉक इंडेक्स फ्यूचर्स एकतरफा हैं, जो 2010 में शुरू हुए थे और 2014 के उत्तरार्ध में जब चरम बैल बाजार की स्थिति उत्पन्न हुई थी। इसमें कोई संदेह नहीं है कि सभी प्रवृत्ति मॉडल अच्छे परिणाम देंगे। हालांकि, यदि हम इस चरम प्रवृत्ति डेटा को भी नमूने में पैरामीटर अनुकूलन के लिए डालते हैं, तो प्राप्त मॉडल पैरामीटर सबसे अच्छे नहीं होंगे।

उदाहरण के लिए, मान लीजिए कि एक मॉडल में दो पैरामीटर हैं, पैरामीटर ए का परीक्षण परिणाम एकतरफा घटना के समय में बहुत अच्छा है, अन्य समय में सामान्य प्रदर्शन; एक अन्य पैरामीटर बी का परीक्षण परिणाम एकतरफा घटना के समय में पैरामीटर ए से कम है, अन्य समय में बेहतर प्रदर्शन, प्रत्येक समय के बीच वितरण पैरामीटर ए के बराबर है। यहां तक कि अगर पैरामीटर ए पूरे नमूने के डेटा में परीक्षण किए गए समग्र संकेतकों जैसे कि जोखिम-लाभ पैरामीटर बी से अधिक है, तो हम पैरामीटर बी का चयन करने के लिए अधिक इच्छुक हैं, क्योंकि पैरामीटर बी अपेक्षाकृत अधिक स्थिर है और किसी विशेष नमूने पर निर्भर नहीं है।

संक्षेप में, जब एक प्रोग्रामेटिक ट्रेडिंग मॉडल का निर्माण किया जाता है, तो एक ओर, मॉडल को पैरामीटर अनुकूलन के माध्यम से बेहतर बनाया जा सकता है, ताकि मॉडल कीमतों में उतार-चढ़ाव के पैटर्न के लिए बेहतर रूप से अनुकूल हो सके, जिससे निवेश पर रिटर्न बढ़ सके; दूसरी ओर, पैरामीटर अनुकूलन के लिए अति-फिट को रोकना, जिससे मॉडल की अनुकूलता में भारी कमी हो।

प्रोग्रामेटिक ट्रेडर