Regresi linier - metode kuadrat terkecil

• ### 1. Pengantar

Pada saat itu, saya belajar matematika mesin, dan saya merasa cukup sulit untuk mempelajari Logistic Regression di Bab 5. Saya menelusuri kembali dari Logistic Regression ke Linear Regression, dan kemudian ke Minimum Dua Perkalian. Akhirnya, saya masuk ke Matematika Tingkat Tinggi, Bab IX, Bagian 10 dari Minimum Dua Perkalian, dan saya tahu dari mana prinsip matematika di balik Minimum Dua Perkalian. Paduan minimal dua kali lipat adalah salah satu implementasi dari rumus empiris dalam masalah optimasi. Pemahaman tentang prinsip-prinsipnya akan berguna untuk memahami Paduan Regressi Logistik dan Paduan Pembelajaran Paduan untuk mendukung mesin vektor.

• ### Kedua, pengetahuan latar belakang

Latar belakang sejarah munculnya pecahan kecil dua kali ganda adalah sangat menarik.

Pada tahun 1801, astronom Italia Giuseppe Piazzi menemukan asteroid pertama, Ceres. Setelah 40 hari pengamatan, Piazzi kehilangan posisi Ceres karena Ceres berjalan ke belakang Matahari. Kemudian, para ilmuwan di seluruh dunia menggunakan data pengamatan Piazzi untuk mencari Ceres, tetapi tidak ada hasil berdasarkan hasil yang dihitung oleh kebanyakan orang. Gauss, yang saat itu berusia 24 tahun, juga menghitung orbit Ceres.

Metode yang digunakan Gauss untuk perkalian dua terkecil dipublikasikan dalam bukunya pada tahun 1809 tentang teori gerak benda-benda langit, dan ilmuwan Prancis Lejeune menemukan perkalian dua terkecil secara independen pada tahun 1806, tetapi diam-diam tidak diketahui karena tidak diketahui oleh orang-orang pada saat itu. Kedua orang tersebut pernah berselisih tentang siapa yang pertama kali menciptakan prinsip perkalian dua terkecil.

Pada tahun 1829, Gauss memberikan bukti bahwa efek optimasi dari perkalian dua terkecil lebih kuat daripada metode lain, lihat Teorema Gauss-Markov.

• ### Ketiga, penggunaan pengetahuan

Inti dari rumus ini adalah untuk menjamin semua data yang menyimpang dari kuadrat dan minimum.

Jika kita mengumpulkan data panjang dan lebar dari beberapa kapal perang,

Dari data tersebut, kami menggambar peta titik-titik pada Python:

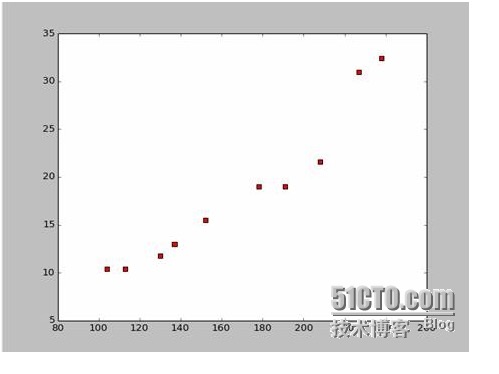
Kode untuk menggambar peta titik-titik adalah sebagai berikut:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Jika kita ambil dua titik pertama, 238, 32, 4, 152, 15, 5, kita akan mendapatkan dua persamaan. 152*a+b=15.5 328*a+b=32.4 Jadi kita bisa mendapatkan a = 0,197 dan b = -14,48. Jadi, kita bisa mendapatkan gambar yang mirip seperti ini:

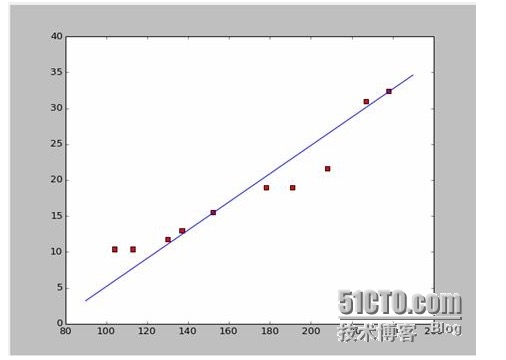
Baiklah, sekarang ada pertanyaan baru, apakah a dan b adalah solusi optimal? Jika kita berbicara secara profesional, apakah a dan b adalah parameter optimal dari model? Sebelum menjawab pertanyaan ini, kita harus menjawab pertanyaan lain:

Jawabannya adalah: untuk menjamin bahwa semua data akan menyimpang dari kuadrat dan minimum. Untuk prinsipnya, kita akan membahas di kemudian hari, kita akan melihat bagaimana menggunakan alat ini untuk menghitung a dan b terbaik. Dengan asumsi bahwa semua data akan menyimpang dari kuadrat dan minimum.

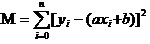
Sekarang kita akan mencari a dan b terkecil dari M. Perhatikan bahwa dalam persamaan ini kita sudah tahu y dan xi.

Jadi persamaan ini adalah sebuah fungsi biner dengan a, b sebagai variabelnya sendiri dan M sebagai variabelnya sendiri.

Ingatlah bagaimana fungsi satuan pada bilangan tinggi memiliki nilai ekstrim. Kita menggunakan derivatif sebagai alat. Pada fungsi biner, kita masih menggunakan derivatif. Hanya saja derivatif di sini memiliki nama baru yaitu derivatif bias. Dengan mencari derivatif dari M, kita mendapatkan sebuah himpunan persamaan.

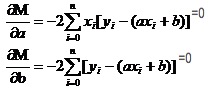
Dalam kedua persamaan ini, x dan y diketahui.

Karena data yang digunakan berasal dari Wikipedia, saya akan langsung menggunakan jawaban untuk menggambar gambar yang cocok:

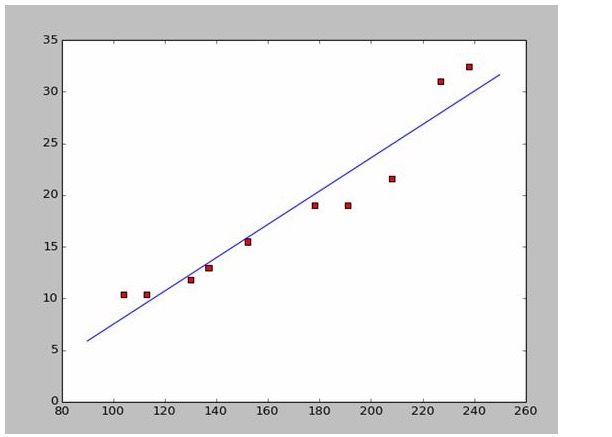
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Empat Prinsip Pencarian

Dalam pencocokan data, mengapa kita mengoptimalkan parameter model dengan memaksimalkan nilai mutlak dan minimum dari perkalian kuadrat dari prediksi model dengan data aktual?

Pertanyaan ini telah dijawab, lihat link https://blog.sciencenet.cn/blog-430956-621997.html

Secara pribadi saya merasa bahwa penjelasan ini sangat menarik. Terutama asumsi di dalamnya: semua titik yang menyimpang dari f (x) adalah berisik.

Semakin jauh suatu titik dari titik yang dimaksud, maka semakin besar kebisingan yang terjadi, maka semakin kecil pula kemungkinan terjadinya titik tersebut. Lalu, apa hubungannya tingkat penyimpangan x dengan probabilitas terjadinya f (x)?

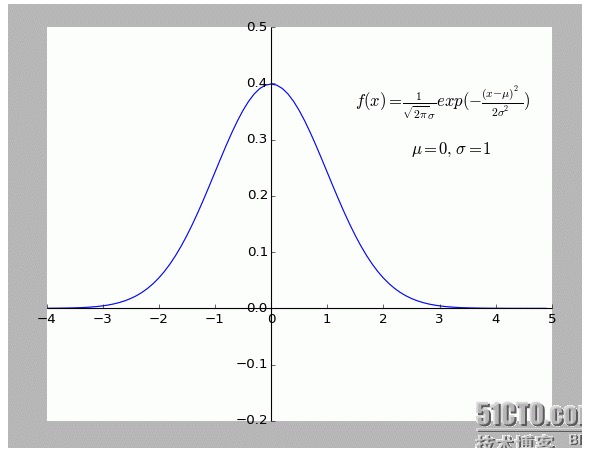
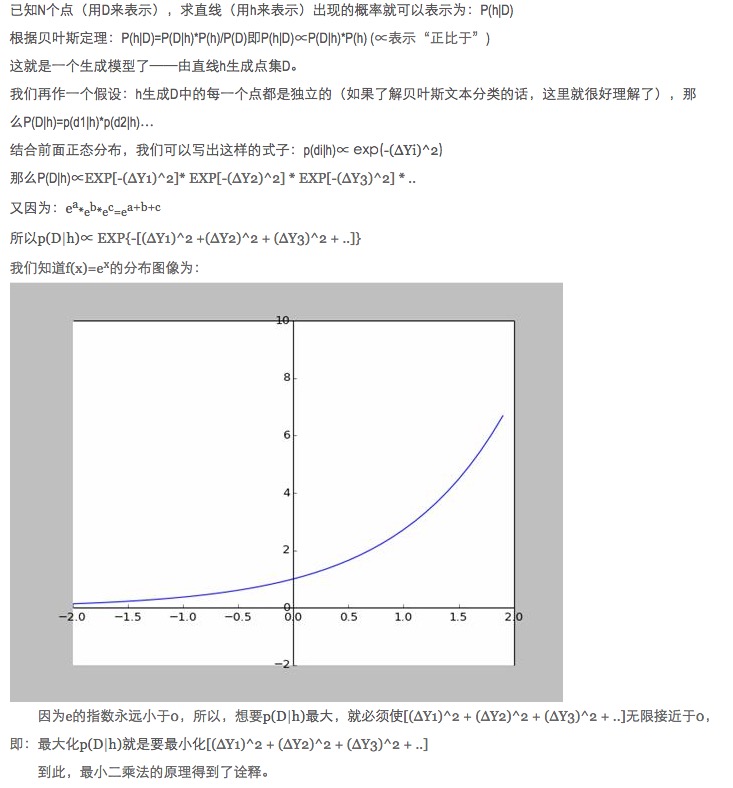
• ### Lima, memperluas.

Yang disebutkan di atas adalah situasi dua dimensi, yaitu hanya ada satu variabel diri. Tetapi di dunia nyata yang mempengaruhi hasil akhir adalah superposisi dari berbagai faktor, yaitu variabel diri akan memiliki beberapa situasi.

Untuk fungsi metalineral N umum, menggunakan matriks terbalik dalam silinder aljabar linier untuk mencari solusi sudah OK; karena tidak ada contoh yang cocok untuk sementara waktu, hanya sebagai sebuah argumen, tinggal di sini.

Tentu saja, alam lebih dari sekedar kesesuaian polimer, bukan kesesuaian linear, yang merupakan hal yang lebih tinggi.

• Referensi

  • Perpustakaan Matematika Tinggi (Edisi Keenam)
  • Aljabar linier (Publikasi Universitas Peking)
  • Saya tidak tahu apa yang harus saya lakukan.Minimal dua kali lipat
  • Wikipedia: Perkalian dua terkecil
  • Jaringan Sains:Minimal dua kali lipat?

Karya asli, izin untuk dipublikasikan, dipublikasikan dengan hyperlink yang menandai sumber asli artikel, informasi penulis dan pernyataan ini. Jika tidak, Anda akan bertanggung jawab secara hukum. http://sbp810050504.blog.51cto.com/2799422/1269572