前回の記事 (https://www.fmz.com/digest-topic/4187) では、ペア取引戦略を紹介し、データと数学的分析を使用して取引戦略を作成し、自動化する方法を示しました。

ロングショートバランス株式戦略は、一連の取引対象に適用可能なペア取引戦略の自然な拡張です。これは、デジタル通貨市場や商品先物市場など、さまざまな種類と相互関係を持つ市場の取引に特に適しています。

基本原則

ロングショートバランス株式戦略は、一連の取引対象に対して同時にロングとショートを行うことです。ペア トレーディングと同様に、どの投資対象が安く、どの投資対象が高価かを判断します。違いは、ロング ショート バランス エクイティ戦略では、株式選択プール内のすべての投資対象をランク付けして、どの投資対象が比較的安価か、または高価かを判断することです。次に、ランキングに基づいて上位 n 件の投資をロングし、下位 n 件の投資を同額でショートします (ロング ポジションの合計値 = ショート ポジションの合計値)。

先ほど、ペア取引は市場中立戦略であると述べたことを覚えていますか?ロングショートバランス株式戦略でも同じことが言えます。ロングポジションとショートポジションの額が等しいため、戦略は市場中立（市場変動の影響を受けない）のままになります。この戦略は統計的にも堅牢であり、投資をランク付けして複数のポジションを取ることで、ランク付けモデルを 1 回限りのリスク エクスポージャーではなく、複数のエクスポージャーにさらすことができます。あなたが賭けているのは、ランキング方式の品質だけです。

ランキング制度とは何ですか?

ランキング方式は、予想されるパフォーマンスに基づいて各投資対象に優先順位を割り当てるモデルです。要因としては、価値要因、テクニカル指標、価格設定モデル、またはこれらすべての組み合わせが考えられます。例えば、モメンタム指標を使用してトレンド追随型投資のリストをランク付けすることができます。モメンタムが最も高い投資は引き続き好調なパフォーマンスが期待され、最高のランキングを獲得します。モメンタムが最も低い投資はパフォーマンスが最悪で、最も低い収益率となります。

この戦略の成功は、使用されるランキング スキームにほぼ完全に依存します。つまり、ランキング スキームによって、パフォーマンスの高い投資とパフォーマンスの低い投資を区別し、ロング ショート投資ターゲット戦略のリターンをより適切に実現できるかどうかが重要です。したがって、ランキング方式を開発することが非常に重要です。

ランキングプランを策定するには？

ランキング制度を導入したら、当然、そこから利益を得たいと考えます。私たちは、同じ金額を投資して、上位ランクの投資を買い、下位ランクの投資を空売りすることでこれを実現します。これにより、戦略はランキングの質に比例してのみ収益を得ることになり、「市場中立」になります。

すべての投資を m にランク付けし、投資できる金額が n ドルあり、合計 2p (m>2p) のポジションを保持したいとします。ランク 1 の投資のパフォーマンスが最も悪いと予想される場合、ランク m の投資のパフォーマンスが最も良いと予想されます。

• 投資対象を次のように配置します。1、…、p、ショート2/2p USD投資対象

• 投資対象をm-p、……、mと並べ、n/2pドルの投資対象を買います。

知らせ：価格の急騰による目標価格は必ずしも n/2p を均等に割り切れるわけではなく、一部の目標は整数で購入する必要があるため、不正確なアルゴリズムが存在することになり、アルゴリズムはこの数値に可能な限り近づく必要があります。 n = 100000、p = 500 で戦略を実行すると、次のようになります。

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

これは、端数が 100 を超える価格 (商品先物市場など) では大きな問題を引き起こす可能性があります。端数価格ではポジションを開くことができないためです (この問題は暗号通貨市場には存在しません)。私たちは、端数価格取引を減らしたり、資本を増やしたりすることで、この問題を軽減します。

仮説的な例を見てみましょう。

• Inventor Quantitative Platform 上での研究環境の構築

まず、スムーズに作業を進めるためには、研究環境を構築する必要があります。この記事では、主に便利で高速なAP​​Iを使用できるように、Inventor Quantitative Platform（FMZ.COM）を使用して研究環境を構築します。このプラットフォームのインターフェースとカプセル化は後で行います。完全な Docker システム。

Inventor Quantitative Platform の正式名称では、この Docker システムはホスト システムと呼ばれます。

ホストとロボットの展開方法の詳細については、以前の記事を参照してください: https://www.fmz.com/bbs-topic/4140

独自のクラウド コンピューティング サーバー展開ホストを購入したい読者は、この記事を参照してください: https://www.fmz.com/bbs-topic/2848

クラウドコンピューティングサービスとホストシステムを正常に展開したら、最も強力なPythonツールであるAnacondaをインストールします。

この記事で必要なすべての関連プログラム環境 (依存ライブラリ、バージョン管理など) を実現するには、Anaconda を使用するのが最も簡単な方法です。これは、パッケージ化された Python データ サイエンス エコシステムおよび依存関係マネージャーです。

Anacondaのインストール方法については、Anacondaの公式ガイドを参照してください：https://www.anaconda.com/distribution/

この記事では、Python 科学計算で非常に人気があり重要な 2 つのライブラリである numpy と pandas も使用します。

上記の基本的な作業については、Anaconda環境とnumpyとpandasの2つのライブラリの設定方法を説明した前回の記事も参照してください。詳細については、https://www.fmz.com/digest-をご覧ください。トピック/4169

ランダムな投資とランダムな要因を生成し、ランク付けします。将来の収益が実際にはこれらの要素の値に依存すると仮定しましょう。

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

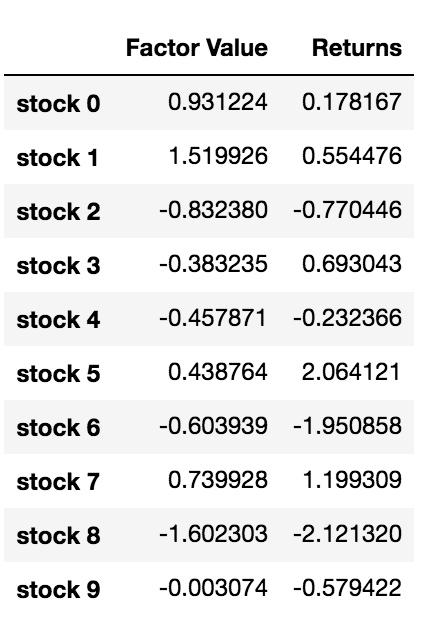
ファクター値とリターンがわかったので、ファクター値に基づいて投資をランク付けし、ロングポジションとショートポジションを開くと何が起こるかを確認できます。

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

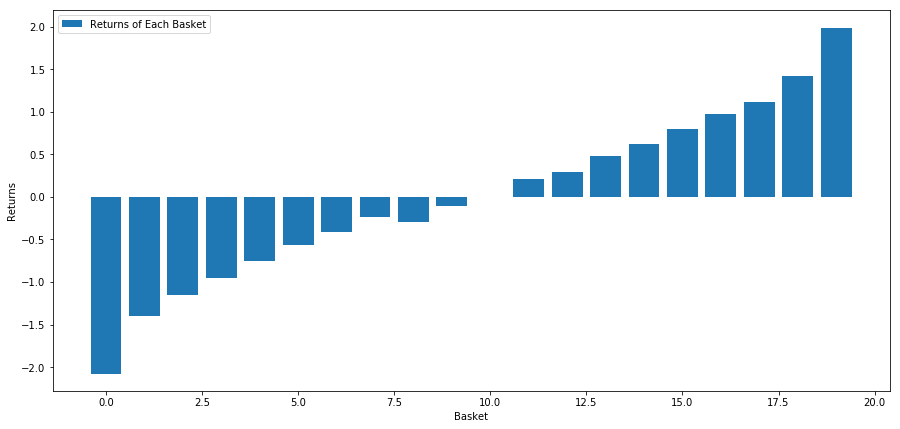
当社の戦略は、投資対象バスケットの中で 1 位にランク付けされた投資をロングし、10 位にランク付けされた投資をショートすることです。この戦略のメリットは次のとおりです。

basket_returns[number_of_baskets-1] - basket_returns[0]

結果は4.172です

当社のランキング モデルに資金を投入して、パフォーマンスの高い投資とパフォーマンスの低い投資を区別します。

この記事の残りの部分では、ランキング スキームを評価する方法について説明します。ランキングベースの裁定取引で利益を上げるメリットは、市場の混乱に左右されず、むしろそれを利用できることです。

実際の例を考えてみましょう。

S&P 500 のさまざまなセクターから 32 銘柄のデータを読み込み、ランク付けしてみます。

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

1か月間の標準化されたモメンタム指標をランキングの基準として使用しましょう

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

ここで、当社の株式の動向を分析し、選択したランキング要因の範囲内で当社の株式が市場でどのように機能するかを確認します。

データを分析する

株価動向

選択した株式バスケットがランキング モデルでどのように機能するかを見てみましょう。これを実行するには、すべての株式の 1 週間先の収益を計算してみましょう。次に、各株式の 1 週間先のリターンと過去 30 日間の勢いの相関関係を確認します。正の相関関係を示す株はトレンド追従型であり、負の相関関係を示す株は平均回帰型です。

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

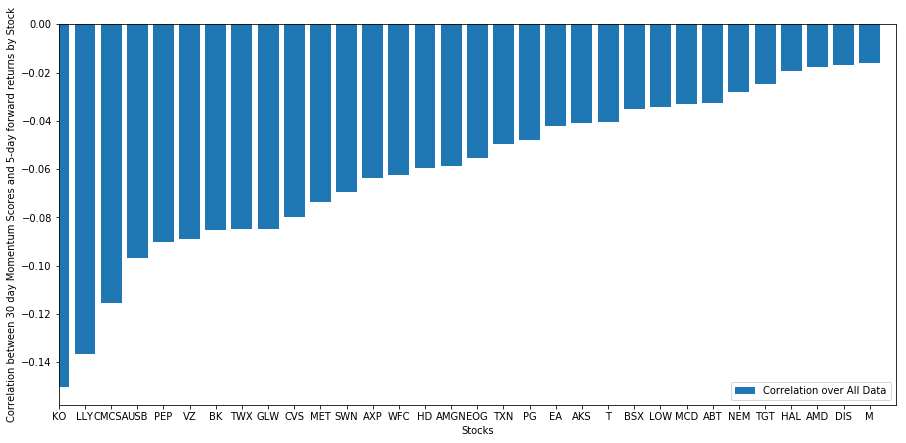
当社のすべての株式は、ある程度平均回帰します。 (どうやら私たちが選んだ世界はこのように機能しているようです) これは、ある株がモメンタム分析で高い順位にランクされている場合、来週はパフォーマンスが低下すると予想すべきであることを示しています。

モメンタムスコアランキングとリターンの相関関係

次に、ランキング スコアと市場全体の将来収益との相関関係、つまり期待収益の予測とランキング要因との関係を確認する必要があります。相関レベルが高いほど相対収益が低くなることが予測されるのでしょうか、あるいはその逆でしょうか。

これを実行するために、すべての株式について、30 日間のモメンタムと 1 週間のフォワード リターンの間の毎日の相関関係を計算します。

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

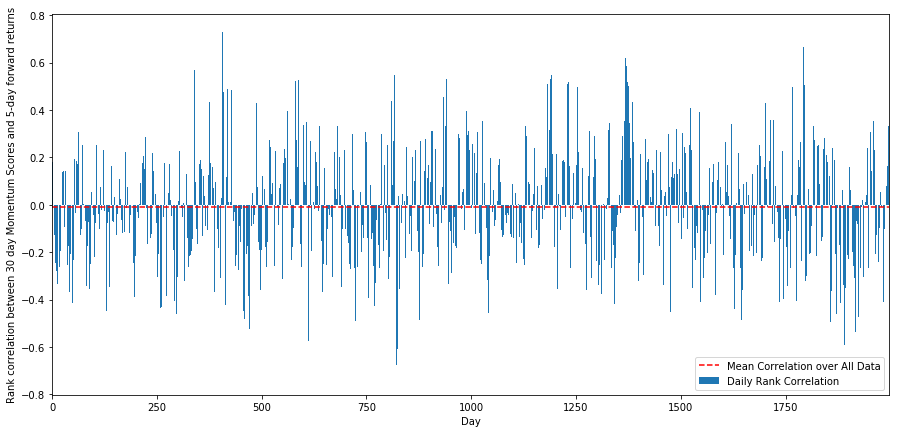
日次相関はかなりノイズが多いですが、非常にわずかです（すべての株式が平均回帰すると言っているので、これは予想通りです）。また、1 か月先のリターンの平均月次相関も見ていきます。

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

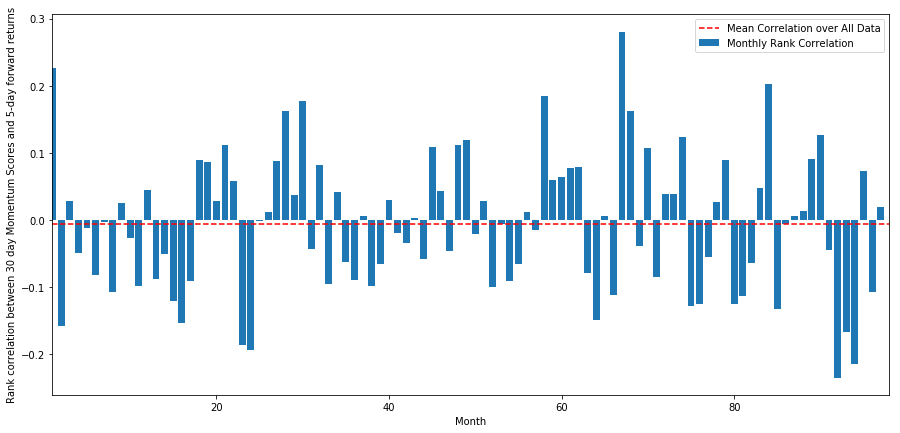
平均相関はここでもわずかに負であることがわかりますが、月ごとに大きく変化します。

平均株式バスケットリターン

当社のランキングから選んだ一連の株式のリターンを計算しました。すべての株式をランク付けし、それを n グループに分けると、各グループの平均収益はいくらになるでしょうか?

最初のステップは、毎月指定された各バスケットの平均リターンとランキング係数を提供する関数を作成することです。

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

このスコアに基づいて株式をランク付けする際に、各バスケットの平均リターンを計算します。これにより、長期にわたる彼らの関係がよくわかるはずです。

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

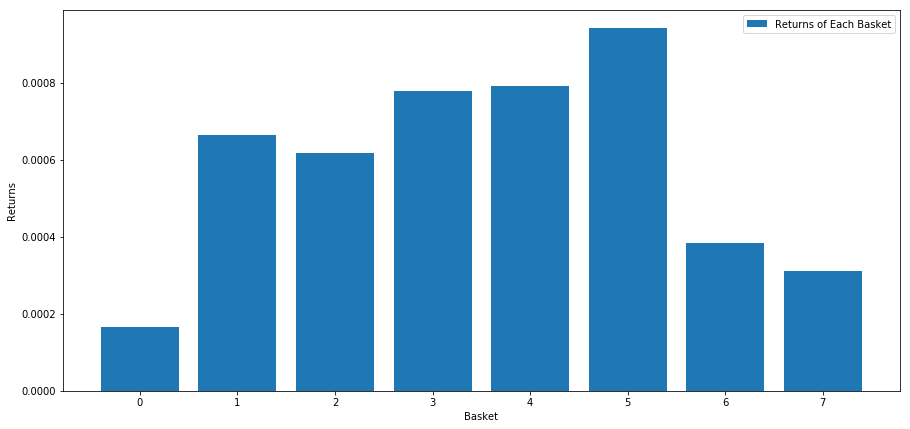
どうやら、パフォーマンスの高い人と低い人を区別できるようになったようです。

スプレッド（基準）の一貫性

もちろん、これらは単なる平均的な関係です。関係がどれだけ一貫しているか、そして取引に応じる意思があるかどうかを理解するためには、時間の経過とともに関係に対するアプローチと姿勢を変える必要があります。次に、過去2年間の月間スプレッド（ベース）を見てみましょう。さらなる変化を確認し、さらに分析を行って、このモメンタム スコアが取引可能かどうかを判断できます。

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

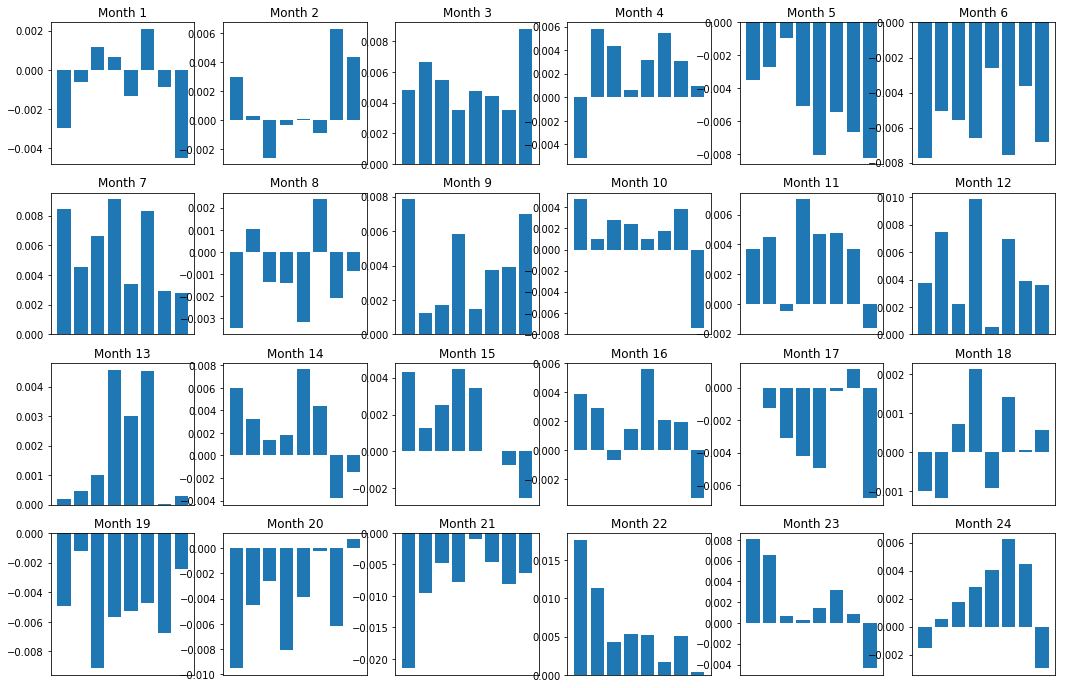
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

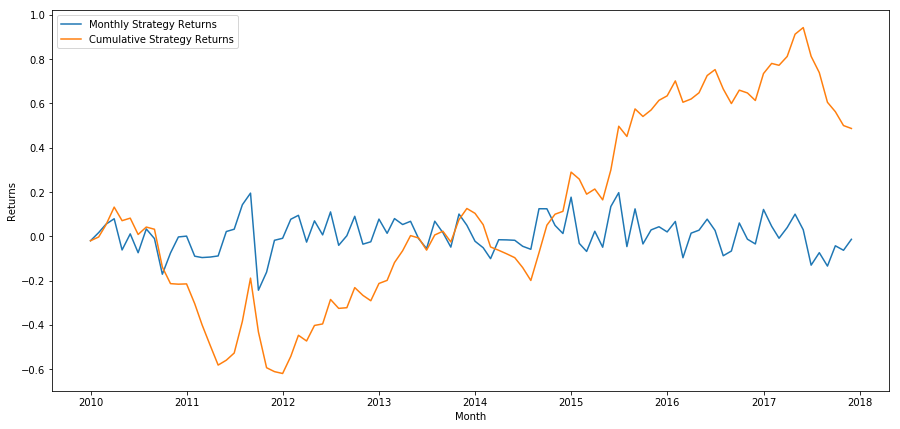
最後に、毎月最後のバスケットをロングし、最初のバスケットをショートした場合のリターンを見てみましょう（各証券に均等に資本を配分すると仮定）

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

年間利回り: 5.03%

私たちのランキング制度は非常に弱く、高パフォーマンスの株式と低パフォーマンスの株式をわずかに区別しているだけであることがわかります。さらに、このランキング方式には一貫性がなく、月ごとに大きく異なります。

適切なランキング方式を見つける

ロングショートバランス株式戦略を実行するには、ランキング方式を決定するだけで十分です。それ以降はすべて機械的です。ロングショートバランス株式戦略を策定したら、他の部分をあまり変更せずに、さまざまなランキング要因を置き換えることができます。これは、毎回コード全体を微調整する必要なく、アイデアをすばやく反復できる非常に便利な方法です。

ランキング スキームは、ほぼすべてのモデルから取得できます。価値ベースのファクターモデルである必要はなく、1か月先のリターンを予測し、それに基づいてランク付けする機械学習技術でもかまいません。

ランキング方式の選択と評価

ランキング方式は、ロングショートバランス株式戦略の利点であり、最も重要な要素でもあります。適切なランキング方式を選択することは体系的なプロジェクトであり、簡単な答えはありません。

良い出発点は、既存の既知のテクノロジーを選択し、それを少し変更してより高い収益を得られるかどうかを確認することです。ここではいくつかの出発点について説明します。

• クローンして調整する: よく議論されているものを選んで、それを少し変更して自分に有利にできるかどうかを確認します。通常、公開要因は市場から完全に裁定取引されているため、取引シグナルを持たなくなります。しかし、時には正しい方向に導いてくれることもあります。

• 価格モデル: 将来の収益を予測するモデルはいずれも要因となる可能性があり、取引対象のバスケットをランク付けするために使用できる可能性があります。複雑な価格設定モデルをランキング方式に変換できます。

• 価格ベースの要因（テクニカル指標）今日説明したような価格ベースのファクターは、各株式の過去の価格に関する情報を取得し、それを使用してファクター値を生成します。例としては、移動平均指標、モメンタム指標、ボラティリティ指標などが挙げられます。

• 回帰と勢い: 価格が一度一方向に動くと、その動きが続くと考える要因があることは注目に値します。いくつかの要因はまったく逆です。どちらも異なる時間枠と資産に対して有効なモデルであり、基礎となる動作がモメンタムベースか回帰ベースかを調べることが重要です。

• 基本的な要因（価値ベース）: これは、PE、配当金などの基本的な価値の組み合わせを使用しています。ファンダメンタル価値には、企業に関する現実世界の事実に関連した情報が含まれているため、多くの点で価格よりも強力になる可能性があります。

結局のところ、予測子の開発は、常に一歩先を行くための軍拡競争なのです。ファクターは市場から裁定取引され、寿命があるため、ファクターがどの程度劣化したか、また、それを置き換えるためにどのような新しいファクターを使用できるのかを判断する作業を継続的に行う必要があります。

その他の考慮事項

• リバランス頻度

各ランキング システムは、わずかに異なる期間にわたってリターンを予測します。価格ベースの平均回帰は数日間にわたる予測が可能かもしれませんが、価値ベースのファクターモデルは数か月にわたる予測が可能かもしれません。戦略を実行する前に、モデルが予測する時間範囲を決定し、それを統計的に検証することが非常に重要です。リバランスの頻度を最適化しようとして過剰適合することは避けてください。必然的に、他のものよりランダムに優れたものを見つけてしまいます。ランキング方式で予測される期間を決定したら、その頻度でリバランスを試みてください。モデルを最大限に活用しましょう。

• 資本能力と取引コスト

各戦略には最小および最大の資本要件があり、最小しきい値は通常、取引コストによって決まります。

あまり多くの株式を取引すると、取引コストが高くなります。 1,000 株を購入したい場合、リバランスごとに数千ドルのコストが発生します。資本基盤は、取引コストが戦略によって生み出される収益のごく一部を占める程度に十分に高くなければなりません。たとえば、資本が 100,000 ドルで、戦略によって毎月 1% (1,000 ドル) の収益が得られる場合、その収益はすべて取引コストによって消えてしまいます。この戦略を実行して 1,000 株以上で利益を上げるには、数百万ドルの資本が必要になります。

最小資産額は主に取引される株式数によって決まります。しかし、最大容量も非常に高く、ロングショートバランス株式戦略では、優位性を失うことなく数億ドルの取引が可能です。これは、この戦略が比較的まれにしか再調整されないためです。総資産額を取引された株式数で割ると、1 株あたりのドル価値は非常に低くなり、取引量によって市場が動くことを心配する必要はありません。 1,000 株を取引すると、1 億ドルになります。毎月ポートフォリオ全体のバランスを調整した場合、1 株あたり 1 か月あたり 10 万ドルしか取引されないため、ほとんどの証券で大きな市場シェアを獲得するには不十分です。