당신이 마스터해야 할 7가지 회귀 기술

**이 글은 회귀 분석과 그 장점을 설명하고, 선형 회귀, 논리 회귀, 다항적 회귀, 단계적 회귀, ?? 회귀, 꼬리 회귀, ElasticNet 회귀 등 가장 많이 사용되는 7가지 회귀 기술과 그 핵심 요소를 요약하고, 마지막으로 올바른 회귀 모델을 선택하는 핵심 요소를 소개한다. ** ** 编辑자 버튼 회귀 분석은 모델링 및 데이터를 분석하는 중요한 도구이다. 이 글은 회귀 분석의 의미와 장점을 설명하고, 선형 회귀, 논리 회귀, 다항식 회귀, 단계적 회귀, 회귀, 꼬리줄 회귀, ElasticNet 회귀 등 가장 많이 사용되는 7가지 회귀 기술과 그 핵심 요소를 요약하고, 마지막으로 올바른 회귀 모델을 선택하는 핵심 요소를 소개한다.**

• ### 회귀 분석이란 무엇인가요?

회귀 분석 (回帰分析, 영어: regression analysis) 은 인수변수 (因變數, target) 와 자기변수 (自變數, predictor) 사이의 관계를 연구하는 예측적 모델링 기술이다. 이 기술은 일반적으로 예측 분석, 시간계열 모델, 그리고 발견된 변수 사이의 인과관계를 위해 사용된다. 예를 들어, 운전자의 무분별한 운전과 도로 교통 사고의 수 사이의 관계를 연구하는 가장 좋은 방법은 회귀이다.

회귀 분석은 데이터를 모델링하고 분석하는 데 중요한 도구입니다. 여기 우리는 곡선/라인으로 이 데이터 포인트를 맞추고, 이 방법으로 곡선이나 선에서 데이터 포인트까지의 거리의 차이는 최소화됩니다.

• ### 왜 우리는 회귀 분석을 사용합니까?

앞서 언급한 바와 같이, 회귀 분석은 두 개 이상의 변수 사이의 관계를 추정한다. 아래에서, 그것을 이해하기 위해 간단한 예를 들어 보겠습니다:

예를 들어, 현재 경제 조건에서, 당신은 회사의 매출 성장률을 추정해야 합니다. 이제, 당신은 회사의 최신 데이터를 가지고 있습니다. 이 데이터는 매출 성장률이 경제 성장률의 약 2.5배를 나타냅니다. 그래서 회귀 분석을 사용하여, 우리는 현재와 과거의 정보를 기반으로 미래의 회사의 매출을 예측할 수 있습니다.

회귀 분석을 사용하는 데는 많은 이점이 있다. 구체적으로 다음과 같다:

그것은 자기 변수와 인과 변수의 뚜렷한 관계를 나타냅니다.

이는 여러 자기 변수가 하나의 인과 변수에 미치는 영향의 강도를 나타낸다.

회귀 분석은 또한 가격 변화와 프로모션 활동의 수와 같은 다른 척도를 측정하는 변수 간의 상호 영향을 비교 할 수 있습니다. 이것은 시장 연구원, 데이터 분석가 및 데이터 과학자가 예측 모델을 구축하기 위해 최적의 변수를 제거하고 추정하는 데 도움이됩니다.

• ### 우리는 몇 가지 복귀 기술을 가지고 있습니까?

다양한 회귀 기술이 예측에 사용된다. 이 기술들은 주로 세 가지의 측량 (自變數의 개수,因變數의 종류, 그리고 회귀선의 모양) 을 가지고 있다. 우리는 다음 부분에서 그것들을 자세히 논의할 것이다.

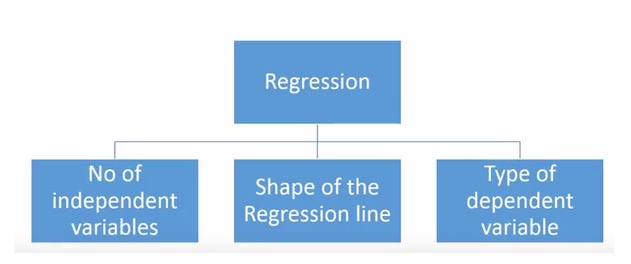
창의적인 사람들을 위해, 위의 변수들의 조합을 사용하는 것이 필요하다고 생각하면, 사용되지 않은 회귀 모델을 만들 수도 있습니다. 하지만 시작하기 전에, 가장 일반적으로 사용되는 회귀 방법을 알아보십시오.

• 1. Linear Regression 선형 회귀

  가장 잘 알려진 모델링 기술 중 하나이다. 선형 회귀는 일반적으로 예측 모델을 학습할 때 선호하는 기술 중 하나이다. 이 기술에서 변수가 연속적이므로 자기 변수가 연속적이거나 분산적이거나 회귀선의 성질은 선형적이다.

  선형 회귀는 최적의 합쳐진 직선 ((즉, 회귀선) 을 사용하여 인수변수 ((Y) 와 하나 이상의 자기변수 ((X) 사이에 관계를 구축한다.

  y=a+b라는 식을 써봅시다*X + e, 여기서 a는 절단, b는 직선의 기울기, e는 오차항이다. 이 방정식은 주어진 예측 변수 (s) 에 따라 목표 변수의 값을 예측할 수 있다.

  

  일선형 회귀와 다중선형 회귀의 차이점은, 다중선형 회귀에는 [[>1]]개의 자변이 있고, 일선형 회귀는 보통 1개의 자변이 있다. 이제 문제는 어떻게 하면 최적의 합치선을 얻을 수 있는가? 。

  어떻게 a와 b의 값을 얻을 수 있을까요?

  이 문제는 최소 2 곱셈을 사용하여 쉽게 수행할 수 있다. 최소 2 곱셈은 회귀선을 합치기 위한 가장 일반적인 방법이다. 관측 데이터의 경우, 각 데이터 포인트의 수직 편차의 제곱을 줄이면서 최적 합치선을 계산한다. 합치면 편차가 먼저 제곱되기 때문에, 양과 음값은 상쇄되지 않는다.

  

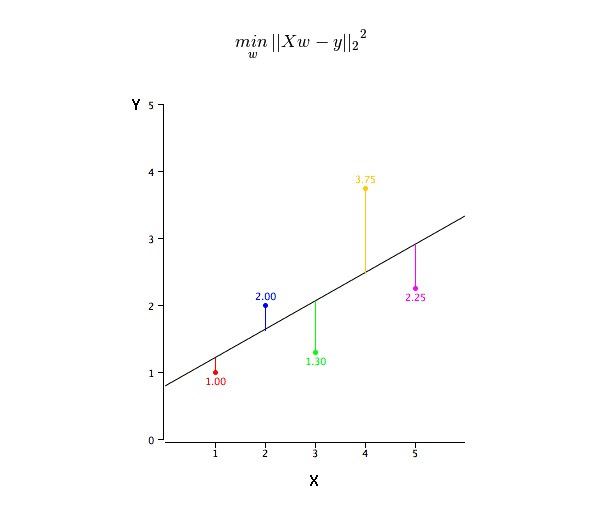
  우리는 R-square 지표를 사용하여 모델 성능을 평가할 수 있다. 이 지표에 대한 자세한 내용은: 모델 성능 지표 Part 1, Part 2를 참조하십시오.

  요점:

  • 자기 변수와 인수 변수 사이에 선형적인 관계가 있어야 한다
  • 다중 회귀에는 다중 동선성, 자기관계성 및 이차차성이 있다.
  • 선형 회귀는 이례값에 매우 민감하다. 이는 회귀선에 심각한 영향을 미치고, 결국 예측값에 영향을 미칩니다.
  • 다중공선성은 계수 추정값의 차원을 증가시키며, 모델의 작은 변화로 인해 매우 민감하게 추정된다. 결과적으로 계수 추정값은 불안정하다.
  • 여러 개의 자변의 경우, 우리는 최우선 자변을 선택하기 위해 앞선 선택법, 뒷선 제거법, 그리고 점진적인 필터링법을 사용할 수 있다.

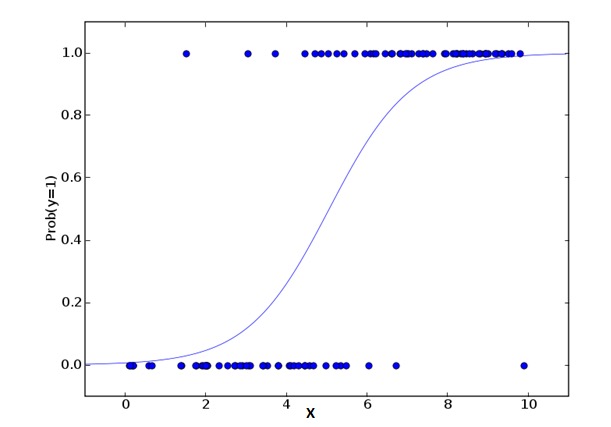
• 2. Logistic Regression 논리적 회귀

  논리 회귀는 이벤트=Success 및 이벤트=Failure의 확률을 계산하기 위한 것이다. 왜냐하면 변수의 유형이 이진적인 변수 ((¹⁄₀, true/false, yes/no) 에 속할 때, 우리는 논리 회귀를 사용해야 한다. 여기서, Y의 값은 0에서 1까지이며, 다음과 같은 방정식으로 나타낼 수 있다.

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  위의 공식에서, p가 어떤 특성을 갖는 확률을 나타냅니다. 여러분은 이런 질문을 해야 합니다. 왜 우리는 공식에서 논수 로그를 사용합니까?

  여기서 우리가 사용하는 것이 이차 분포 ((변수)) 이기 때문에, 우리는 이 분포에 대해 최적의 결합 함수를 선택해야 한다. 그것은 Logit 함수이다. 위의 방정식에서, 샘플의 극대 가망 추정값을 관찰하여 파라미터를 선택한다, 대신 제곱과 오류를 최소화하지 않는다. (일반 회귀에서 사용되는 것처럼).

  

  요점:

  • 분류문제에 널리 사용된다.
  • 논리 회귀는 자기 변수와 인수 변수가 선형적인 관계를 필요로 하지 않는다. 그것은 예측된 상대적 위험 지수 OR에 비선형적인 로그 변환을 사용하기 때문에 다양한 유형의 관계를 처리할 수 있다.
  • 지나치게 잘 어울리는 것과 잘 어울리지 않는 것을 피하기 위해, 우리는 모든 중요한 변수를 포함해야 한다. 이러한 상황을 보장하기 위한 좋은 방법은, 점진적 필터링 방법을 사용하여 논리 회귀를 추정하는 것이다.
  • 그것은 큰 샘플 수를 필요로 하기 때문에, 샘플 수를 적게 하는 경우, 극히 가능성이 있는 추정 효과는 일반적인 최소 2 곱하기보다 나쁘다.
  • 자기 변수는 상호 연관되어서는 안 되며, 즉 다중 공선성이 없다. 그러나, 분석과 모델링에서, 우리는 분류 변수의 상호 작용을 포함하는 것을 선택할 수 있다.
  • 만약 인수 변수의 값이 순서 변수라면, 그것을 순서 논리 회귀라고 한다.
  • 만약 인수 변수가 다중 종류라면, 다중 논리 회귀라고 한다.

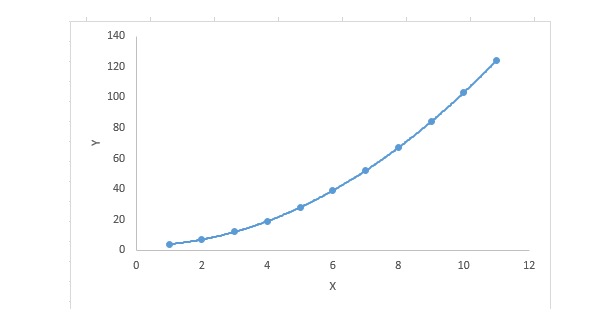
• 3. Polynomial Regression 다항식 회귀

  회귀 방정식에는 자기 변수의 지수가 1보다 크면 다항 회귀 방정식이다. 다음과 같은 방정식이 있다:

  y=a+b*x^2
  

  이러한 회귀 기술에서, 최적의 합치는 직선이 아니라, 데이터 포인트를 합치는 곡선이다.

  

  주요 내용:

  • 고차원 다항식을 합쳐서 더 낮은 오류를 얻을 수 있는 유도이 있을지라도, 이것은 과합을 초래할 수 있다. 당신은 종종 관계 도표를 그려서 적합성을 확인하고, 과합도 결합도 없는 합리적인 적합성을 보장하는 데 집중해야 한다. 아래는 이해를 돕기 위한 도표이다:

  

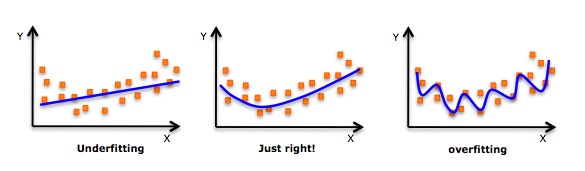
  • 분명히 양쪽 끝으로 곡선의 점들을 찾아보고 이러한 모양과 경향들이 의미가 있는지 살펴보세요. 더 높은 계열의 다항식은 결국 기묘한 추론 결과를 낳을 수 있습니다.

• 4. 단계적 회귀

  여러 개의 자변을 처리할 때, 우리는 이러한 형태의 회귀를 사용할 수 있다. 이 기술에서, 자변의 선택은 비인도적인 조작을 포함한 자동화된 과정에 의해 이루어진다.

  이 과제는 R-square, t-stats 및 AIC 지표와 같은 통계적 값을 관찰하여 중요한 변수를 식별하는 것입니다. 점진적 회귀는 지정된 기준에 기반한 동변을 동시에 추가 / 삭제하여 모델을 적합하게합니다. 가장 일반적으로 사용되는 점진적 회귀 방법은 다음과 같습니다.

  • 표준 점진적 회귀법은 두 가지 일을 한다. 즉, 각 단계에 필요한 예측을 더하고 제거한다.
  • 전향 선택은 모델에서 가장 눈에 띄는 예측부터 시작하여, 각 단계에 대해 변수를 추가한다.
  • 후진 제거법은 모델의 모든 예측과 동시에 시작되고, 그 다음 각 단계마다 최소의 중요한 변수를 제거한다.
  • 이 모델링 기술은 최소한의 예측 변수를 사용하여 예측 능력을 극대화하기 위한 것입니다. 이것은 또한 고차원 데이터 세트를 처리하는 방법 중 하나입니다.

• 5. 리지 회귀

  회귀 분석 ( regression analysis) 은 다중공선성 (多重共線性, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity, 영어: multiple co-linearity) 이 있다.

  위의 것은 선형 회귀 방정식입니다. 기억하세요?

  y=a+ b*x
  

  이 방정식에도 오류항이 있다. 완전한 방정식은 다음과 같다:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  선형적 방정식에서, 예측 오류는 2개의 분수로 나눌 수 있다. 하나는 편차이고, 하나는 차차이다. 예측 오류는 이 두 가지 분량 또는 이 두 가지 중 어느 하나에 의해 발생할 수 있다. 여기서 우리는 차차로 인해 발생하는 관련 오류를 논의할 것이다.

  회귀는 축약 변수 λ[lambda]를 사용하여 다중공선성 문제를 해결한다. 아래의 공식을 참조하십시오.

  

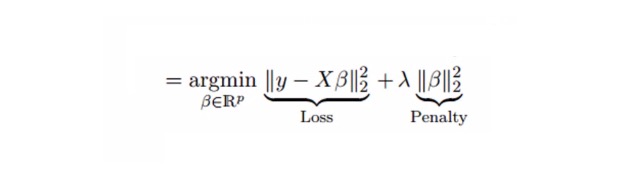
  이 공식에는 두 가지 구성 요소가 있다. 하나는 최소 2배제이고, 다른 하나는 β2 (β-제곱) 의 λ배제이며, 여기서 β는 관련 계수이다. 수축 변수를 최소 2배제 안에 추가하여 매우 낮은 차원을 얻는다.

  요점:

  • 상수를 제외한 이 회귀의 가정은 최소 2배 회귀와 비슷하다.
  • 그것은 관련 계수의 값을 축소하지만 0에 도달하지 않습니다. 이것은 특징 선택 기능이 없다는 것을 나타냅니다.
  • 이것은 정규화 방법이며, L2 정규화를 사용합니다.

• 6. 라소 회귀

  회귀와 비슷하며, Lasso (Least Absolute Shrinkage and Selection Operator) 도 회귀 계수의 절대값 크기를 처벌한다. 또한, 그것은 변화의 정도를 줄이고 선형 회귀 모델의 정확도를 향상시킬 수 있다. 아래의 공식을 참조하십시오:

  

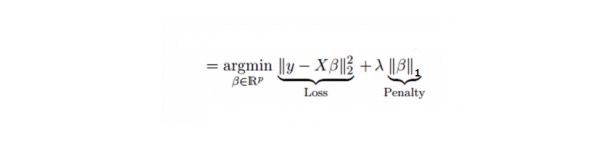
  라소 회귀는 리지 회귀와 약간 다르며, 징벌 함수는 사각형이 아닌 절대값을 사용한다. 이것은 징벌 (또는 억제된 추정치의 절대값의 합) 값이 몇 가지 변수 추정 결과를 0으로 만들게 한다. 징벌 값을 더 많이 사용하면 더 많은 추정은 축소 값을 0에 가깝게 만들 것이다. 이것은 우리가 주어진 n 변수 중에서 변수를 선택하도록 만들 것이다.

  요점:

  • 상수를 제외한 이 회귀의 가정은 최소 2배 회귀와 비슷하다.
  • 수축 계수는 0에 가깝고, 이는 특징 선택에 도움이 됩니다.
  • 이것은 L1 정규화를 사용하는 정규화 방법입니다.
  • 만약 예측된 변수들의 집합이 매우 연관되어 있다면, 라소 (Lasso) 는 그 중 하나의 변수를 선택하고 다른 변수를 0으로 축소한다.

• 7. ElasticNet의 회귀

  ElasticNet은 라소와 리지 회귀 기술의 혼합물이다. L1을 사용하여 훈련하고 L2를 정규화 매트릭스로 우선한다. 여러 개의 관련 특성이 있을 때 ElasticNet은 유용하다. 라소는 그들 중 하나를 무작위로 선택하고, ElasticNet은 둘을 선택한다.

  

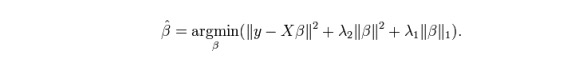
  Lasso와 Ridge의 실질적인 장점은, ElasticNet이 Ridge의 안정성을 순환 상태에서 물려받을 수 있다는 것이다.

  요점:

  • 그리고 그것은 고도로 연관된 변수의 경우 집단효과를 가져옵니다.
  • 선택 가능한 변수의 수는 제한되지 않습니다.
  • 두 번 수축할 수 있습니다.
  • 이 7가지의 가장 많이 사용되는 회귀 기술 외에도, 베이지안 회귀, 에콜로기컬 회귀, 로버스트 회귀와 같은 다른 모델들을 살펴볼 수 있습니다.

• 어떻게 regression 모델을 선택해야 할까요?

  한 두 가지 기술만 알고 있을 때 인생은 보통 간단하다. 제가 아는 한 교육 기관은 학생들에게, 결과가 연속적이라면, 선형 회귀를 사용하라, 그리고 이진적이라면, 논리 회귀를 사용하라, 라고 말했습니다. 하지만, 우리의 처리에 있어서, 선택할 수 있는 것이 많을수록, 올바른 것을 선택하는 것이 더 어려워집니다. 회귀 모델에서도 비슷한 상황이 일어납니다.

  다중 회귀 모델에서, 자기 변수와 인수 변수의 유형, 데이터의 차원, 그리고 데이터의 다른 기본 특성에 따라 가장 적합한 기술을 선택하는 것은 매우 중요합니다. 다음이 올바른 회귀 모델을 선택하는 중요한 요소입니다:

  데이터 탐구는 예측 모델을 구축하는 필수적인 부분이다. 적절한 모델을 선택할 때, 예를 들어 변수의 관계와 영향을 식별할 때, 우선적으로 선택되어야 한다.

  서로 다른 모델의 장점을 비교할 때, 우리는 다른 지표 파라미터를 분석할 수 있습니다. 예를 들어, 통계적 의미의 파라미터, R-square, Adjusted R-square, AIC, BIC, 그리고 오류 항목, 다른 하나는 Mallows’ Cp 가이드라인입니다. 이것은 주로 모델을 가능한 모든 하위 모델과 비교하거나, 신중하게 선택하여, 당신의 모델에서 발생할 수있는 편차를 검사합니다.

  크로스 검증은 예측 모델을 평가하는 가장 좋은 방법이다. 여기서, 여러분의 데이터 세트를 두 부분으로 나누세요. 하나의 훈련과 하나의 검증으로. 관찰값과 예측값 사이의 간단한 평형 차이를 사용하여 여러분의 예측 정확도를 측정하세요.

  만약 여러분의 데이터 세트가 여러 개의 혼합 변수라면, 여러분은 자동 모델 선택 방법을 선택해서는 안 됩니다. 왜냐하면 여러분은 모든 변수를 동시에 동일한 모델에 넣고 싶지 않으니까요.

  그것은 또한 당신의 목적에 따라 달라질 것입니다. 이런 상황이 발생할 수 있습니다. 덜 강력한 모델은 높은 통계학적 의미의 모델보다 더 쉽게 구현됩니다.

  회귀 정규화 방법 ((Lasso, Ridge, and ElasticNet) 은 고차원 및 데이터셋 변수들 사이의 다중 공선성 상황에서 잘 작동한다.

[사진: CSDN]