선형 회귀 - 최소 제곱법

• ### 1 개막

이 기간 동안 기계 학습 , 제5장 Logistic 회귀 , 배움은 상당히 힘들어졌다. 본 자료를 거슬러 올라가면, Logistic 회귀 에서 선형 회귀 으로, 그 다음으로 최소 제곱법 으로. 최종적으로 고등 수학 ((제6판; 하부판) 제9장 제10항 최소 제곱법 에 이르게 된다. 이것은 최소 제곱법의 뒷부분의 수학 원리가 어디에서 왔는지 이해한다. 최저 2 곱하기 은 최적화 문제에서 경험 공식을 구축하는 방법 중 하나이다. 그것의 원리를 이해하는 것은 Logistic 회귀 과 지원 벡터 기계의 학습 에 대해 이해하는 데 유용하다.

• ### 2 배경 지식

最小二乘法이 등장한 역사적 배경은 매우 흥미롭습니다.

1801년, 이탈리아의 천문학자 조세프 피아치는 최초의 소행성 골짜기 별을 발견했다. 40일간의 추적 관측 후, 골짜기 별이 태양 뒤쪽으로 이동하면서 피아치가 골짜기의 위치를 잃었다. 이후 전 세계의 과학자들은 피아치의 관측 데이터를 사용하여 골짜기 별을 찾기 시작했다. 그러나 대부분의 사람들의 계산에 따라 골짜기 별을 찾는 결과는 없었다. 당시 24세였던 고스도 골짜기 별의 궤도를 계산했다. 오스트리아의 천문학자 인히리히 올버스는 고스의 계산에 따라 골짜기 별의 궤도를 재발견했다.

고스가 사용한 최소 2배제법의 방법은 1809년에 그의 저서 ?? 천체 운동론 ?? 에서 발표되었으며, 프랑스의 과학자 레잔드는 1806년에 독립적으로 최소 2배제법의 원리를 발견했지만, 당시에는 알려지지 않았기 때문에 묵묵히 알려지지 않았다. 두 사람은 최소 2배제법의 원리를 누가 가장 먼저 만들었다는 논란이 있었다.

1829년, 고스는 최소 2배법의 최적화 효과가 다른 방법보다 더 강력하다는 것을 증명하였다. 고스-마르코프 정리 (Gauss-Markov theorem) 를 참조하십시오.

• ### 3. 지식의 활용

最小二乘法의 핵심은 모든 데이터의 편차의 제곱과最小을 보장하는 것이다.

만약 우리가 몇 개의 선박의 길이와 너비 데이터를 수집한다면

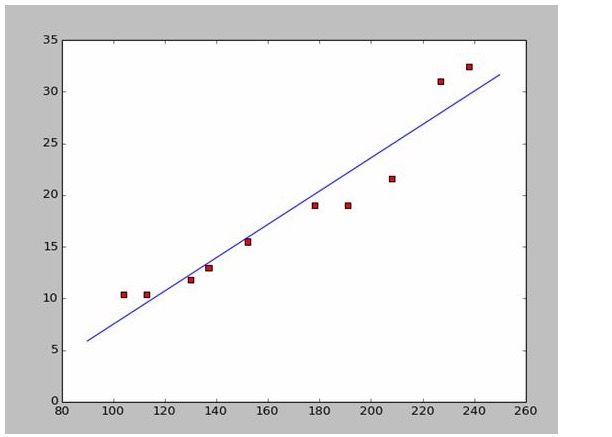
이 자료를 토대로, 우리는 파이썬으로 분산점 지도를 그리는데 사용했습니다.

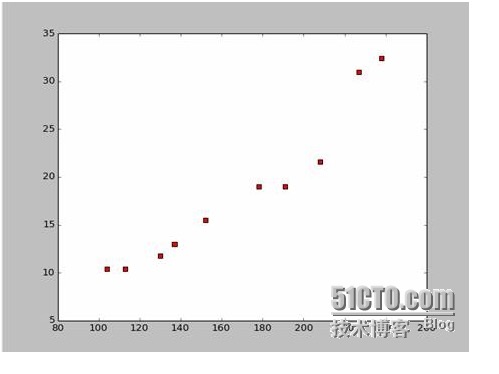
이 지도는 다음과 같습니다.

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

238,32.4) 와 152,15.5) 를 빼면 두 개의 방정식이 나옵니다 152*a+b=15.5 328*a+b=32.4 a=0.197이고, b=-14.48이 됩니다. 그리고 우리는 이런 모형의 그래프를 얻을 수 있습니다.

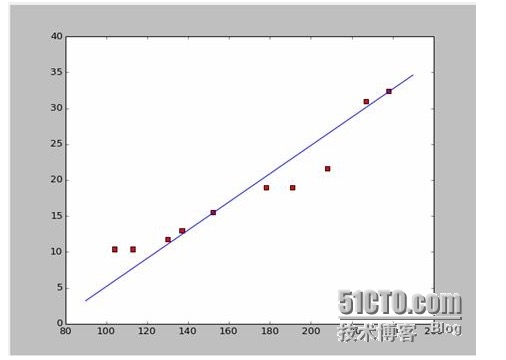
자, 이제 새로운 질문이 생겼습니다. a와 b가 최적화 가능한가요? 전문적으로 말하자면, a와 b가 모델의 최적화 가능한 매개 변수인가요?

답은: 모든 데이터의 차이의 제곱과 최소를 보장한다. 원칙에 관해서는, 우리는 나중에 이 도구를 사용하여 어떻게 a와 b를 가장 잘 계산할 수 있는지 살펴볼 것이다. 모든 데이터의 제곱과 최소를 M로 가정하면,

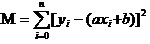
이제 우리가 해야 할 일은 M의 최소 a와 b를 구하는 것입니다.

이 방정식은 a, b를 자기 변수로 하고 M를 인수 변수로 하는 이진 함수입니다.

고수에서 1차 함수가 어떻게 극한값이 되는지 생각해 봅시다. 우리는 이산 함수에서 이산 함수를 사용한다. 이산 함수에서는 여전히 이산 함수를 사용한다. 이산 함수에는 새로운 이름이 붙여져 있다. 이산 함수는 두 변수 중 하나를 상수로 간주하여 이산 함수를 구하는 것이다. M에 대한 편도함수를 구하면

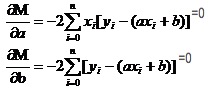
이 두 방정식에서 x와 y는 모두 알려져 있다.

이 문서는 위키피디아 자료를 이용한 것으로, 저는 여기서 직접 답변을 사용하여 일치하는 이미지를 그려보겠습니다:

  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### 네, 탐구

데이터 매칭에서, 왜 모델의 예측 데이터와 실제 데이터의 차이의 제곱을 절대값과 최소값 대신 모델 매개 변수를 최적화하도록 하는가?

이 질문에 이미 답변이 되어 있습니다. 링크를 참조하십시오.

개인적으로는 이 설명이 매우 흥미롭다고 생각합니다. 특히 그 안의 가정: f (x) 에서 벗어난 모든 지점은 소음이 있습니다.

한 점이 멀어질수록 잡음이 커질수록, 이 점의 발생 확률도 낮아진다. 그렇다면, 한 점이 멀어질 정도 x가 발생 확률 f (x) 와 어떤 관계를 갖는가? 정형 분포이다.

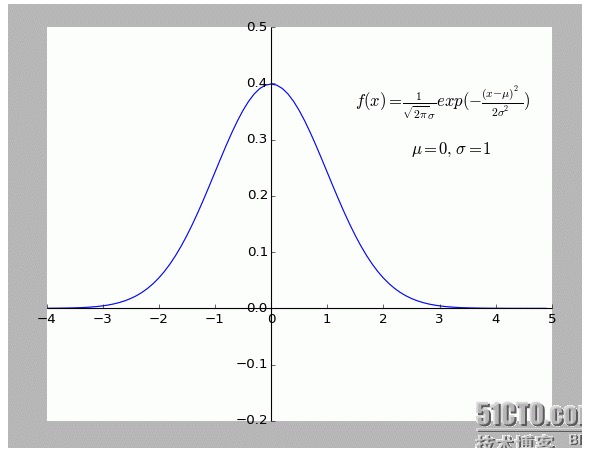
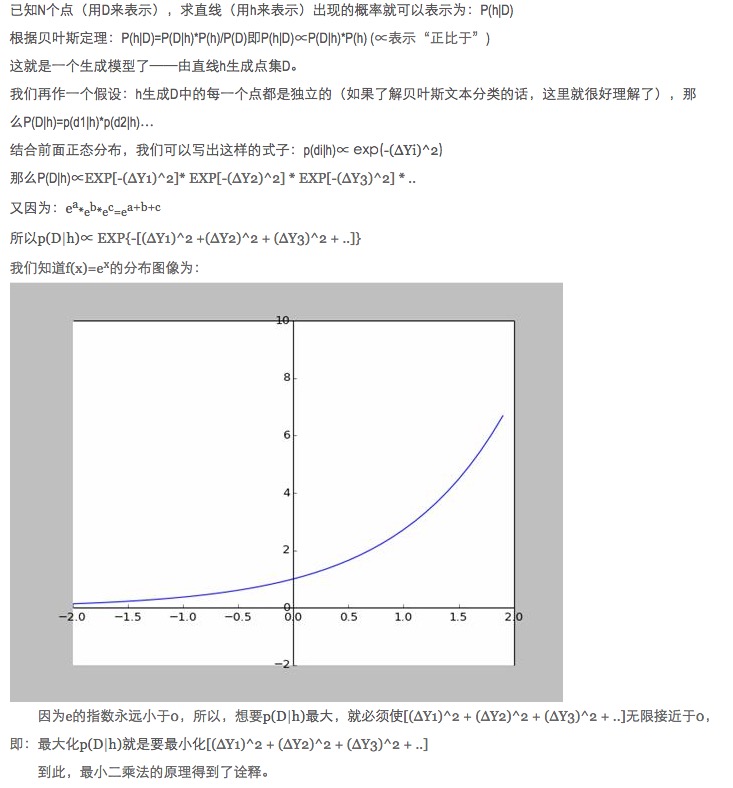
• ### 다섯째, 확장

위의 것은 2차원적인 상황, 즉 하나의 자기 변수뿐이다. 그러나 현실 세계에서 최종 결과에 영향을 미치는 것은 여러 가지 요인의 중첩이다. 즉 자기 변수가 여러 가지의 상황이 있을 것이다.

일반 N개의 미터선형 함수들에 대해, 선형대수열의 역행렬로 해답을 구하는 것은 괜찮습니다; 일시적으로 적절한 예가 발견되지 않았기 때문에, 하나의 인자로 여기 남겨두겠습니다.

물론 자연은 단순한 선형성이 아닌 다항적 적합성이 더 많고, 그것은 더 높은 수준입니다.

• 참고문헌

  • 고등 수학 (제6판) (高等教育出版社)
  • 선형대수 (北京大学出版社)
  • 인터랙티브 백과사전:최소 2 곱하기
  • 위키피디아: 최소 2 곱셈
  • 과학 네트워크:최소 2 곱하기? 신마에게 나쁜 절대값은 아닙니다.

원본 저작물, 재배송이 허용되는 경우, 재배송할 때 반드시 하이퍼링크 형식으로 기사의 원본과 저자 정보 및 본 선언을 표시하십시오. 그렇지 않으면 법적 책임을 져야합니다. http://sbp810050504.blog.51cto.com/2799422/1269572