Regresi linear - kaedah kuasa dua terkecil

• ### 1. Perkenalan

Pada masa ini, saya belajar untuk mengurutkan mesin untuk mengurutkan, dan saya belajar untuk mengurutkan pengulangan logistik dalam bab 5. Saya merasa agak sukar. Saya mengurutkan semula, dari pengulangan logistik ke pengulangan linear, dan kemudian ke pengulangan penggandaan minimum. minimum dua kali ganda adalah satu cara untuk mewujudkan formula pengalaman dalam masalah pengoptimuman. Memahami prinsipnya berguna untuk memahami Logistic regression dan support vector machine learning .

• ### B. Keterangan latar belakang

Latar belakang sejarah munculnya pecahan dua kali ganda terkecil adalah menarik.

Pada tahun 1801, ahli astronomi Itali Giuseppe Piazzi menemui asteroid pertama, Ceres. Selepas 40 hari pemerhatian, Piazzi kehilangan lokasi Ceres kerana ia berada di belakang Matahari. Kemudian, saintis di seluruh dunia menggunakan data pemerhatian Piazzi untuk mencari Ceres, tetapi tidak ada hasil berdasarkan perhitungan kebanyakan orang. Gauss, yang berusia 24 tahun, juga mengira orbit Ceres.

Kaus menggunakan kaedah penggandaan dua yang paling kecil yang diterbitkan dalam bukunya pada tahun 1809 Theory of the Movement of Celestial Bodies, dan saintis Perancis Lejeune secara berasingan menemui penggandaan dua yang paling kecil pada tahun 1806, tetapi tidak diketahui kerana tidak diketahui pada masa itu. Kedua-dua orang itu pernah berselisih mengenai siapa yang pertama kali membuat prinsip penggandaan dua yang paling kecil.

Pada tahun 1829, Gauss memberikan bukti bahawa kesan pengoptimuman untuk penggandaan dua terkecil lebih kuat daripada kaedah lain, lihat Teorema Gauss-Markov.

• ### Ketiga, penggunaan pengetahuan

Titik inti dari persamaan dua kali ganda terkecil adalah untuk menjamin semua data yang menyimpang dari segi kuasa dua dan terkecil.

Katakanlah kita mengumpul data panjang dan lebar kapal perang.

Dari data ini, kami telah menggunakan Python untuk melukis peta titik-titik:

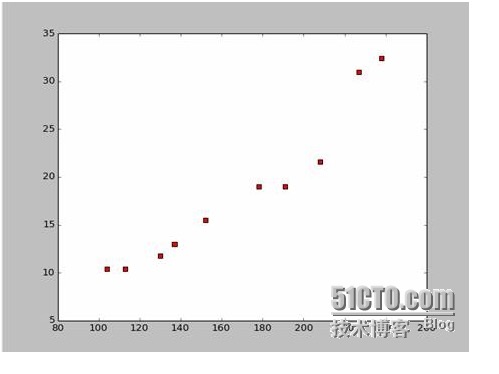
Ini adalah kod untuk peta titik-titik:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Jika kita ambil kedua-dua titik pertama, 238, 32.4, 152, 15.5, kita akan dapat kedua-dua persamaan. 152*a+b=15.5 328*a+b=32.4 Jadi, kita dapat a = 0.197 dan b = -14.48. Jadi, kita boleh mendapatkan persamaan seperti ini:

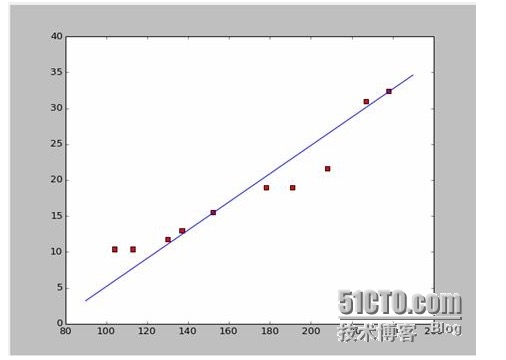
Baiklah, soalan baru muncul, adakah a dan b adalah penyelesaian optimum? dalam bahasa profesional, adakah a dan b adalah parameter optimum model? sebelum menjawab soalan ini, mari kita selesaikan soalan lain: apakah syarat yang akan dipenuhi oleh a dan b?

Jawapannya ialah: menjamin bahawa semua data akan bersesuaian dengan kuadrat dan minimum. Untuk prinsipnya, kita akan lihat bagaimana menggunakan alat ini untuk mengira a dan b.

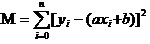
Sekarang, apa yang kita akan lakukan ialah mencari a dan b yang paling kecil bagi M. Perhatikan bahawa dalam persamaan ini, kita sudah tahu y dan xi.

Jadi persamaan ini adalah fungsi binari dengan a, b sebagai pembolehubah, dan M sebagai pembolehubah faktor.

Bayangkan bagaimana fungsi satuan dalam bilangan tinggi mempunyai nilai ekstrem. Kita menggunakan alat derivatif. Dalam fungsi duaan, kita masih menggunakan derivatif. Hanya derivatif di sini mempunyai nama baru, iaitu derivatif bias. Dengan mencari derivatif pada M, kita dapat satu set persamaan.

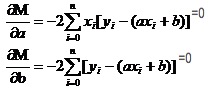
Dalam kedua-dua persamaan ini, x dan y diketahui.

Ia adalah mudah untuk mencari a dan b. Oleh kerana data yang digunakan adalah dari Wikipedia, saya akan teruskan dengan jawapan untuk melukis gambar yang sesuai:

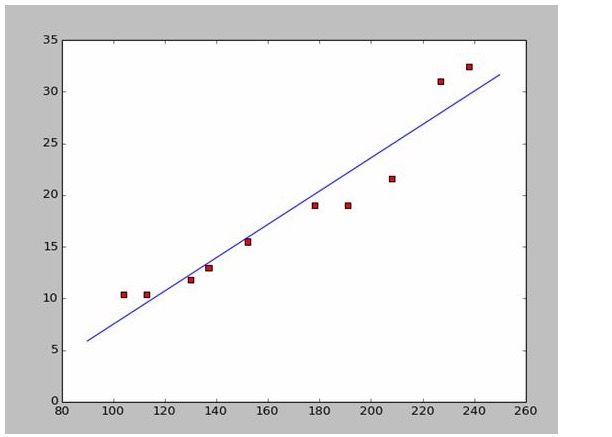
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Empat Prinsip Penyelidikan

Dalam penyesuaian data, mengapa anda perlu membuat perkadaran perbezaan antara data ramalan model dengan data sebenar dan bukannya nilai mutlak dan minimum untuk mengoptimumkan parameter model?

Soalan ini telah dijawab, lihat pautan http://blog.sciencenet.cn/blog-430956-621997.html

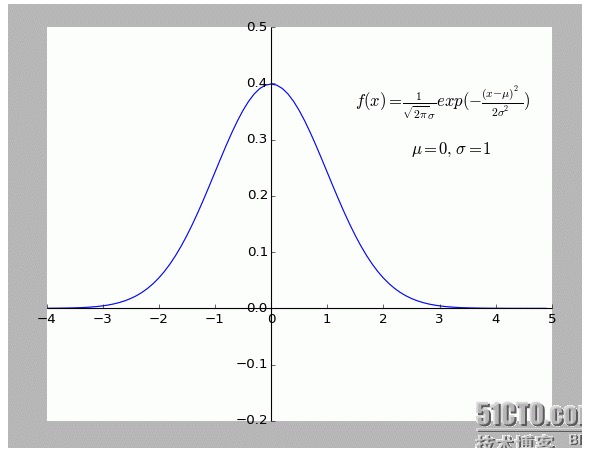
Secara peribadi, saya mendapati penjelasan ini sangat menarik. Terutama hipotesis di dalamnya: semua titik yang menyimpang dari f (x) adalah bising.

Semakin jauh satu titik daripada bunyi, semakin kecil kebarangkalian ia akan muncul. Jadi, apakah hubungan antara tahap penyimpangan x dan kebarangkalian f (x) yang dipenuhi?

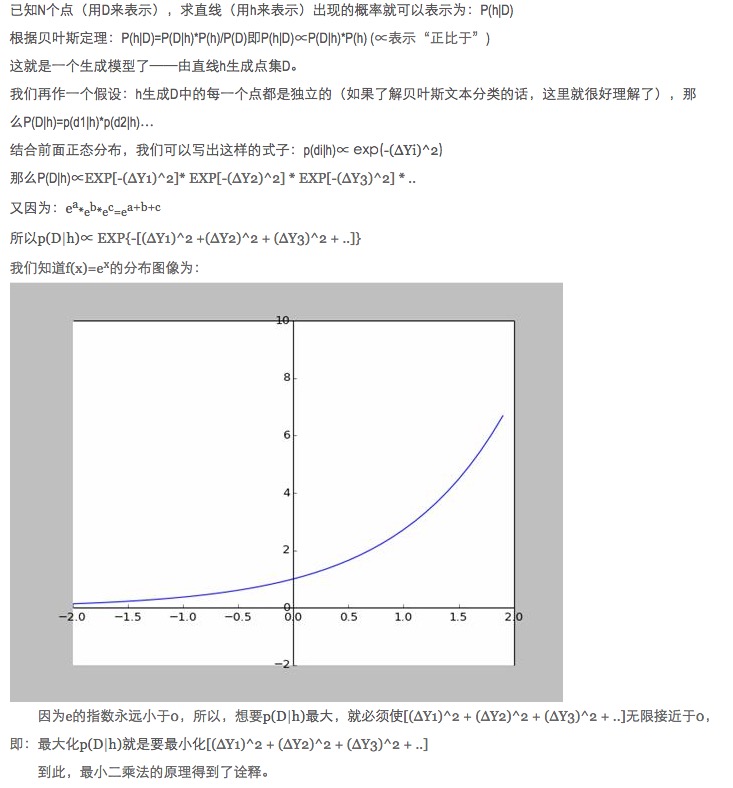
• ### Lima, memperluaskan.

Yang disebutkan di atas adalah keadaan dua dimensi, iaitu hanya ada satu pembolehubah diri. Tetapi dalam dunia nyata, yang mempengaruhi hasil akhir adalah perpaduan pelbagai faktor, iaitu pembolehubah diri akan mempunyai beberapa keadaan.

Untuk fungsi metaliteral N umum, menggunakan matriks terbalik dalam aljabar linier bercabang adalah OK; kerana tidak ada contoh yang sesuai untuk sementara waktu, sebagai argumen, tinggal di sini.

Sudah tentu, alam semula jadi lebih kepada kesesuaian polimer daripada kesesuaian linear yang mudah, yang merupakan sesuatu yang lebih tinggi.

• Rujukan

  • Buku Matematika Tinggi (Edisi Keenam)
  • Aljabar linier berjalur (Beijing University Press)
  • Ensiklopedia interaktif:Perkalian kedua terkecil
  • Wikipedia: Perkalian dua terkecil
  • Rangkaian Sains:Minimum dua kali ganda? Nilai mutlak yang baik untuk kuda Tuhan

Karya asal, izin untuk dipindahkan, apabila dipindahkan, sila pastikan anda menamakan sumber asal artikel dalam bentuk pautan hyperlink, maklumat pengarang dan pernyataan ini. Jika tidak, anda akan bertanggungjawab secara sah. http://sbp810050504.blog.51cto.com/2799422/1269572