Regressão linear - método dos mínimos quadrados

• ### Introdução

Durante esse tempo, o aprendizado da máquina de aprendizagem de pivô e aprendizagem de pivôes de regressão logística do capítulo 5 foi bastante difícil. O processo de retrospecção, da pivôes de regressão logística à pivôes de regressão linear e, em seguida, à pivôes de regressão de pivôes. O módulo de menor quadruplicidade é uma implementação para a construção de fórmulas experimentais em problemas de otimização. Conhecer o seu princípio é útil para entender o módulo de regressão logística e o módulo de aprendizagem de máquinas vetoriais de suporte de módulo.

• ### II. Conhecimento básico

O contexto histórico para o surgimento da fração de minúsculo segundo é interessante.

Em 1801, o astrônomo italiano Giuseppe Piazzi descobriu o primeiro asteroide Ceres. Após 40 dias de observações de rastreamento, Piazzi perdeu a localização de Ceres devido à sua rotação para trás do Sol. Os cientistas do mundo todo começaram a procurar Ceres com os dados de observação de Piazzi, mas não conseguiram encontrar Ceres com base nos resultados calculados pela maioria das pessoas. Gauss, que tinha 24 anos na época, também calculou a órbita de Ceres.

O método usado por Gauss para a multiplicação de mínimos dois foi publicado em 1809 em seu livro A teoria do movimento dos corpos celestes, enquanto o cientista francês Le Gend independentemente descobriu a multiplicação de mínimos dois em 1806, mas não foi divulgado porque não era conhecido. Houve uma disputa sobre quem foi o primeiro a criar o princípio da multiplicação de mínimos dois.

Em 1829, Gauss forneceu uma prova de que o efeito de otimização da multiplicação de mínimos dois é maior do que o de outros métodos, veja o Teorema de Gauss-Markov.

• ### 3o, o uso do conhecimento.

O núcleo da função de Potência Minima Biperiodicidade é garantir o quadrado de todos os dados de desvio e o mínimo. (O nome antigo de Potência Quadrada é Potência Biperiodicidade)

Suponhamos que temos dados de comprimento e largura de alguns navios de guerra.

Com base nesses dados, desenhamos um mapa de pontos dispersos em Python:

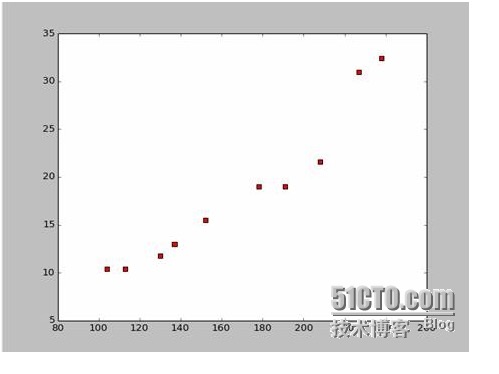
O código para desenhar o mapa de pontos é o seguinte:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Se nós pegamos os dois primeiros pontos, 238, 32, 4 e 152, 15, 5 e temos duas equações. 152*a+b=15.5 328*a+b=32.4 Então vamos resolver essas duas equações e vamos ter a = 0,197 e b = -14,48. A partir daí, podemos obter um mapa de correspondência como este:

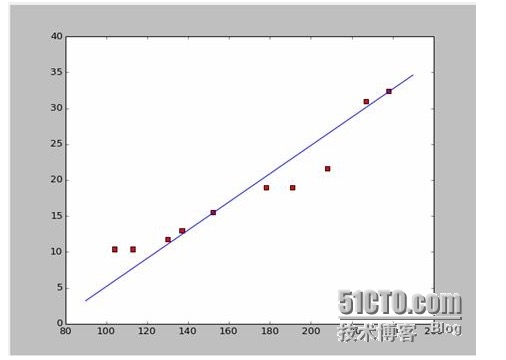
Bem, a nova questão é se a e b são as melhores soluções. A forma mais prática de dizer isso é: a e b são os melhores parâmetros do modelo?

A resposta é: o quadrado e o mínimo de todas as diferenças de dados. Quanto ao princípio, veremos mais adiante como usar esta ferramenta para calcular o melhor a e b.

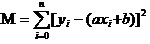
Agora o que vamos fazer é encontrar o mínimo de a e b de M. Observe que, nesta equação, já sabemos que

Então essa equação é uma função binária com a variável a, b, M como variável causa.

Lembre-se de como a função univariável em números elevados tem um valor extremo. Nós usamos a ferramenta da derivada. Então, na função binária, nós ainda usamos derivativos. Só que aqui a derivada tem um novo nome: derivada parcial. Então, quando nós pedimos a derivada parcial de M, nós temos um conjunto de equações.

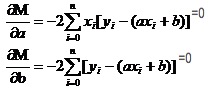
Em ambas as equações, os valores de xi e de y são conhecidos.

É muito fácil encontrar a e b. Como os dados são da Wikipedia, eu uso as respostas aqui para desenhar uma imagem de correspondência:

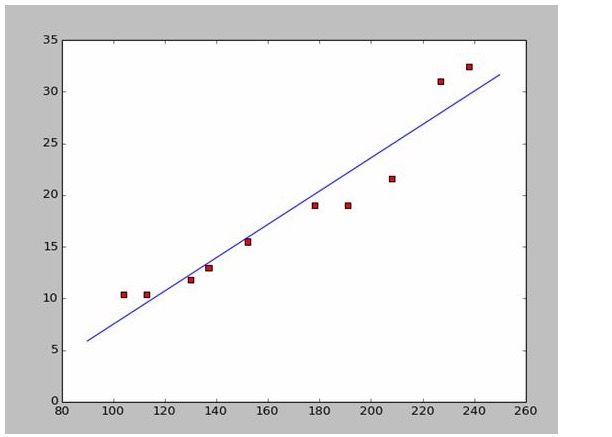
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Quatro Princípios e Investigação

Em data matching, por que o modelo deve ter o quadrado da diferença entre os dados de previsão do modelo e os dados reais em vez de valores absolutos e mínimos para otimizar os parâmetros do modelo?

Esta pergunta já foi respondida, veja o link (http://blog.sciencenet.cn/blog-430956-621997.html)

Eu acho muito interessante essa explicação. Especialmente a hipótese: todos os pontos que se desviam de f (x) são ruidosos.

Quanto mais longe um ponto de desvio, maior o ruído, menor a probabilidade de ocorrência desse ponto. Então, qual é a relação entre o grau de desvio x e a probabilidade de ocorrência f (x)?

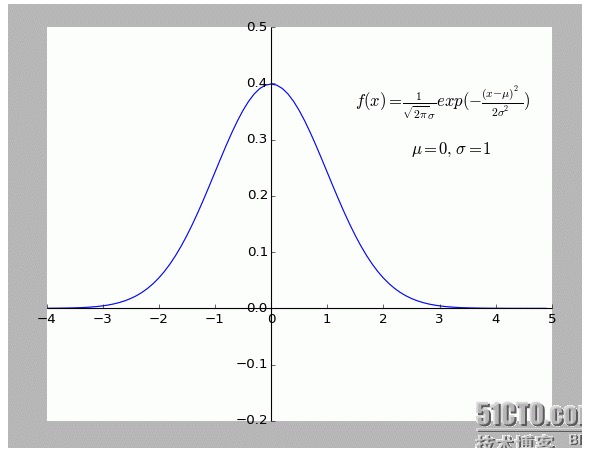
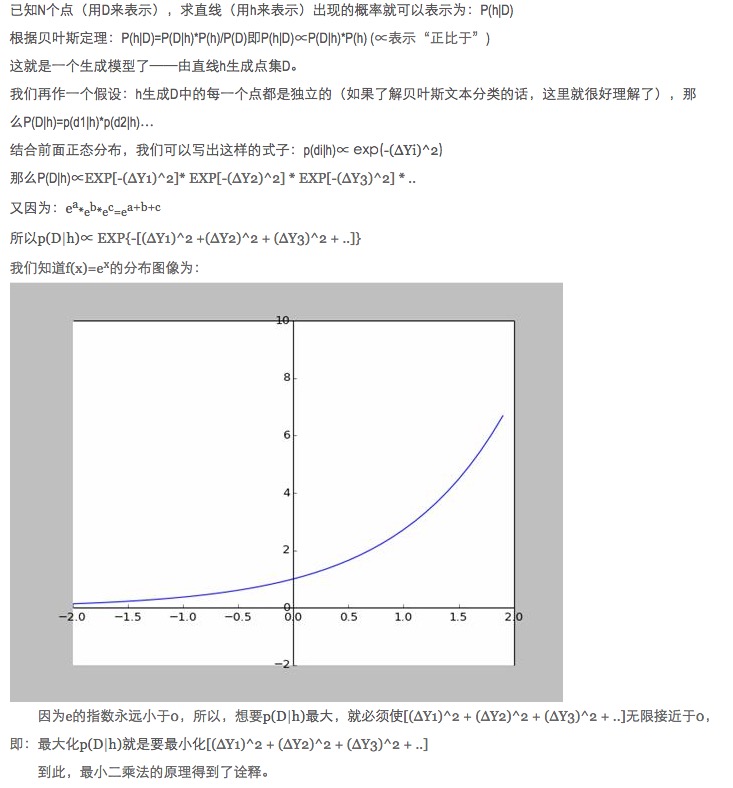
• ### Cinco, expandir.

O que foi dito acima é uma situação bidimensional, ou seja, há apenas uma variável automática. Mas no mundo real, o resultado final é influenciado pela superposição de vários fatores, ou seja, há várias variáveis automáticas.

Para uma função metalinha N em geral, a matriz inversa da cadeia de álgebra linear é aceitável; como não foi encontrado um exemplo apropriado por enquanto, é deixado aqui como um indício.

Claro que a natureza é mais uma adequação polinomial do que uma simples linearidade, que é um conteúdo mais avançado.

• Referências

  • Mestrado em Matemática Superior (Sexta Edição)
  • Aritmética de álgebra linear (Publicado pela Universidade de Pequim)
  • Enciclopédia Interativa:Minimum quadratico
  • Wikipedia: A multiplicação pelo mínimo
  • Rede Científica:O mínimo do quadrado? Um valor absoluto que não é mau para os cavalos de Deus

Obras originais, permitindo a transcrição, transcrição, por favor, certifique-se de indicar a fonte original do artigo, a informação do autor e esta declaração. Senão, será legalmente responsável. http://sbp810050504.blog.51cto.com/2799422/1269572