Линейная регрессия - метод наименьших квадратов

• Введение

  За это время я выучил математику, и мне показалось довольно сложным выучить логистическую регрессию, описанную в главе 5. Я начал изучать логистическую регрессию, затем линейную регрессию, а затем наименьшую двойную степень. В итоге я выучил математику, описанную в главе 9, главе 10 в главе 9 в главе 10 в главе 9 в главе 10 в главе 9 в главе 10 в главе 10 в главе 9 в главе 10 в главе 9 в главе 10 в главе 10 в главе 9 в главе 10 в главе 9 в главе 10 в главе 10 в главе 9 в главе 10 в главе 9 в главе 10 в главе 10 в главе 10 в главе 9 в главе 10 в главе 10 в главе 10 в главе 10 в главе 10 в главе 10 в главе 10 в главе 10 в главе 9 в главе 10 в главе 10 в главе 9 в главе 10 в главе 10 в главе 10 в главе 10 в главе
  Ключ наименьшего двоичного множителя является одним из способов создания экспериментальной формулы в задаче оптимизации. Понимание его принципов полезно для понимания логистической регрессии ключа и обучения ключа, поддерживающего векторную машину ключа.

• Второе: знания о происхождении

  Исторический контекст появления кристаллов наименьшего двоичного множителя очень интересен.

  В 1801 году итальянский астроном Джузепп Пиацци обнаружил первый астероид Стрелец. После 40 дней наблюдений Пиацци потерял его местоположение из-за того, что Стрелец двигался позади Солнца. Впоследствии ученые по всему миру начали искать Стрелец, используя данные наблюдений Пиацци, но не смогли найти его в соответствии с результатами большинства людей.

  Метод наименьшего двоичного умножения, использованный Гаусом, был опубликован в 1809 году в его книге "Теория движения небесных тел", в то время как французский ученый Лежанд в 1806 году самостоятельно обнаружил наименьшее двоичное умножение, но молча не узнал об этом из-за того, что оно не было известно в то время.

  В 1829 году Гаус предоставил доказательство, что оптимизация метода наименьшего двоичного умножения более эффективна, чем другие методы, см. Теорему Гауса-Маркова.

• Использование знаний

  Ядром теории наименьшего двоичного числа является то, что она гарантирует, что все данные являются квадратными и наименьшими.

  Предположим, что мы собираем данные о длине и ширине кораблей.

  

  На основе этих данных мы создали рассеянную карту на языке Python:

  

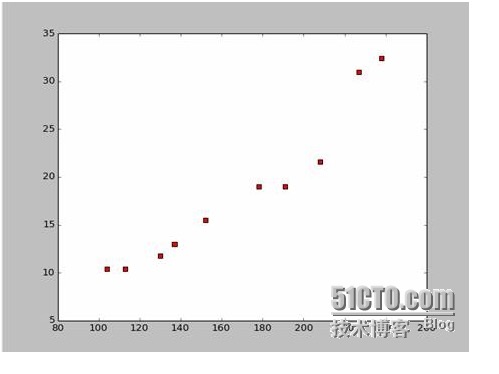
  Код для рассеянной карты выглядит так:

  
              
              
              
  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()
  

  Если мы возьмем первые две точки, то получим два уравнения.
  152a+b=15.5
  328a+b=32.4
  Вы можете решить эти два уравнения, и вы получите a = 0,197, b = -14,48.
  В этом случае мы получим аналогичную карту:

  

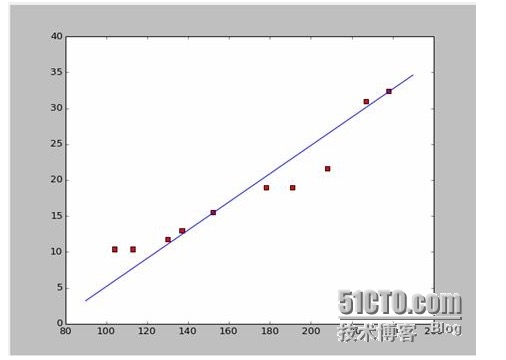
  Новый вопрос: а, b является оптимальным решением? Если говорить профессионально: а, b является оптимальным параметром модели? Прежде чем ответить на этот вопрос, мы должны решить другой вопрос: какие условия a, b должны быть наилучшими?

  Ответ: гарантированный квадрат и минимум всех отклонений данных. Что касается принципов, мы поговорим о них позже, но сначала посмотрим, как использовать этот инструмент, чтобы наилучшим образом рассчитать a и b. Предположим, что сумма квадратов всех данных равна M.

  

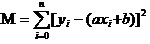
  Теперь нам нужно найти наименьшие a и b в M. Обратите внимание, что в этом уравнении мы знаем, что y и xi

  В данном случае это уравнение представляет собой двоичную функцию, где a, b являются самостоятельными переменными, а M - коэффициентами.

  Вспомним, как в высоких числах однофазные функции имеют предельные значения. Мы используем инструмент деривативов. В бинарных функциях мы все еще используем деривативы.
  Если мы попросим у M производной, то получим множество уравнений.

  

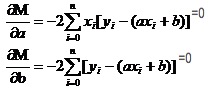
  В обоих уравнениях x и y известны.

  Поскольку мы используем данные из Википедии, я просто использую ответы, чтобы нарисовать соответствующие изображения:

  

  
              
              
              
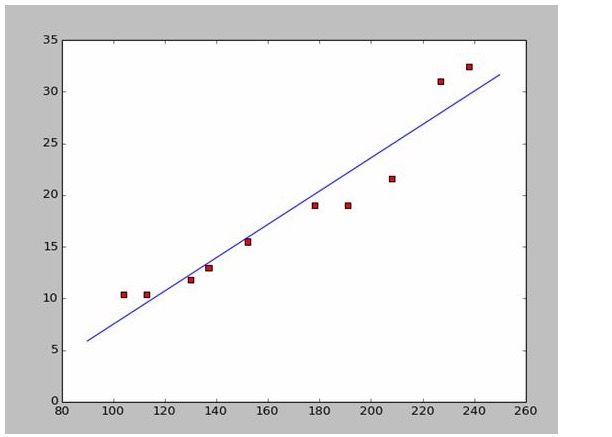
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()
  

• Принципы исследования

  При сопоставлении данных, почему для оптимизации параметров модели используется квадрат отклонения прогнозных данных от фактических данных, а не абсолютные и минимальные значения?

  На этот вопрос уже есть ответ, см. ссылку (http://blog.sciencenet.cn/blog-430956-621997.html)

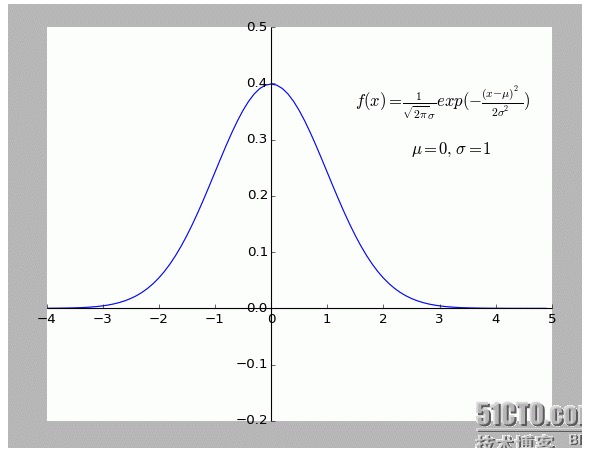
  Лично я нахожу это объяснение весьма интересным. Особенно если учесть, что все точки, отклоняющиеся от f (x), обладают шумом.

  Чем дальше точка отклонения, тем больше вероятность возникновения шума. Какова связь между степенью отклонения x и вероятностью возникновения f (x)?

  

  

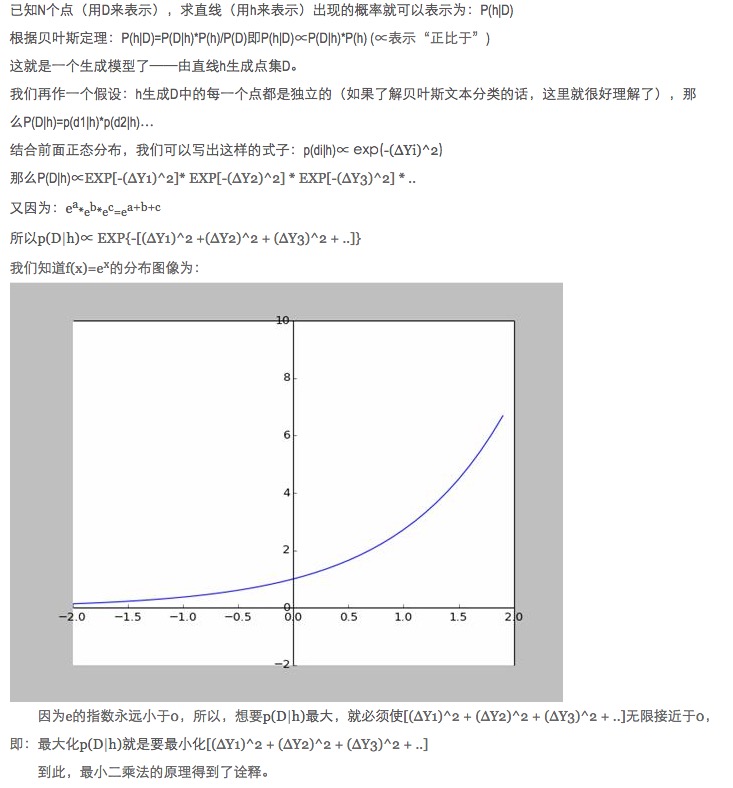
• Пятое: расширение.

  Вышеупомянутые ситуации являются двумерными, то есть существует только одна самостоятельная переменная. Однако в реальном мире влияние на конечный результат оказывает наложение множества факторов, то есть самостоятельная переменная может иметь несколько вариантов.

  Для общего N металинейных функций, использование обратной матрицы в паре линейных алгебраических чисел вполне приемлемо; поскольку пока не найдено подходящего примера, оставляем здесь как аргумент.

  Конечно, в природе больше многообразие, чем просто линейность, то есть более высокий уровень.

• Ссылки

  • Высшее математическое общество (Шестое издание)
  • Линейный алгебраический столб (Пекинское издательство)
  • Интересные фактыМинимальное двоичное умножение
  • Википедия: Минимальное двоичное умножение
  • Научная сеть:Минимальное двоичное умножение?

Оригинальное произведение, разрешенное к копированию, при копировании обязательно укажите в виде гиперссылки источник статьи, информацию об авторе и настоящее заявление. В противном случае будет возложена юридическая ответственность.