لکیری رجعت - کم از کم چوکوں کا طریقہ

• ### پہلا مقدمہ

اس دوران میں نے مشین سیکھنے کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی مشق کی کم سے کم دوگنا فاریکس ٹریڈنگ کیا ہے؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ کم سے کم دوگنا فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ کم سے کم دوگنا فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟

• ### 2، پس منظر

کم سے کم دو ضرب ضرب فاضل کی تاریخ کا پس منظر بہت دلچسپ ہے۔ (مضمون وکی پیڈیا سے ماخوذ ہے)

1801 میں ، اطالوی ماہر فلکیات جوسیپ پیازے نے پہلی چھوٹی سی سیٹلائٹ وادی اسٹار کی دریافت کی۔ 40 دن کی نگرانی کے بعد ، وادی اسٹار سورج کے پیچھے چلنے کی وجہ سے پیازے نے وادی اسٹار کی جگہ کھو دی۔ اس کے بعد ، دنیا بھر کے سائنس دانوں نے پیازے کے مشاہدے کے اعداد و شمار کا استعمال کرتے ہوئے وادی اسٹار کی تلاش شروع کردی ، لیکن زیادہ تر لوگوں کے حساب سے وادی اسٹار کی تلاش میں کوئی نتیجہ نہیں نکلا۔ اس وقت 24 سالہ گاس نے بھی وادی اسٹار کی مدار کا حساب لگایا تھا۔ آسٹریا کے ماہر فلکیات ہینریچ اولبرس نے وادی اسٹار کی دوبارہ دریافت کی ، جو اس کے حساب سے ہے۔

گوس نے کم سے کم دو ضرب کے طریقہ کار کو 1809 میں اپنی کتاب میں شائع کیا تھا جس میں کائنات کی حرکت کی تھیوری تھی ، اور فرانسیسی سائنس دان لیجینڈ نے 1806 میں آزادانہ طور پر کم سے کم دو ضرب کا اصول دریافت کیا تھا ، لیکن اس وقت کے لئے جانا جاتا نہیں تھا۔ دونوں نے اس بات پر تنازعہ کیا تھا کہ کم سے کم دو ضرب کا اصول سب سے پہلے کس نے بنایا تھا۔

1829 میں، گاسس نے یہ ثبوت فراہم کیا کہ کم سے کم دو ضرب کا اصلاحی اثر دیگر طریقوں سے زیادہ مضبوط ہے، دیکھیں گاسس-مارکوف تھیوریم۔

• ### تیسرا، علم کا استعمال

کم سے کم دو ضرب ضرب ضرب ضرب کا بنیادی مقصد یہ ہے کہ تمام اعداد و شمار کے انحراف کا مربع اور کم سے کم ہو۔ (قدیم زمانے میں مربع ضرب ضرب ضرب کو دو ضرب ضرب ضرب کہا جاتا تھا)

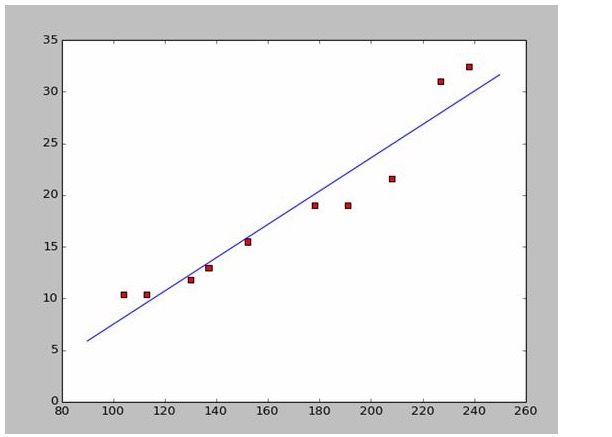
اگر ہم کچھ جہازوں کی لمبائی اور چوڑائی کے اعداد و شمار جمع کرتے ہیں

ہم نے ان اعداد و شمار کے مطابق پائیتھون میں ایک پراکسی نقشہ تیار کیا ہے:

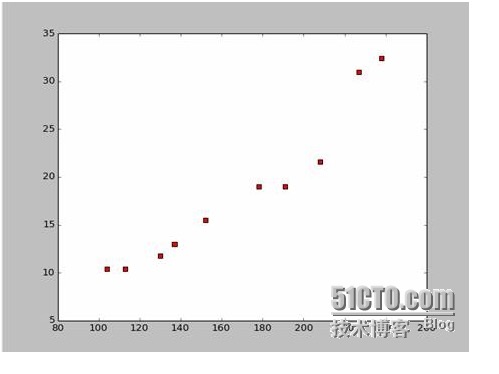
اسکرین شاٹ کے لیے کوڈ درج ذیل ہے:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

اور اگر ہم پہلے دو پوائنٹس کو لے لیں، 238،32،4،152،15،5، تو ہم دونوں مساوات حاصل کر سکتے ہیں. 152*a+b=15.5 328*a+b=32.4 اور پھر ہم ان دونوں مساوات کو حل کرتے ہیں، اور ہم کہتے ہیں کہ a=0.197، اور b=-14.48 اس طرح، ہم اس طرح کی ایک انضمام گراف حاصل کر سکتے ہیں:

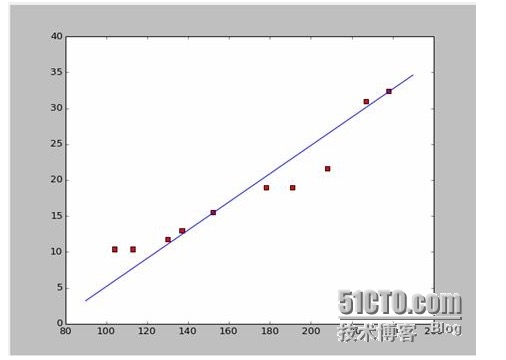
ٹھیک ہے، اب سوال یہ ہے کہ کیا a اور b بہترین حل ہیں؟ اگر ہم اسے پیشہ ورانہ انداز میں بیان کریں تو کیا a اور b ماڈل کے بہترین پیرامیٹرز ہیں؟ اس سوال کا جواب دینے سے پہلے، ہم ایک اور سوال کو حل کریں گے: a اور b کون سی شرائط پر پورا اترتے ہیں جو بہترین ہیں؟

اس کا جواب یہ ہے کہ: تمام اعداد و شمار کا مربع اور کم سے کم ضابطہ کو یقینی بنائیں۔ اصول کے بارے میں، ہم بعد میں بات کریں گے، پہلے دیکھیں گے کہ اس ٹول کا استعمال کیسے کیا جائے تاکہ بہترین a اور b کا حساب لگایا جا سکے۔ فرض کریں کہ تمام اعداد و شمار کا مربع مجموعہ M ہے،

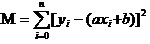
اب ہم M کے سب سے چھوٹے a اور b کو تلاش کریں گے۔ نوٹ کریں کہ اس مساوات میں ہم نے y اور xi کو پہلے ہی جان لیا ہے۔

تو یہ مساوات ایک دوہری فنکشن ہے جس میں a، b خود متغیر ہیں اور M اس کی وجہ متغیر ہے۔

سوچیں کہ کس طرح اعلی اعداد میں ایک متغیر کے لئے افادیت ہے۔ ہم ڈائریکٹر کا آلہ استعمال کرتے ہیں۔ تو دوہری فنکشن میں ، ہم اب بھی ڈائریکٹر استعمال کرتے ہیں۔ صرف یہاں ڈائریکٹر کا نیا نام ہے ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر ڈائریکٹر M کے لئے اس کی derivatives کی طرف سے، ہم مساوات کی ایک سیٹ حاصل

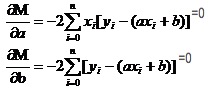
ان دونوں مساوات میں xi اور yi دونوں کو معلوم ہے۔

یہ آسان ہے کہ a اور b کو تلاش کیا جائے۔ ویکیپیڈیا کے اعداد و شمار کو استعمال کرتے ہوئے، میں یہاں براہ راست جوابات کا استعمال کرتا ہوں تاکہ ایک مناسب تصویر کھینچی جا سکے:

  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### چار اصول، دریافت

اعداد و شمار کے ملاپ میں ، ماڈل پیرامیٹرز کو بہتر بنانے کے لئے مطلق اور کم سے کم کے بجائے ماڈل کے پیش گوئی شدہ اعداد و شمار کو اصل اعداد و شمار کے فرق کے مربع کیوں دیا جائے؟

اس سوال کا جواب پہلے ہی دیا جا چکا ہے، لنک ملاحظہ کریں:

ذاتی طور پر اس وضاحت کو بہت دلچسپ پایا گیا ہے۔ خاص طور پر اس میں یہ مفروضہ ہے کہ f (x) سے ہٹ جانے والے تمام پوائنٹس شور مچا رہے ہیں۔

ایک نقطہ سے جتنا دور ہو جائے گا ، اس کا مطلب ہے کہ شور جتنا زیادہ ہوگا ، اس نقطہ کا امکان بھی اتنا ہی کم ہوگا۔ تو پھر انحراف کی سطح x اور اس کا امکان f ((x) کیا ہے؟

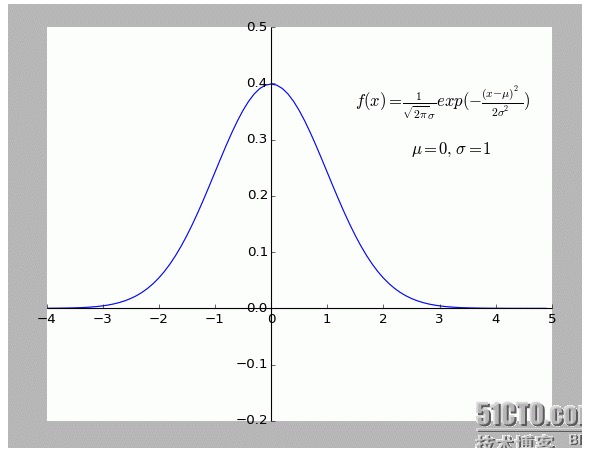
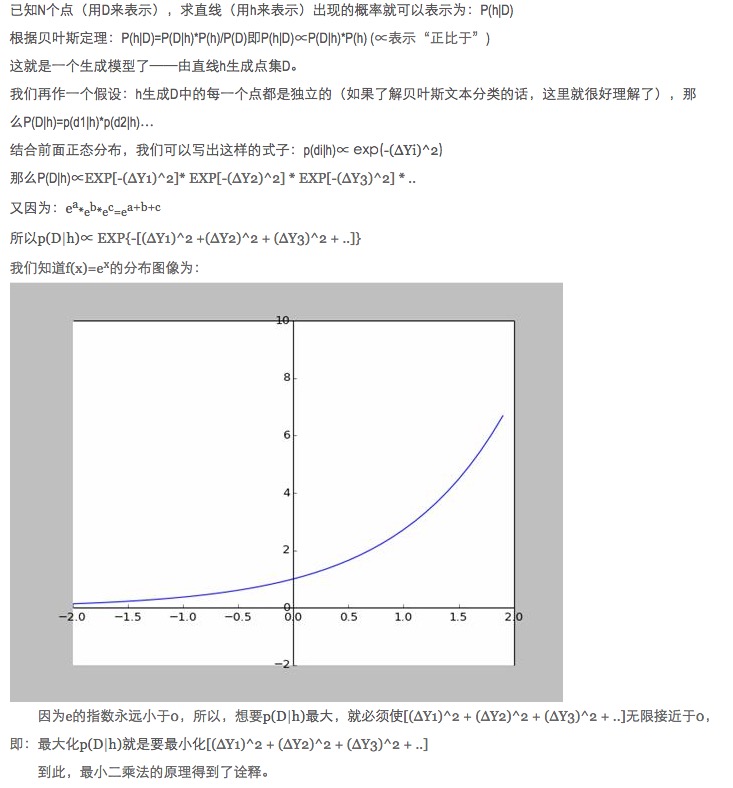
• ### پانچواں: توسیع

مذکورہ بالا دو جہتی صورت حال ہے ، یعنی صرف ایک خود متغیر ہے۔ لیکن حقیقی دنیا میں حتمی نتائج پر اثر انداز ہونے والے متعدد عوامل کا ایک دوسرے پر اثر پڑتا ہے ، یعنی خود متغیر کی ایک سے زیادہ صورت حال ہوگی۔

عام طور پر N میٹالینیئر فنکشن کے لئے ، کالمینیئر الجبرا کی سلاخوں میں ریورس میٹرکس کے ساتھ حل تلاش کرنا ٹھیک ہے۔ چونکہ ابھی تک کوئی مناسب مثال نہیں ملی ہے ، لہذا ایک اشارہ کے طور پر ، یہاں چھوڑ دیا گیا ہے۔

یقیناً فطرت میں ایک سادہ سی لکیری نہیں بلکہ ایک کثیر جہتی انضمام ہے، جو کہ ایک اعلی درجے کی چیز ہے۔

• حوالہ جات

  • اعلی ریاضی (چھٹا ایڈیشن) اعلی تعلیم پبلشر)
  • بیجنگ یونیورسٹی پبلشنگ)
  • انٹرایکٹو انسائیکلوپیڈیا:کم سے کم دوگنا
  • ویکیپیڈیا: کم سے کم دو ضرب
  • سائنس نیٹ:کم سے کم دوگنا کیا ہے؟

اصل کام ، نقل و حمل کی اجازت ، نقل و حمل کے وقت ہائپر لنک کی شکل میں مضمون کی اصل ذریعہ ، مصنف کی معلومات اور اس بیان کی نشاندہی کریں۔ ورنہ قانونی ذمہ داری کا سامنا کرنا پڑے گا۔http://sbp810050504.blog.51cto.com/2799422/1269572