1
关注
1815
关注者
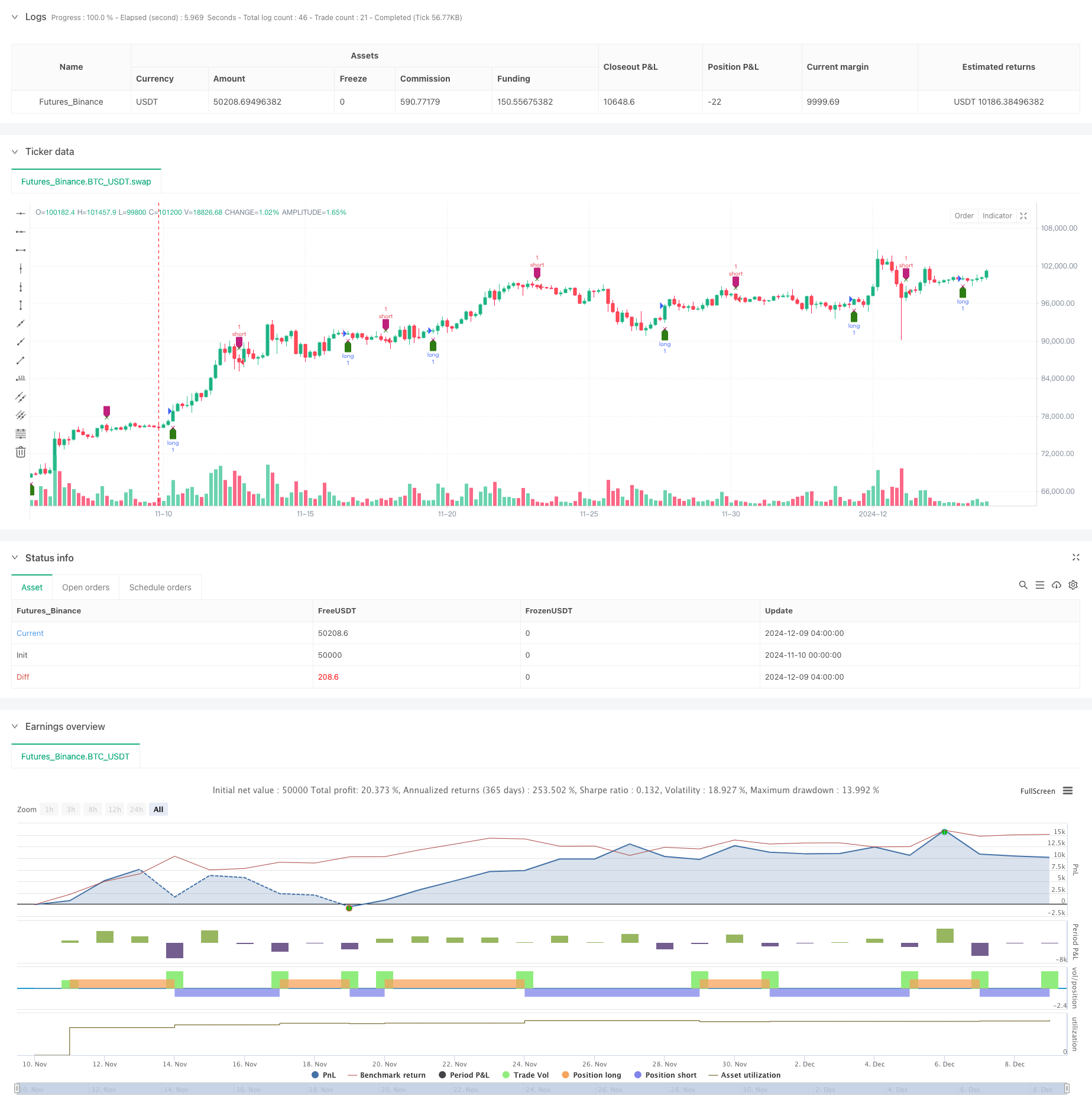
该策略是一个基于RSI动态振荡器的量化交易系统。通过对RSI指标进行多项式拟合和时间序列分析,计算RSI的变化率来捕捉市场动量。策略采用QR分解等高级数学方法进行信号处理,并结合均线系统进行交易决策。
策略原理
策略的核心是Delta-RSI震荡器,它通过以下步骤实现:
- 首先计算传统RSI指标作为基础数据
- 使用多项式拟合对RSI进行平滑处理,减少噪声
- 计算RSI的时间导数得到Delta-RSI,反映RSI的变化速率
- 将Delta-RSI与其移动平均线比较生成交易信号
- 使用均方根误差(RMSE)对拟合质量进行评估和过滤
交易信号可以通过三种方式产生:
- 零线穿越:Delta-RSI从负值转正时做多,从正值转负时做空
- 信号线交叉:Delta-RSI上穿/下穿其移动平均线时分别做多/做空
- 方向改变:Delta-RSI在负值区域开始上升时做多,在正值区域开始下降时做空
策略优势
- 数学基础扎实：采用QR分解等高级数学方法进行信号处理,理论基础可靠
- 信号平滑：多项式拟合可以有效过滤市场噪声,提高信号质量
- 灵活性强：提供多种信号生成方式和参数选择,适应不同市场环境
- 风险可控：包含RMSE过滤机制,可以筛选出可靠性较高的信号
- 计算高效：矩阵运算采用优化算法,运行效率较高
策略风险
- 参数敏感：多个关键参数需要精心调整,参数选择不当会严重影响策略表现
- 滞后性：信号平滑处理会带来一定滞后,可能错过快速行情
- 假突破：在震荡市场中可能产生虚假信号,增加交易成本
- 计算复杂：涉及较多矩阵运算,在高频交易中可能存在性能瓶颈
- 过度拟合：参数优化时需要注意避免过度拟合历史数据
策略优化方向
- 自适应参数：可以根据市场波动率动态调整RSI周期和拟合阶数
- 多时间周期：结合更多时间周期的信号进行交叉验证
- 波动率过滤：加入ATR等波动率指标进行信号过滤
- 市场分类：针对不同市场状态(趋势/震荡)使用不同的信号生成规则
- 止损优化：加入更智能的止损机制,如基于支撑阻力位的动态止损
总结
这是一个结构完整、理论基础扎实的量化交易策略。通过对RSI的动态特性分析,结合现代数学方法进行信号处理,能够较好地捕捉市场趋势。虽然存在一定的参数敏感性和计算复杂度问题,但通过合理的参数选择和优化改进,该策略具有良好的应用价值。建议在实盘应用时注意风险控制,合理设置仓位,并持续监控策略表现。
策略源码
Pine
/*backtest
start: 2024-11-10 00:00:00
end: 2024-12-09 08:00:00
period: 4h
basePeriod: 4h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © tbiktag
//
// Delta-RSI Oscillator Strategy策略参数
评论
全部评论 (0)
暂无数据
- 1