Bitte beachten Sie, dass dieser Fall nur für die Zwecke der Lernforschung und nicht als Investitionsempfehlung dient.

Die Bitcoin-Preisdaten basieren auf einer Zeitreihenfolge, so dass die meisten Bitcoin-Preisprognosen mit dem LSTM-Modell durchgeführt werden.

Langzeit-Kurzzeit-Speicher (LSTM) ist ein Deep-Learning-Modell, das speziell für Zeitreihen-Daten (oder Daten mit einer zeitlichen / räumlichen / strukturellen Reihenfolge, wie z. B. Filme, Sätze usw.) geeignet ist und ideal für die Vorhersage der Kursentwicklung von Kryptowährungen ist.

Dieser Artikel beschäftigt sich hauptsächlich mit der Datensammelung über LSTM, um den zukünftigen Preis von Bitcoin vorherzusagen.

Bibliotheken, die von import benötigt werden

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Datenanalyse

Daten laden

Lesen Sie die Tageshandelsdaten für BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Derzeit sind 1380 Datensätze vorhanden, die sich aus den Spalten Date, Open, High, Low, Close, Volume (BTC), Volume (Currency) und Weighted Price zusammensetzen.

data.info()

Schauen Sie sich die ersten 10 Zeilen an.

data.head(10)

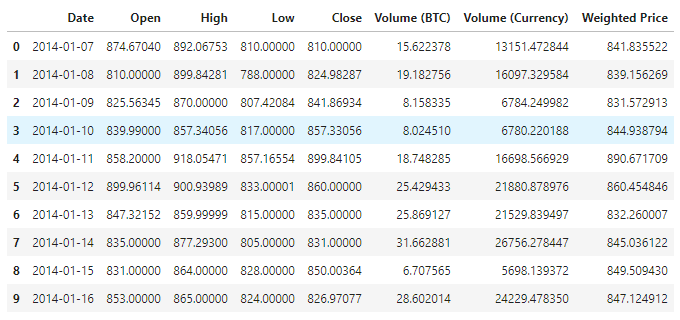
Datenvisualisierung

Mit matplotlib erstellen wir einen Weighted Price, um die Verteilung und Entwicklung der Daten zu sehen. In der Grafik finden wir einen Teil mit Daten 0, und wir müssen feststellen, ob es Ausnahmen gibt.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

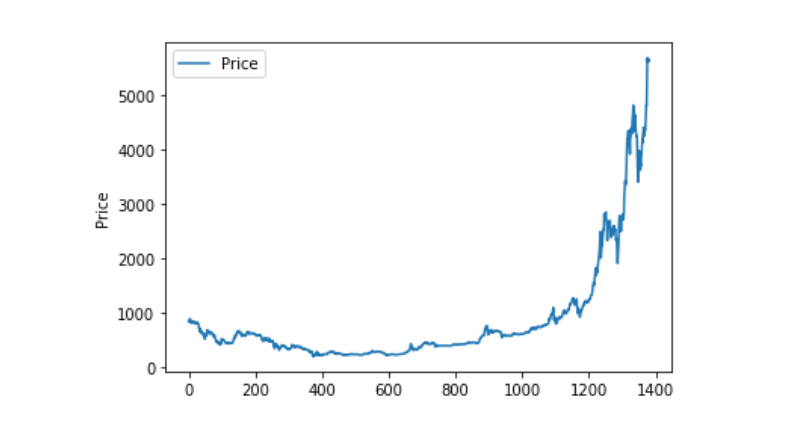
Außergewöhnliche Datenverarbeitung

Wir können sehen, dass es keine Daten von nan gibt, wenn wir sehen, dass es Daten von nan gibt.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Und wenn wir uns die Null-Daten anschauen, dann sehen wir, dass wir Null-Werte in unseren Daten haben, die wir verarbeiten müssen.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Wenn wir die Verteilung und die Entwicklung der Daten betrachten, sehen wir, dass die Kurve sehr kontinuierlich ist.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Trennung von Trainings- und Testdatensätzen

Daten zu 0-1 einheitlich machen

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Test- und Trainingsdatensätze in 2:8 geteilt

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Erstellen von Trainingsdatensätzen und Testdatensätzen, mit einem Tag als Fensterperiode, um unsere Trainingsdatensätze und Testdatensätze zu erstellen.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Modell definieren und trainieren

Diesmal benutzen wir ein einfaches Modell, das wie folgt aufgebaut ist:. LSTM2. Dense。

Input Shape hat die Dimension ((batch_size, time steps, features)). Der Wert von time steps ist der Zeitfensterintervall, in dem die Daten eingegeben werden. Hier verwenden wir 1 Tag als Zeitfenster, und unsere Daten sind Tagesdaten, so dass unsere Zeitschritte hier 1 sind.

Langes Kurzzeitgedächtnis (LSTM) ist ein spezielles RNN, das hauptsächlich zur Lösung von Grad-Verlust und Grad-Blast bei langem Sequenz-Training verwendet wird.

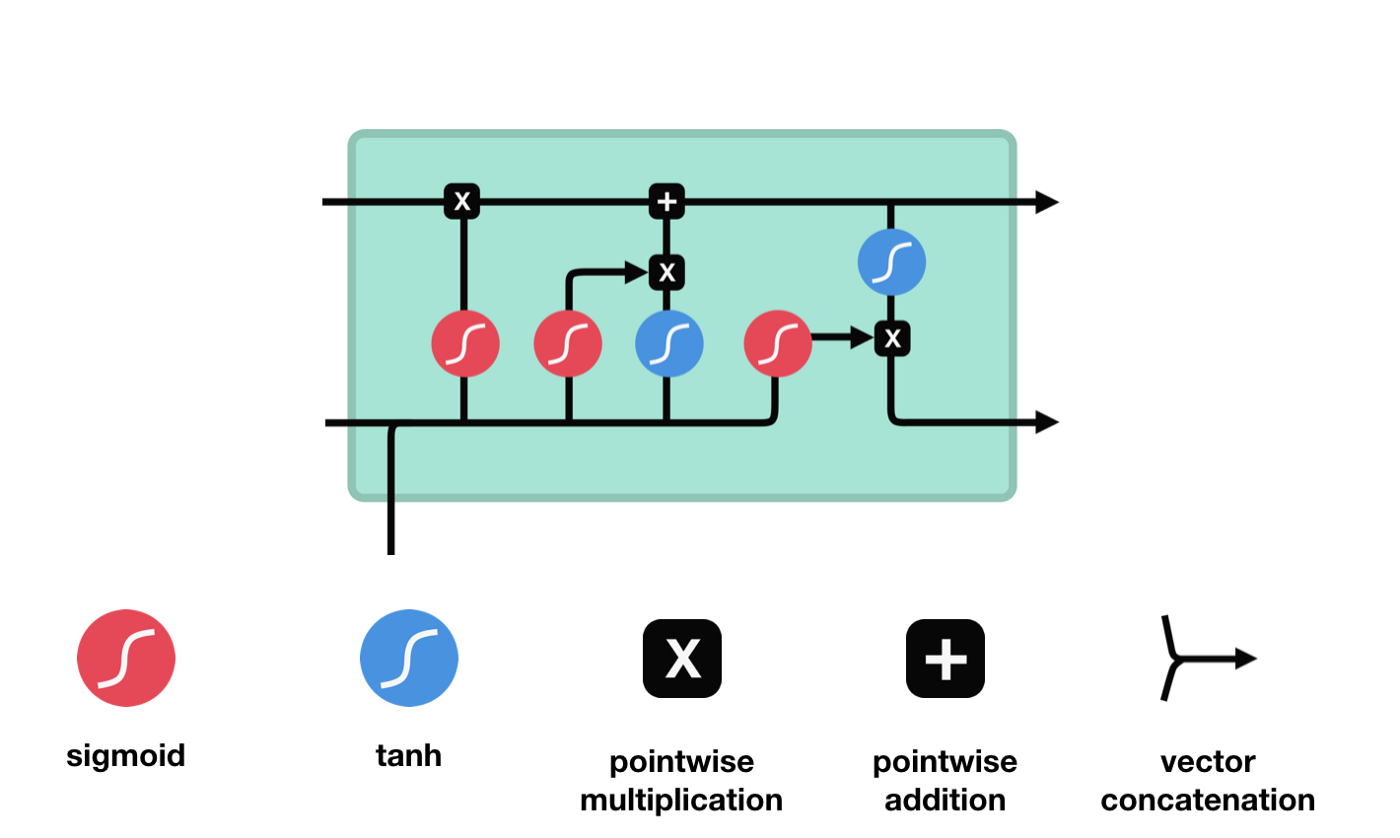
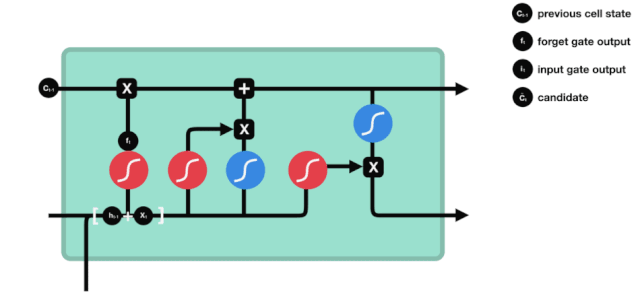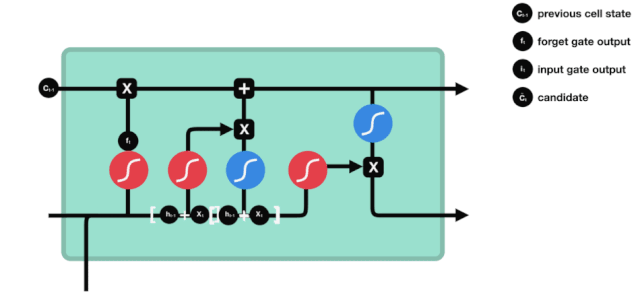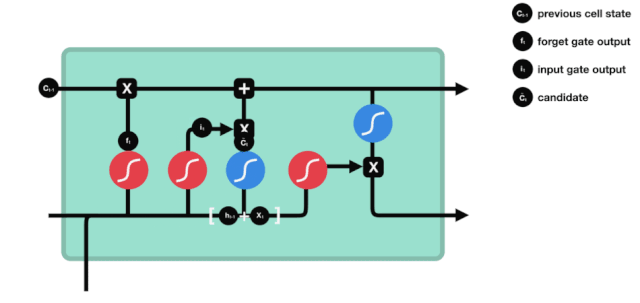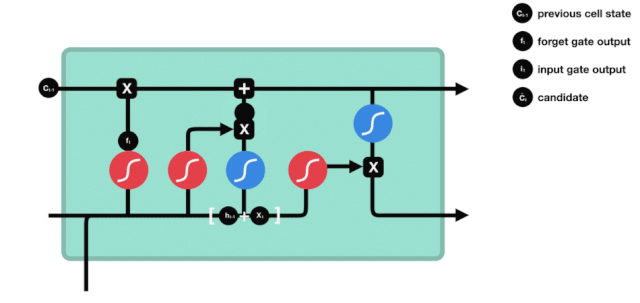
Aus der LSTM-Netzwerkstrukturdiagramm lässt sich erkennen, dass der LSTM ein kleines Modell ist, das drei Sigmoid-Aktivierungsfunktionen, zwei Tanh-Aktivierungsfunktionen, drei Multiplikationen und eine Addition enthält.

Zellstatus

Der Zellzustand ist das Herzstück des LSTM, die oberste schwarze Linie in der Abbildung. Unter dieser schwarzen Linie befinden sich einige Türen, die wir im Folgenden beschreiben. Der Zellzustand wird entsprechend den Ergebnissen jeder Tür aktualisiert.

LSTM-Netzwerke können Informationen über Zellzustände durch eine Struktur, die als Gate bezeichnet wird, entfernen oder hinzufügen. Die Gate kann selektiv entscheiden, welche Informationen durchlaufen dürfen. Die Gate-Struktur ist eine Kombination aus einer Sigmoid-Schicht und einer Punktmultiplikation.

Das Tor der Vergessenheit

Der erste Schritt des LSTM ist die Bestimmung, welche Informationen der Zellzustand entsorgen muss. Dieser Schritt wird von einer Sigmoid-Einheit, der Vergesseneingang, durchgeführt.

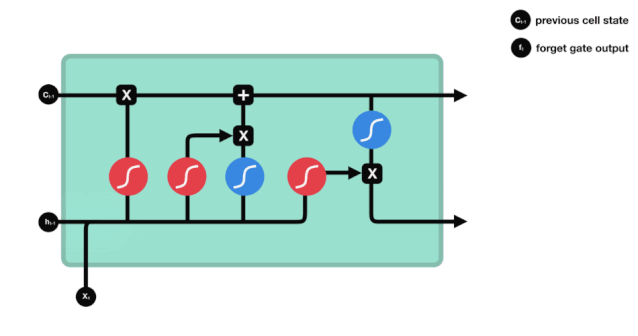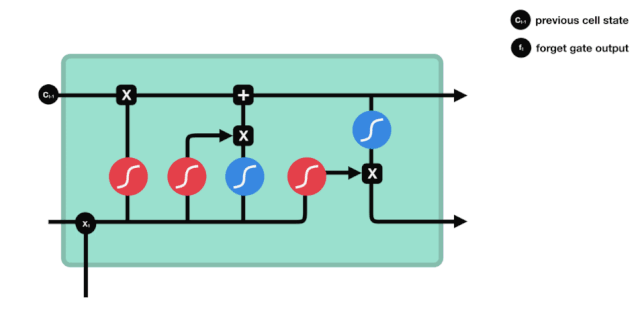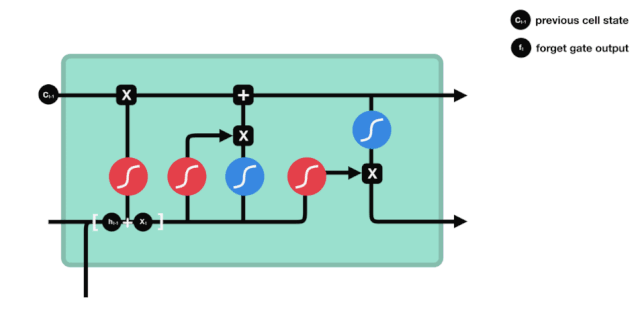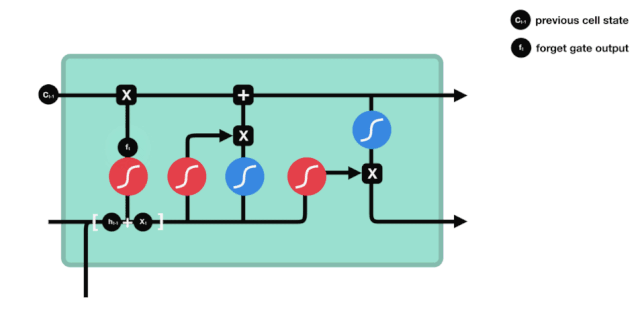
Wir können sehen, dass die Vergessensschranke durch Betrachten der \(h_{l-1}\) und \(x_{t}\) Informationen einen Vektor zwischen 0-1 ausführt, wobei der Wert 0-1 in diesem Vektor anzeigt, welche Informationen in der Zellstatus \(C_{t-1}\) erhalten oder verworfen werden. 0 bedeutet, dass sie nicht gespeichert werden, und 1 bedeutet, dass sie alle gespeichert werden.

Mathematische Ausdrucksweise: \(f_{t} =\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

Eingabe

Der nächste Schritt ist, zu entscheiden, welche neuen Informationen dem Zellstatus hinzugefügt werden, und dieser Schritt wird durch das Öffnen der Eingabetür durchgeführt.

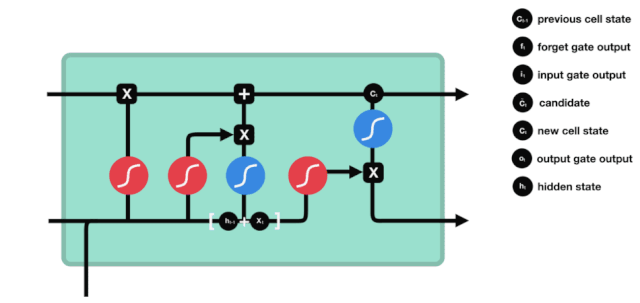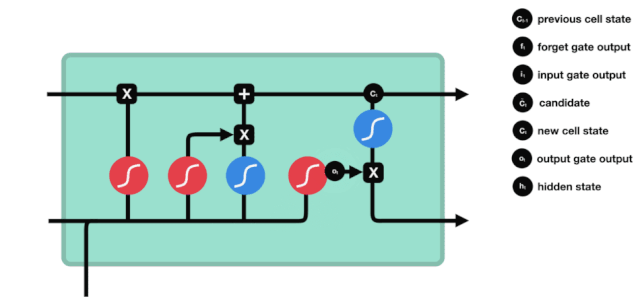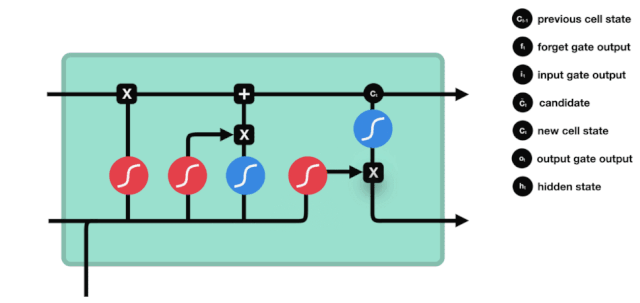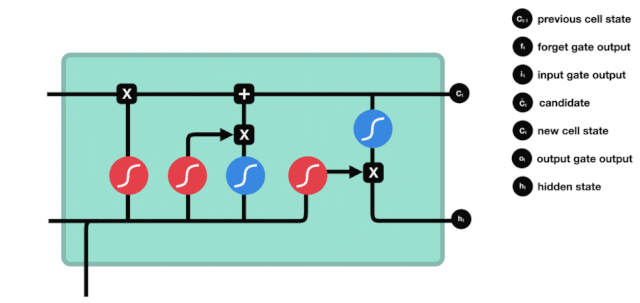
Wir haben gesehen, dass \(h_{l-1}\) und \(x_{t}\) in eine Vergessenheit (sigmoid) und eine Eingabe (tanh) eingefügt wurden. Da die Ausgabe der Vergessenheit 0-1 ist, werden die Ergebnisse der Eingabe \(C_{i}\) nicht in den aktuellen Zellzustand aufgenommen, wenn die Vergessenheit 0 ist, sondern 1, so dass die Funktion der Vergessenheit darin besteht, die Ergebnisse der Eingabe selektiv in den Zellzustand aufzunehmen.

Die mathematische Formel lautet: \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

Ausfahrt

Nach der Aktualisierung des Zellzustands wird die Summe der \(h_{l-1}\) und \(x_{t}\) Eingaben verwendet, um zu bestimmen, welche Zustandseigenschaften der ausgehenden Zelle vorliegen. Die Eingabe wird durch eine Sigmoid-Schicht, die als Ausgangstor bezeichnet wird, beurteilt, und dann wird der Zellzustand durch die Tanh-Schicht mit einem Vektor zwischen -1 und 1 beurteilt. Dieser Vektor und die Ausgangstür werden multipliziert, um den Ausgang der endgültigen RNN-Einheit zu erhalten.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

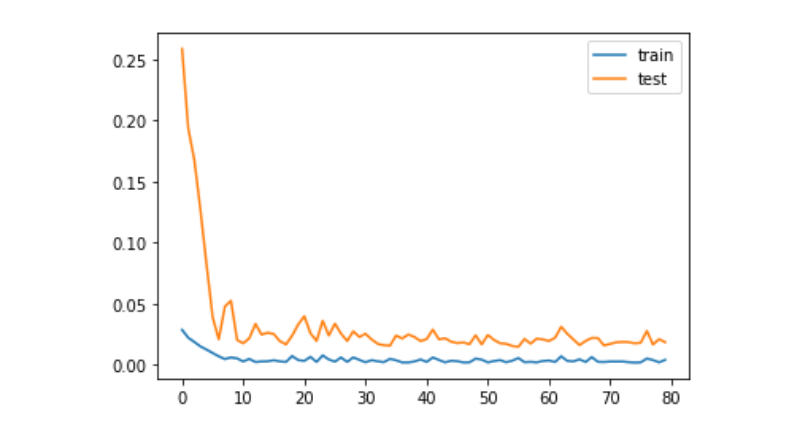
history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Prognose

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

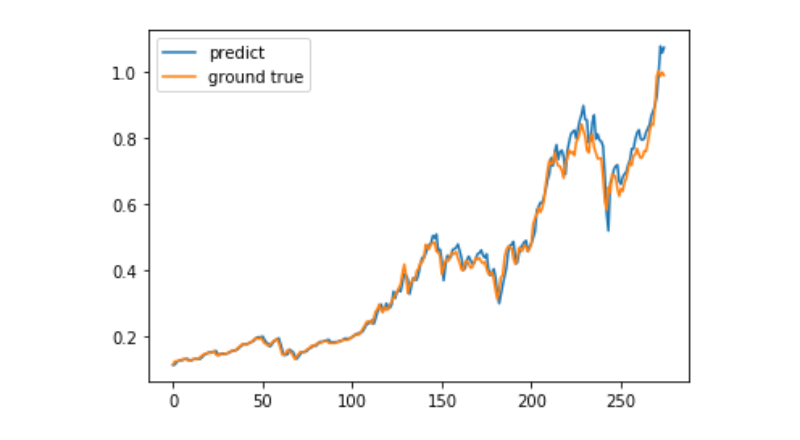
Derzeit ist es sehr schwierig, mit Hilfe von maschinellem Lernen die langfristige Preisentwicklung von Bitcoin zu prognostizieren. Dieser Artikel dient lediglich als Lehrfall. Der Fall wird anschließend mit einer Demo-Image der Matrix-Wolke online gestellt, die interessierte Benutzer direkt erleben können.