En este artículo escribiremos una estrategia de day trading. Utilizará el concepto comercial clásico de “pares comerciales de reversión a la media”. En este ejemplo, utilizaremos dos fondos cotizados en bolsa (ETF), SPY e IWM, que cotizan en la Bolsa de Valores de Nueva York (NYSE) e intentan representar los índices del mercado de valores de EE. UU., el S&P 500 y el Russell 2000. .

La estrategia crea un “carry” al posicionarse en largo con un ETF y en corto con otro. La relación largo-corto se puede definir de muchas maneras, por ejemplo, utilizando métodos de series de tiempo de cointegración estadística. En este escenario, calcularemos la relación de cobertura entre SPY e IWM mediante regresión lineal continua. Esto nos permitirá crear un “spread” entre SPY e IWM que se normaliza a una puntuación z. Cuando el puntaje z excede un cierto umbral, se genera una señal comercial porque creemos que este “spread” volverá a la media.

La razón de esta estrategia es que tanto SPY como IWM representan aproximadamente el mismo escenario de mercado, es decir, el desempeño del precio de las acciones de un grupo de empresas estadounidenses grandes y pequeñas. La premisa es que si se acepta la teoría de la “reversión a la media” de los precios, entonces siempre se revertirá, porque los “acontecimientos” pueden afectar al S&P 500 y al Russell 2000 por separado en un período muy corto de tiempo, pero el “diferencial de tipos de interés” entre ellos siempre volverán a la media normal y las series de precios de largo plazo de ambos siempre estarán cointegradas.

Estrategia

La estrategia se ejecuta de la siguiente manera:

Datos: obtenga gráficos de velas de 1 minuto de SPY e IWM desde abril de 2007 hasta febrero de 2014.

Procesando - Alinear correctamente los datos y eliminar las barras que faltan entre sí. (Si falta un lado, se eliminarán ambos lados)

Spread: la relación de cobertura entre dos ETF se calcula utilizando una regresión lineal continua. Se define como el coeficiente de regresión beta utilizando una ventana retrospectiva que se mueve hacia adelante 1 barra y se recalcula el coeficiente de regresión. Por lo tanto, la relación de cobertura βi, bi K-line se utiliza para trazar la línea K calculando el punto de cruce de bi-1-k a bi-1.

Puntuación Z: el valor del spread estándar se calcula de la forma habitual. Esto significa restar la media del spread (muestra) y dividirla por la desviación estándar del spread (muestra). La razón de hacer esto es hacer que el parámetro de umbral sea más fácil de entender, ya que el puntaje Z es una cantidad adimensional. Introduje intencionalmente un “sesgo de anticipación” en los cálculos para mostrar cuán sutil puede ser. ¡Probar!

Comercio: Las señales largas se generan cuando el valor del puntaje z negativo cae por debajo de un umbral predeterminado (o optimizado posteriormente), mientras que las señales cortas se generan al revés. Cuando el valor absoluto de la puntuación z cae por debajo de un umbral adicional, se genera una señal para cerrar la posición. Para esta estrategia, elegí (de manera algo arbitraria) |z| = 2 como umbral de entrada y |z| = 1 como umbral de salida. Suponiendo que la reversión a la media juega un papel en el spread, lo anterior con suerte capturará esta relación de arbitraje y proporcionará una buena ganancia.

Quizás la mejor manera de comprender profundamente una estrategia es implementarla. La siguiente sección detalla el código Python completo (archivo único) utilizado para implementar esta estrategia de reversión a la media. He agregado comentarios de código detallados para ayudarlo a comprender mejor.

Implementación de Python

Al igual que con todos los tutoriales de Python/pandas, su entorno de Python debe configurarse como se describe en este tutorial. Una vez completada la configuración, la primera tarea es importar las bibliotecas de Python necesarias. Esto es necesario para usar matplotlib y pandas.

Las versiones específicas de la biblioteca que estoy usando son las siguientes:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

Sigamos adelante e importemos estas bibliotecas:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

La siguiente función create_pairs_dataframe importa dos archivos CSV que contienen las velas intradía de dos símbolos. En nuestro caso serían SPY y IWM. Luego crea un “par de marcos de datos” separado que utiliza los índices de ambos archivos originales. Sus marcas de tiempo pueden variar debido a transacciones omitidas y errores. Este es uno de los principales beneficios de utilizar una biblioteca de análisis de datos como pandas. Manejamos código “boilerplate” de una manera muy eficiente.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

El siguiente paso es realizar una regresión lineal continua entre SPY e IWM. En este escenario, IWM es el predictor (‘x’) y SPY es la respuesta (‘y’). Establecí una ventana retrospectiva predeterminada de 100 velas. Como se mencionó anteriormente, estos son los parámetros de la estrategia. Para que una estrategia se considere robusta, lo ideal sería ver un informe de retorno que sea convexo a lo largo del período retrospectivo (o alguna otra medida de desempeño). Por lo tanto, en una etapa posterior del código, realizaremos un análisis de sensibilidad variando el período de retrospección dentro del alcance.

Después de calcular los coeficientes beta móviles en el modelo de regresión lineal para SPY-IWM, agréguelo al par DataFrame y elimine las filas vacías. Esto construye el primer conjunto de velas, que es igual a la medida recortada de la longitud de retrospección. Luego creamos un spread entre los dos ETF, una unidad de SPY y una unidad de -βi de IWM. Obviamente, este no es un escenario realista, ya que estamos empleando una pequeña cantidad de IWM, lo que no es posible en una implementación práctica.

Por último, creamos el z-score del spread, calculado restando la media del spread y normalizando por la desviación estándar del spread. Es importante señalar que aquí está en juego un “sesgo prospectivo” bastante sutil. Lo dejé en el código intencionalmente porque quería resaltar lo fácil que es cometer errores como este en la investigación. Calcular la media y la desviación estándar de toda la serie temporal de propagación. Si esto pretende reflejar una verdadera exactitud histórica, entonces esta información no se puede obtener porque implícitamente utiliza información del futuro. Por lo tanto, debemos utilizar la media móvil y la desviación estándar para calcular la puntuación z.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

En create_long_short_market_signals, crea señales comerciales. Estos se calculan midiendo el valor de la puntuación z que excede un umbral. Cuando el valor absoluto de la puntuación z es menor o igual a otro umbral (más pequeño), se da una señal para cerrar la posición.

Para lograr esto, es necesario establecer si la estrategia comercial es de “apertura” o de “cierre” para cada línea K. Long_market y short_market son dos variables definidas para rastrear posiciones largas y cortas. Desafortunadamente, es computacionalmente lento ya que es mucho más simple programarlo de manera iterativa que con un enfoque vectorizado. Si bien un gráfico de velas de 1 minuto requiere aproximadamente 700 000 puntos de datos por archivo CSV, ¡aún es relativamente rápido de calcular en mi vieja computadora de escritorio!

Para iterar sobre un DataFrame de pandas (una operación ciertamente poco común), es necesario utilizar el método iterrows, que proporciona un generador iterable:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

En esta etapa, actualizamos los pares para contener las señales largas y cortas reales, lo que nos permite determinar si necesitamos abrir una posición. Ahora necesitamos crear una cartera para rastrear el valor de mercado de las posiciones. La primera tarea es crear una columna de posiciones que combine señales largas y cortas. Esto contendrá una lista de elementos de (1,0,-1) donde 1 representa una posición larga, 0 representa ninguna posición (que debe estar cerrada) y -1 representa una posición corta. Las columnas sym1 y sym2 representan el valor de mercado de las posiciones SPY e IWM al final de cada vela.

Una vez creados los valores de mercado del ETF, los sumamos para producir el valor de mercado total al final de cada vela. Luego se convierte en un valor de retorno a través del método pct_change de ese objeto. Las líneas de código siguientes limpian las entradas erróneas (elementos NaN e inf) y finalmente calculan la curva de equidad completa.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

La función principal lo une todo. Los archivos CSV intradiarios se encuentran en la ruta datadir. Asegúrese de modificar el siguiente código para que apunte a su directorio específico.

Para determinar qué tan sensible es la estrategia al período retrospectivo, es necesario calcular un rango de métricas de desempeño retrospectivo. Seleccioné el porcentaje de rendimiento total final de la cartera como métrica de rendimiento y el rango retrospectivo.[50,200] con un incremento de 10. Puede ver en el código a continuación que la función anterior está envuelta en un bucle for sobre este rango y los otros umbrales permanecen iguales. La tarea final es crear un gráfico de líneas de retrospecciones versus retornos usando matplotlib:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

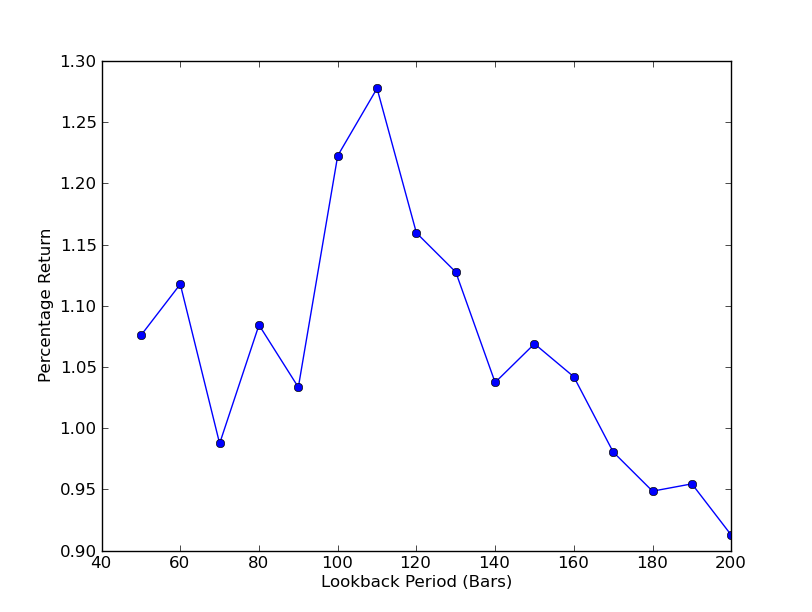
Ahora puedes ver un gráfico de los retornos y las retrospecciones. Tenga en cuenta que hay un máximo “global” para los lookbacks, igual a 110 barras. Si vemos una situación en la que los lookbacks no tienen nada que ver con los retornos es porque:

Análisis de sensibilidad del período retrospectivo de la relación de cobertura de regresión lineal SPY-IWM

¡Ningún artículo sobre backtesting estaría completo sin una curva de ganancias con pendiente ascendente! Entonces, si desea representar gráficamente las ganancias acumuladas en función del tiempo, puede utilizar el siguiente código. Se trazará la cartera final generada a partir del estudio de parámetros retrospectivos. Por lo tanto, es necesario elegir el lookback según el gráfico que desea visualizar. Este gráfico también muestra los rendimientos de SPY durante el mismo período para facilitar la comparación:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

El gráfico de la curva de capital que aparece a continuación tiene un período de retrospección de 100 días:

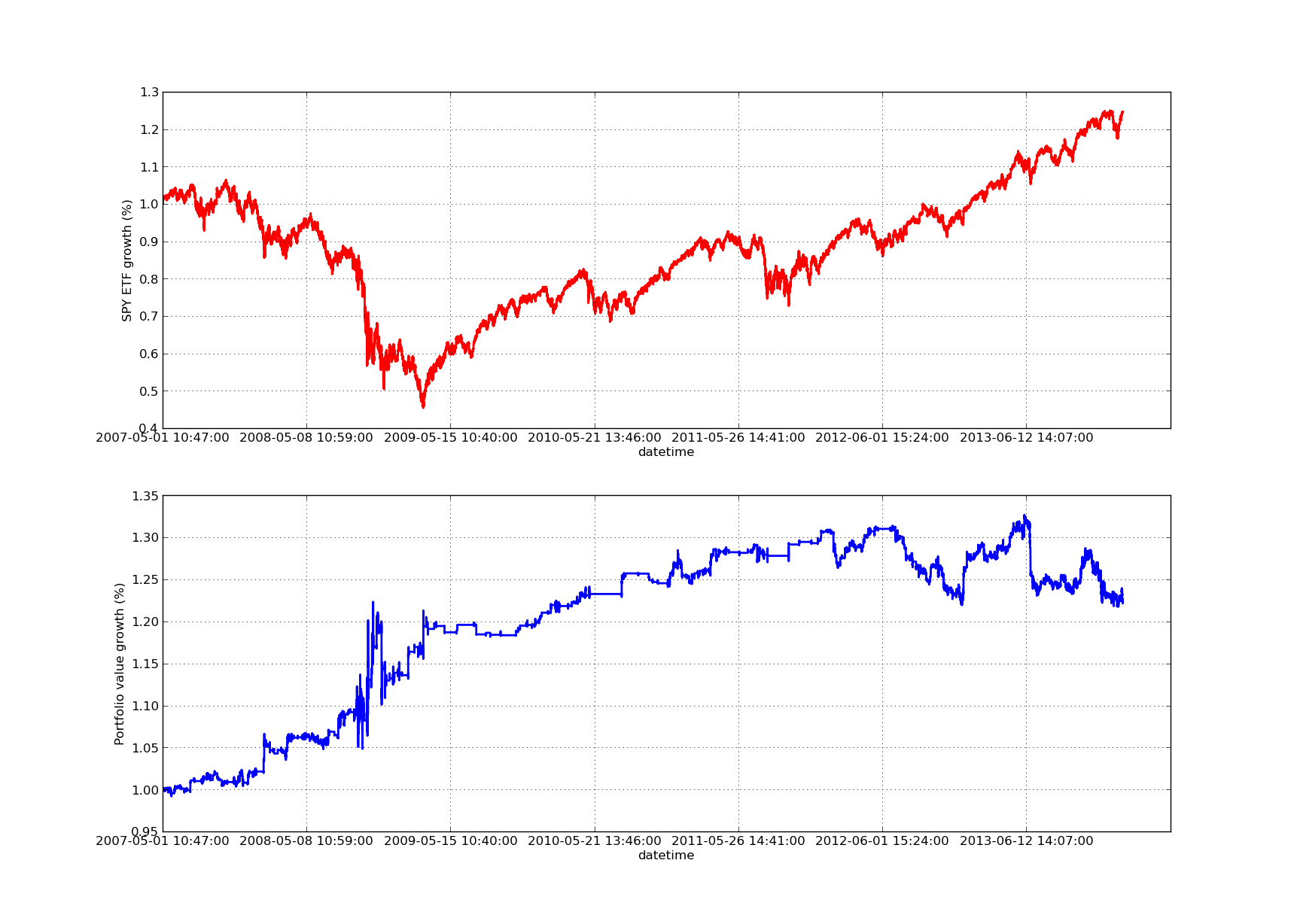
Análisis de sensibilidad del período retrospectivo de la relación de cobertura de regresión lineal SPY-IWM

Cabe señalar que la reducción del SPY fue bastante grande en 2009 durante la crisis financiera. La estrategia también atraviesa un período turbulento durante esta fase. Tenga en cuenta también que el rendimiento se ha deteriorado durante el último año debido a la fuerte tendencia del SPY durante este período, que refleja el S&P 500.

Tenga en cuenta que aún debemos tener en cuenta el “sesgo de anticipación” al calcular el diferencial de puntuación z. Además, todos estos cálculos se realizan sin costes de transacción. Una vez que se tienen en cuenta estos factores, esta estrategia seguramente tendrá malos resultados. Tanto las tarifas como los deslizamientos aún no están determinados. Además, la estrategia se negocia en unidades fraccionarias del ETF, lo que también es muy poco realista.

En un artículo futuro, crearemos un backtester impulsado por eventos más complejo que tendrá en cuenta todo lo anterior, lo que nos dará más confianza en nuestra curva de equidad y en nuestros indicadores de rendimiento.