Déclaration de droit d’auteur: Si vous souhaitez reproduire le code de cet article, veuillez indiquer la source. Si vous utilisez ce code à des fins commerciales, veuillez écrire un article par courrier privé ou contacter l’auteur au [email protected]

1. Introduction

Les avantages de la quantification

Le trading quantitatif est un jugement subjectif basé sur des modèles mathématiques avancés, qui utilise la technologie informatique pour élaborer des stratégies basées sur des données historiques volumineuses, réduisant considérablement l’impact des fluctuations de l’humeur des investisseurs et évitant de prendre des décisions d’investissement irrationnelles dans des conditions de marché extrêmement frénétiques ou pessimistes. La monnaie numérique est devenue une monnaie de plus en plus populaire en Afrique du Sud, en Afrique du Sud et en Afrique du Sud.*La continuité d’un marché de transactions de 7 heures sans interruption et le trading quantitatif peuvent atteindre l’effet de trading à haute fréquence. Il est évident qu’il s’agit d’un bon début pour la quantification.

Le modèle GQNR

Ce modèle est basé sur le modèle de Garch pour prédire les fluctuations, en utilisant la régression non linéaire, par exemple GA, pour prédire le VaR supérieur et le VaR inférieur pour le prochain cycle à l’avenir. Cette méthode est appelée GQNR.

1. Le module Garch

Cette section détaillera la déduction du noyau de la stratégie Garch, qui a une certaine universalité sur les marchés financiers et peut atteindre un certain effet de prédiction sur les monnaies numériques.

Définition de Garch

L’essence du modèle ARCH est d’appliquer la fonction différentielle à la valeur de la fonction différentielle actuelle en déplaçant la planéité de la fonction différentielle en degré q avec une séquence de carré de résidu. Le modèle ARCH ne s’applique en fait qu’aux coefficients de la fonction différentielle à court terme car le modèle de la moyenne mobile a une coupe de degré de la fonction d’auto-corrélation q. Cependant, dans la pratique, certaines fonctions d’écart-différences de séquences de résidu sont auto-dépendantes à long terme, ce qui entraînera des moyennes mobiles élevées, une difficulté accrue d’estimation des paramètres et, finalement, une incidence sur la précision de l’adaptation du modèle ARCH. Afin de corriger ce problème, un modèle de variance conditionnelle de régression générale a été proposé, abrégé GARCH (p,q). Le modèle GARCH est en fait basé sur ARCH, ajoutant la régressivité d’une fonction différentielle de classe p qui prend en compte la fonction différentielle, qui peut être efficacement adaptée à une fonction différentielle avec une mémoire à long terme. Le modèle ARCH est un exemple particulier du modèle GARCH, le modèle GARCH de p = 0 (p,q).

1.2 Le processus ARCH

Si σn est la volatilité estimée de l’actif sur n cycles de négociation au cours de n-1 cycles de négociation, et mu est le rendement journalier, alors on peut faire une estimation sans partialité sur la base du rendement des m derniers cycles de négociation: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\( Les variations suivantes sont effectuées: 1 transforme μn-i en taux de rendement en pourcentage; 2 transforme m-1 en m; 3 suppose que μ = 0 et que ces variations n'affectent pas grand-chose le résultat. Selon la formule ci-dessus, le taux de fluctuation peut être simplifié comme suit: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         C'est-à-dire que le carré de la fluctuation de chaque période a un poids égal à 1/m. Comme il s'agit d'estimer la fluctuation actuelle, les données les plus proches devraient être attribuées un poids plus élevé. \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$ αi est le coefficient de la rentabilité au carré du cycle de transactions i, plus i est positif et plus i est petit, plus la somme des pondérations est 1. Pour une extension plus large, supposons qu’il existe un écart de long terme VL, et que la pondération correspondante est γ, selon la formule ci-dessus:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

Le formulaire 15 peut être modifié comme suit: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( On obtient le procédé ARCH communément appelé \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 Le procédé GARCH

Le modèle GARCH (p,q) est une combinaison des modèles ARCH (p) et EWMA (q), ce qui signifie que la volatilité est liée non seulement aux gains de la période précédente p, mais aussi à la période précédente q elle-même, exprimée comme suit: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\( On obtient la formule suivante: \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 modules QR

Cette section explique la régression décimale fondamentale et décrit l’importance des décimales stratégiques.

Définition du QR

La régression décimale est une méthode de modélisation qui permet d’estimer la relation linéaire entre un ensemble de variables de régression X et les décimales de la variable à interpréter Y. Les modèles de régression antérieurs étaient en fait des attentes conditionnelles des variables à expliquer. On s’intéressait aussi à la relation entre la variable à expliquer et la médiane de la distribution de la variable à expliquer. Elle a été proposée pour la première fois par Koenker et Bassett en 1978.

2.2 De l’OLS au QR

La méthode de régression générale est la méthode du plus petit carré, c’est-à-dire la somme du carré de l’erreur de minimisation: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\( L'objectif de la fraction est de minimiser les valeurs absolues d'erreur pondérée sur la base de la formule ci-dessus et: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

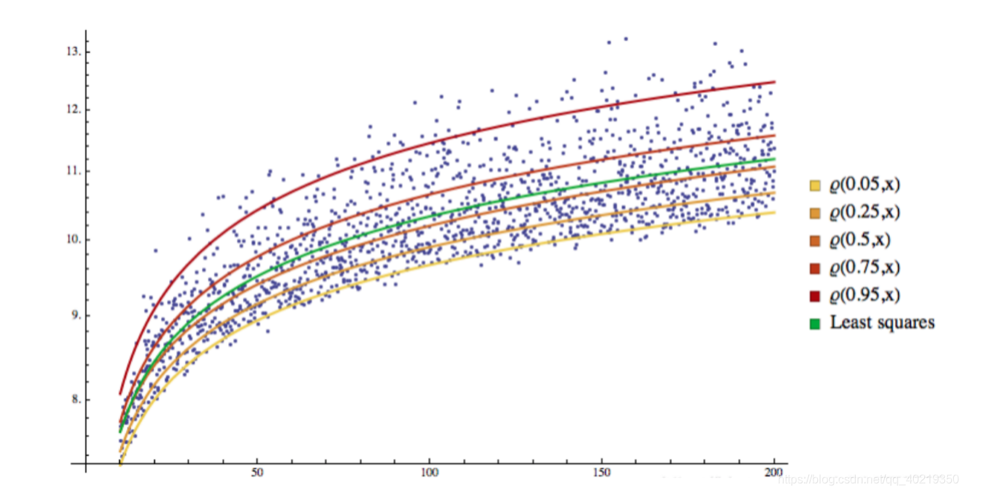
2.2 Visualisation du QR

Vous pouvez voir que tous les échantillons ont été divisés en différents espaces par des lignes de régression, qui deviennent des lignes de partition.

3. Retour à GARCH-QR

Nous nous sommes naturellement demandé si nous pouvions faire une régression de la sigma de la volatilité inconnue du marché avec la fraction Q, VaR, pour prédire la probabilité que la valeur de la marge de fluctuation se déplace dans le futur.

3.1 Sélection du taux de volatilité par rapport à la forme de régression de VaR

Je ne suis pas d’accord avec le fait qu’il y ait une différence entre les deux, mais il y a une différence entre le fait d’avoir une stratégie et de ne pas avoir une stratégie. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Définition de la fonction cible

En combinant les informations ci-dessus, on obtient une fonction cible à optimiser: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Optimisation de la fonction cible par l’apprentissage automatique

Cette étape est plus facultative, la gradience traditionnelle est réduite, mais il est aussi possible d’utiliser des algorithmes génétiques, permettant au lecteur d’expérimenter avec sa propre créativité.Il y a quelque chose à propos de l’algorithme GA

Comment utiliser le GQNR dans la quantification

1. La définition de l’idée

        Le cœur du GQNR réside dans la volatilité du marché, à chaque moment de la période actuelle, on peut prévoir les prévisions de la volatilité de la prochaine période par le biais de GARCH, et d’autre part, on peut obtenir des retours décimaux de la volatilité par le biais de prévisions de données passées.

2. Les difficultés d’utilisation

• Une forme de régression
• Le choix de l’algorithme adaptatif
• Les paramètres appropriés pour l’apprentissage automatique
• L’incertitude et le hasard du marché

3. La solution

• Réduire les cycles d’apprentissage des stratégies
• Réduire le risque à long terme sur une seule garantie de dépôt
• Augmentation de la co-vérification de la tendance à la biconvergence et confirmation de la deuxième dépréciation