इस लेख में, हम एक दिन व्यापार रणनीति लिखेंगे। इसमें “मीन रिवर्सन ट्रेडिंग पेयर्स” की क्लासिक ट्रेडिंग अवधारणा का उपयोग किया जाएगा। इस उदाहरण में, हम दो एक्सचेंज-ट्रेडेड फंड (ETF), SPY और IWM का उपयोग करेंगे, जो न्यूयॉर्क स्टॉक एक्सचेंज (NYSE) पर कारोबार करते हैं और अमेरिकी शेयर बाजार सूचकांक, S&P 500 और रसेल 2000 का प्रतिनिधित्व करने का प्रयास करते हैं।” .

यह रणनीति एक ETF में लंबी अवधि के लिए तथा दूसरे में छोटी अवधि के लिए निवेश करके “कैरी” बनाती है। दीर्घ-लघु अनुपात को कई तरीकों से परिभाषित किया जा सकता है, उदाहरण के लिए सांख्यिकीय सह-एकीकरण समय श्रृंखला विधियों का उपयोग करके। इस परिदृश्य में, हम रोलिंग लीनियर रिग्रेशन के माध्यम से SPY और IWM के बीच हेज अनुपात की गणना करेंगे। इससे हम SPY और IWM के बीच एक “स्प्रेड” बना सकेंगे, जिसे z-स्कोर के लिए सामान्यीकृत किया जाएगा। जब z-स्कोर एक निश्चित सीमा से अधिक हो जाता है, तो एक व्यापार संकेत उत्पन्न होता है, क्योंकि हमारा मानना ​​है कि यह “प्रसार” औसत पर वापस आ जाएगा।

इस रणनीति का तर्क यह है कि SPY और IWM दोनों ही मोटे तौर पर एक ही बाजार परिदृश्य का प्रतिनिधित्व करते हैं, अर्थात बड़ी और छोटी अमेरिकी कंपनियों के समूह के स्टॉक मूल्य का प्रदर्शन। आधार यह है कि यदि आप कीमतों के “औसत प्रत्यावर्तन” सिद्धांत को स्वीकार करते हैं, तो यह हमेशा प्रत्यावर्तन करेगा, क्योंकि “घटनाएं” बहुत ही कम समय में एसएंडपी 500 और रसेल 2000 को अलग-अलग प्रभावित कर सकती हैं, लेकिन उनके बीच “ब्याज दर अंतर” वे हमेशा सामान्य माध्य पर वापस आ जाएंगे, और दोनों की दीर्घकालिक मूल्य श्रृंखला हमेशा सह-एकीकृत होगी।

रणनीति

रणनीति इस प्रकार क्रियान्वित की जाती है:

डेटा - अप्रैल 2007 से फरवरी 2014 तक SPY और IWM के 1-मिनट के कैंडलस्टिक चार्ट प्राप्त करें।

प्रसंस्करण - डेटा को सही ढंग से संरेखित करें और एक दूसरे से गायब पट्टियों को हटा दें। (यदि एक पक्ष गायब है, तो दोनों पक्ष हटा दिए जाएंगे)

स्प्रेड - दो ईटीएफ के बीच हेज अनुपात की गणना रोलिंग लीनियर रिग्रेशन का उपयोग करके की जाती है। लुकबैक विंडो का उपयोग करके बीटा प्रतिगमन गुणांक के रूप में परिभाषित किया गया है जिसे 1 बार आगे बढ़ाया जाता है और प्रतिगमन गुणांक की पुनर्गणना की जाती है। इसलिए, हेजिंग अनुपात βi, bi K-लाइन का उपयोग bi-1-k से bi-1 तक क्रॉसिंग बिंदु की गणना करके K-लाइन का पता लगाने के लिए किया जाता है।

जेड-स्कोर - मानक स्प्रेड का मूल्य सामान्य तरीके से गणना किया जाता है। इसका अर्थ है प्रसार (नमूना) के माध्य को घटाना और प्रसार (नमूना) के मानक विचलन से विभाजित करना। ऐसा करने का कारण यह है कि थ्रेशोल्ड पैरामीटर को समझना आसान हो जाए, क्योंकि Z-स्कोर एक आयामहीन मात्रा है। मैंने जानबूझकर गणनाओं में “पूर्वानुमान पूर्वाग्रह” को शामिल किया, ताकि यह दिखाया जा सके कि यह कितना सूक्ष्म हो सकता है। इसे आज़माइए!

ट्रेडिंग - जब नकारात्मक z-स्कोर मान पूर्व निर्धारित (या पोस्ट-अनुकूलित) सीमा से नीचे चला जाता है, तो दीर्घ संकेत उत्पन्न होते हैं, जबकि लघु संकेत इसके विपरीत तरीके से उत्पन्न होते हैं। जब z-स्कोर का निरपेक्ष मान एक अतिरिक्त सीमा से नीचे चला जाता है, तो स्थिति को बंद करने का संकेत उत्पन्न होता है। इस रणनीति के लिए, मैंने (कुछ हद तक मनमाने ढंग से) प्रवेश सीमा के रूप में |z| = 2 और निकास सीमा के रूप में |z| = 1 चुना। यह मानते हुए कि प्रसार में माध्य प्रत्यावर्तन की भूमिका होती है, उम्मीद है कि उपरोक्त उपाय इस अंतरपणन संबंध को पकड़ लेगा और अच्छा लाभ प्रदान करेगा।

किसी रणनीति को गहराई से समझने का शायद सबसे अच्छा तरीका उसे वास्तव में क्रियान्वित करना है। निम्नलिखित अनुभाग में इस माध्य प्रत्यावर्तन रणनीति को क्रियान्वित करने के लिए प्रयुक्त सम्पूर्ण पायथन कोड (एकल फ़ाइल) का विवरण दिया गया है। मैंने आपको बेहतर समझने में मदद करने के लिए विस्तृत कोड टिप्पणियाँ जोड़ी हैं।

पायथन कार्यान्वयन

सभी पायथन/पांडा ट्यूटोरियल्स की तरह, आपका पायथन वातावरण इस ट्यूटोरियल में बताए अनुसार सेट किया जाना चाहिए। एक बार सेटअप पूरा हो जाने पर, पहला कार्य आवश्यक पायथन लाइब्रेरीज़ को आयात करना है। यह matplotlib और pandas का उपयोग करने के लिए आवश्यक है।

मैं जिन विशिष्ट लाइब्रेरी संस्करणों का उपयोग कर रहा हूं वे इस प्रकार हैं:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

आइये आगे बढ़ें और इन लाइब्रेरीज़ को आयात करें:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

निम्नलिखित फ़ंक्शन create_pairs_dataframe दो प्रतीकों के इंट्राडे कैंडलस्टिक्स युक्त दो CSV फ़ाइलों को आयात करता है। हमारे मामले में, यह SPY और IWM होगा। इसके बाद यह एक अलग “डेटा फ्रेम की जोड़ी” बनाता है जो दोनों मूल फाइलों के इंडेक्स का उपयोग करता है। छूटे हुए लेन-देन और त्रुटियों के कारण उनके टाइमस्टैम्प भिन्न हो सकते हैं। यह पांडा जैसी डेटा विश्लेषण लाइब्रेरी का उपयोग करने के मुख्य लाभों में से एक है। हम “बॉयलरप्लेट” कोड को बहुत कुशल तरीके से संभालते हैं।

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

अगला चरण SPY और IWM के बीच रोलिंग रैखिक प्रतिगमन करना है। इस परिदृश्य में, IWM पूर्वानुमानक (‘x’) है और SPY प्रतिक्रिया (‘y’) है। मैंने 100 कैंडलस्टिक्स की एक डिफ़ॉल्ट लुकबैक विंडो सेट की है। जैसा कि ऊपर बताया गया है, ये रणनीति के पैरामीटर हैं। किसी रणनीति को मजबूत माने जाने के लिए, हम आदर्श रूप से एक रिटर्न रिपोर्ट देखना चाहेंगे जो लुकबैक अवधि (या कुछ अन्य प्रदर्शन माप) पर उत्तल हो। इसलिए, कोड के बाद के चरण में, हम दायरे के भीतर लुक-बैक अवधि को बदलकर संवेदनशीलता विश्लेषण करेंगे।

SPY-IWM के लिए रैखिक प्रतिगमन मॉडल में रोलिंग बीटा गुणांक की गणना करने के बाद, इसे डेटाफ़्रेम जोड़ी में जोड़ें और खाली पंक्तियों को हटा दें। इससे कैंडलस्टिक्स का पहला सेट निर्मित होता है, जो लुकबैक लम्बाई के ट्रिम किए गए माप के बराबर होता है। इसके बाद हमने दो ETF के बीच एक स्प्रेड बनाया, SPY की एक इकाई और IWM की -βi की एक इकाई। जाहिर है, यह यथार्थवादी परिदृश्य नहीं है, क्योंकि हम IWM की एक छोटी मात्रा का उपयोग कर रहे हैं, जो व्यावहारिक कार्यान्वयन में संभव नहीं है।

अंत में, हम स्प्रेड का z-स्कोर बनाते हैं, जिसकी गणना स्प्रेड के माध्य को घटाकर और स्प्रेड के मानक विचलन द्वारा सामान्यीकृत करके की जाती है। यह ध्यान रखना महत्वपूर्ण है कि यहां एक सूक्ष्म “भविष्य-उन्मुख पूर्वाग्रह” काम कर रहा है। मैंने इसे जानबूझकर कोड में छोड़ दिया क्योंकि मैं यह बताना चाहता था कि शोध में इस तरह की गलतियाँ करना कितना आसान है। संपूर्ण प्रसार समय श्रृंखला के माध्य और मानक विचलन की गणना करें। यदि इसका उद्देश्य सच्ची ऐतिहासिक सटीकता को प्रतिबिंबित करना है, तो यह जानकारी प्राप्त नहीं की जा सकती, क्योंकि यह भविष्य की जानकारी का उपयोग करती है। इसलिए, हमें z-स्कोर की गणना करने के लिए रोलिंग माध्य और stdev का उपयोग करना चाहिए।

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

create_long_short_market_signals में, ट्रेडिंग सिग्नल बनाएं। इनकी गणना एक सीमा से अधिक z-स्कोर मान को मापकर की जाती है। जब z-स्कोर का निरपेक्ष मान किसी अन्य (छोटी) सीमा से कम या बराबर होता है, तो स्थिति को बंद करने का संकेत दिया जाता है।

इसे प्राप्त करने के लिए, यह स्थापित करना आवश्यक है कि क्या ट्रेडिंग रणनीति प्रत्येक K-लाइन के लिए “ओपनिंग” या “क्लोजिंग” है। लॉन्ग_मार्केट और शॉर्ट_मार्केट दो चर हैं जिन्हें लॉन्ग और शॉर्ट पोजीशन को ट्रैक करने के लिए परिभाषित किया गया है। दुर्भाग्यवश, यह कम्प्यूटेशनल रूप से धीमा है, क्योंकि वेक्टराइज्ड दृष्टिकोण की तुलना में पुनरावृत्तीय तरीके से प्रोग्राम करना अधिक सरल है। हालांकि 1 मिनट के कैंडलस्टिक चार्ट के लिए प्रति CSV फ़ाइल ~700,000 डेटा बिंदुओं की आवश्यकता होती है, फिर भी मेरे पुराने डेस्कटॉप पर इसकी गणना करना अपेक्षाकृत तेज़ है!

पांडा डेटाफ्रेम (जो एक असामान्य ऑपरेशन है) पर पुनरावृति करने के लिए, iterrows विधि का उपयोग करना आवश्यक है, जो एक पुनरावृत्त जनरेटर प्रदान करता है:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

इस स्तर पर, हम वास्तविक लंबे और छोटे संकेतों को शामिल करने के लिए जोड़ों को अपडेट करते हैं, जो हमें यह निर्धारित करने की अनुमति देता है कि हमें कोई स्थिति खोलने की आवश्यकता है या नहीं। अब हमें पोजीशन के बाजार मूल्य पर नज़र रखने के लिए एक पोर्टफोलियो बनाने की ज़रूरत है। पहला कार्य एक स्थिति स्तंभ बनाना है जो लंबे और छोटे संकेतों को जोड़ता है। इसमें (1,0,-1) से तत्वों की एक सूची होगी, जहां 1 लंबी स्थिति को दर्शाता है, 0 कोई स्थिति नहीं दर्शाता है (जिसे बंद किया जाना चाहिए), और -1 छोटी स्थिति को दर्शाता है। sym1 और sym2 कॉलम प्रत्येक कैंडलस्टिक के अंत में SPY और IWM स्थितियों के बाजार मूल्य को दर्शाते हैं।

एक बार जब ईटीएफ बाजार मूल्य तैयार हो जाते हैं, तो हम उन्हें प्रत्येक कैंडलस्टिक के अंत में कुल बाजार मूल्य बनाने के लिए जोड़ते हैं। फिर इसे उस ऑब्जेक्ट की pct_change विधि के माध्यम से रिटर्न मान में परिवर्तित कर दिया जाता है। कोड की आगामी पंक्तियाँ गलत प्रविष्टियों (NaN और inf तत्व) को साफ़ करती हैं और अंत में सम्पूर्ण इक्विटी वक्र की गणना करती हैं।

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

मुख्य कार्य यह सब एक साथ जोड़ता है। इंट्राडे CSV फ़ाइलें datadir पथ में स्थित हैं। कृपया निम्नलिखित कोड को अपनी विशिष्ट निर्देशिका की ओर इंगित करने के लिए संशोधित करना सुनिश्चित करें।

यह निर्धारित करने के लिए कि रणनीति लुकबैक अवधि के प्रति कितनी संवेदनशील है, लुकबैक प्रदर्शन मेट्रिक्स की एक श्रृंखला की गणना करना आवश्यक है। मैंने प्रदर्शन मीट्रिक और लुकबैक रेंज के रूप में पोर्टफोलियो के अंतिम कुल रिटर्न प्रतिशत का चयन किया।[50,200] को 10 की वृद्धि के साथ। आप नीचे दिए गए कोड में देख सकते हैं कि पिछला फ़ंक्शन इस सीमा पर एक फ़ॉर लूप में लपेटा गया है और अन्य सीमाएँ समान हैं। अंतिम कार्य matplotlib का उपयोग करके लुकबैक बनाम रिटर्न का एक लाइन चार्ट बनाना है:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

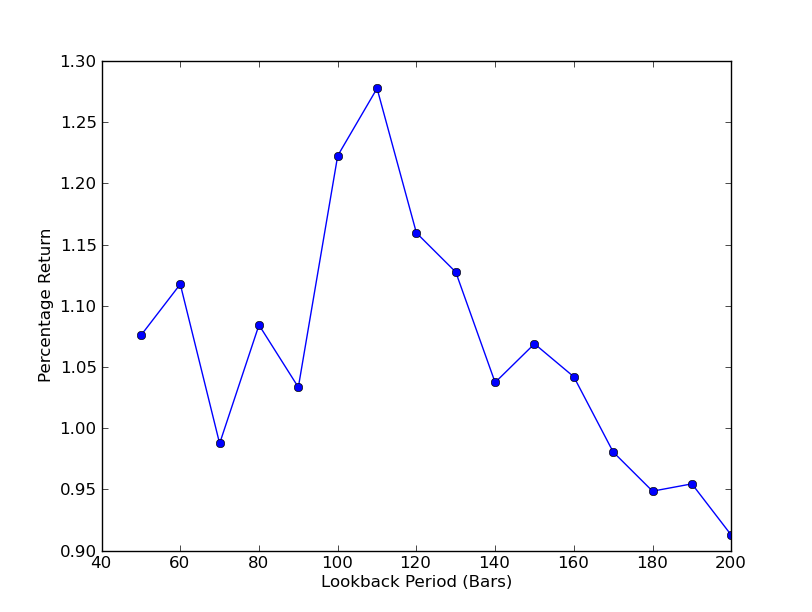
अब आप लुकबैक और रिटर्न का ग्राफ देख सकते हैं। ध्यान दें कि लुकबैक के लिए एक “वैश्विक” अधिकतम सीमा है, जो 110 बार के बराबर है। यदि हम ऐसी स्थिति देखते हैं जहां लुकबैक का रिटर्न से कोई संबंध नहीं है, तो इसका कारण यह है:

SPY-IWM रैखिक प्रतिगमन हेज अनुपात लुकबैक अवधि संवेदनशीलता विश्लेषण

कोई भी बैकटेस्टिंग लेख ऊपर की ओर झुके हुए लाभ वक्र के बिना पूरा नहीं होगा! इसलिए यदि आप समय के अनुसार संचयी लाभ रिटर्न का आरेख बनाना चाहते हैं, तो आप निम्नलिखित कोड का उपयोग कर सकते हैं। यह लुकबैक पैरामीटर अध्ययन से उत्पन्न अंतिम पोर्टफोलियो का खाका तैयार करेगा। इसलिए, यह आवश्यक है कि आप उस चार्ट के अनुसार लुकबैक चुनें जिसे आप देखना चाहते हैं। तुलना में सहायता के लिए यह चार्ट उसी अवधि में SPY के रिटर्न को भी दर्शाता है:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

नीचे दिए गए इक्विटी वक्र चार्ट में 100 दिनों की लुकबैक अवधि है:

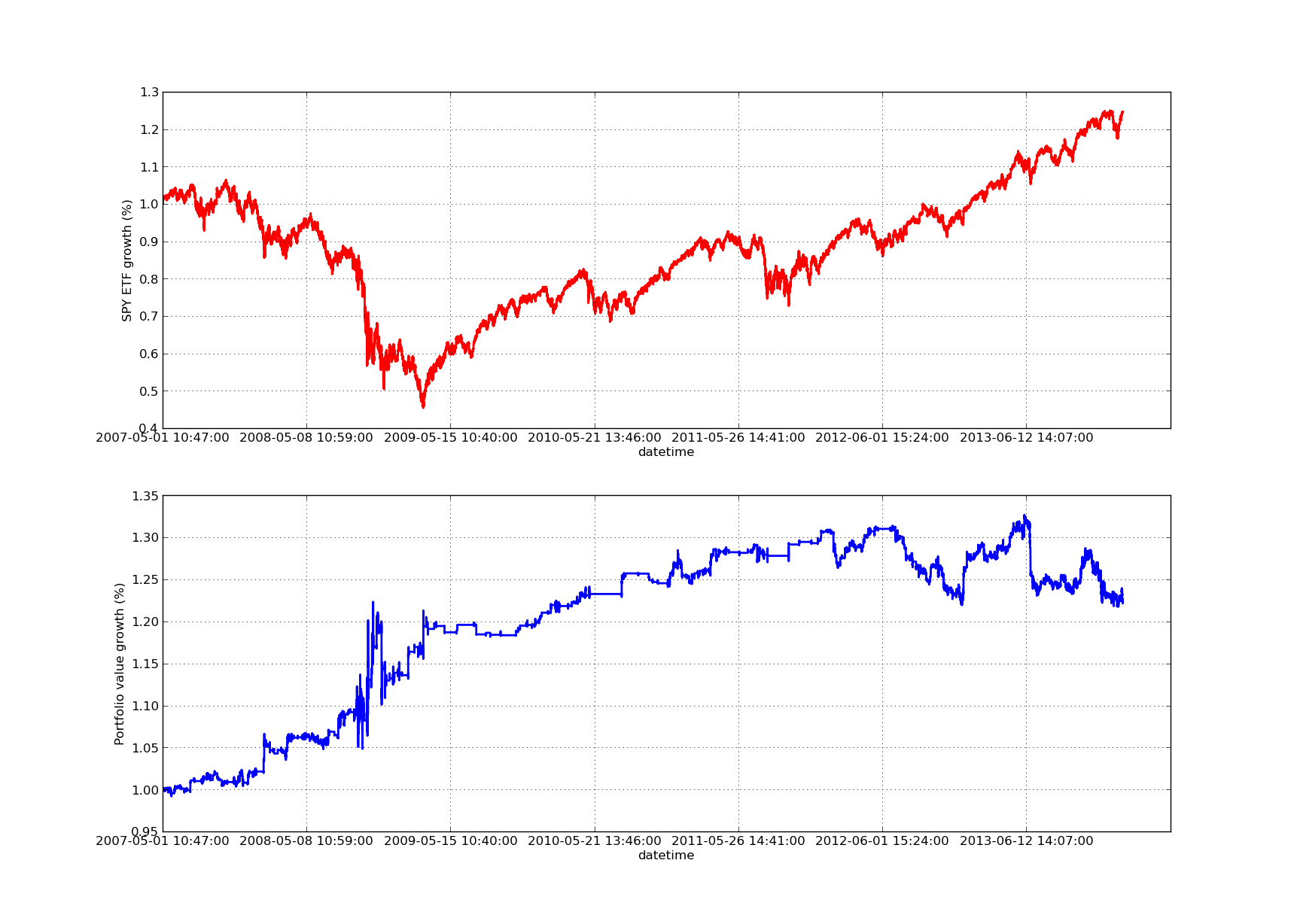
SPY-IWM रैखिक प्रतिगमन हेज अनुपात लुकबैक अवधि संवेदनशीलता विश्लेषण

ध्यान दें कि 2009 में वित्तीय संकट के दौरान SPY में गिरावट काफी बड़ी थी। इस चरण के दौरान रणनीति भी उथल-पुथल भरी अवधि में है। यह भी ध्यान दें कि पिछले वर्ष की तुलना में प्रदर्शन में गिरावट आई है, क्योंकि इस अवधि के दौरान एस.एण्ड.पी. 500 के समान एस.पी.वाई. की प्रवृत्ति मजबूत रही।

ध्यान दें कि z-स्कोर प्रसार की गणना करते समय हमें अभी भी “लुकअहेड पूर्वाग्रह” को ध्यान में रखना होगा। इसके अलावा, ये सभी गणनाएं लेनदेन लागत के बिना की जाती हैं। एक बार इन कारकों को ध्यान में रख लिया जाए तो यह रणनीति खराब प्रदर्शन करेगी। शुल्क और स्लिपेज दोनों फिलहाल अनिर्धारित हैं। इसके अतिरिक्त, यह रणनीति ईटीएफ की आंशिक इकाइयों में व्यापार करती है, जो अत्यधिक अवास्तविक है।

आगामी लेख में, हम एक अधिक जटिल घटना-संचालित बैकटेस्टर बनाएंगे जो उपरोक्त सभी बातों को ध्यान में रखेगा, जिससे हमें अपने इक्विटी वक्र और प्रदर्शन संकेतकों में अधिक विश्वास प्राप्त होगा।