Catatan: Kasus ini hanya digunakan untuk tujuan studi dan penelitian, bukan sebagai rekomendasi investasi.

Data harga Bitcoin didasarkan pada urutan waktu, sehingga harga Bitcoin diprediksi menggunakan model LSTM.

Memori jangka pendek jangka panjang (LSTM) adalah model pembelajaran mendalam yang sangat cocok untuk data berurutan waktu (atau data dengan urutan waktu / spasial / struktural, seperti film, kalimat, dll.), Model ini ideal untuk memprediksi arah harga cryptocurrency.

Artikel ini ditulis terutama untuk memprediksi harga Bitcoin di masa depan melalui data yang disesuaikan dengan LSTM.

Perpustakaan yang dibutuhkan untuk import

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Analisis data

Pengungkapan data

Baca data perdagangan harian BTC

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Untuk melihat data yang tersedia, sekarang ada 1380 data yang terdiri dari kolom Date, Open, High, Low, Close, Volume (BTC), Volume (Currency), dan Harga Berat.

data.info()

Lihat 10 baris pertama data di bawah ini.

data.head(10)

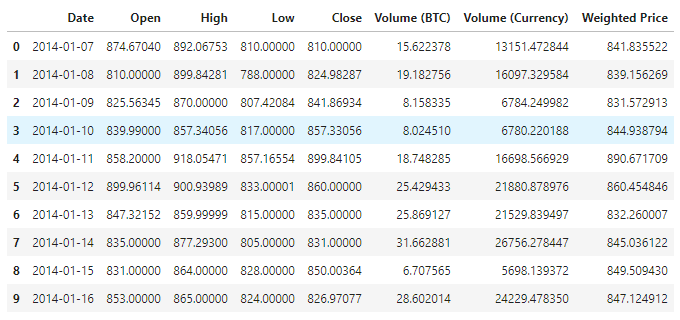
Visualisasi data

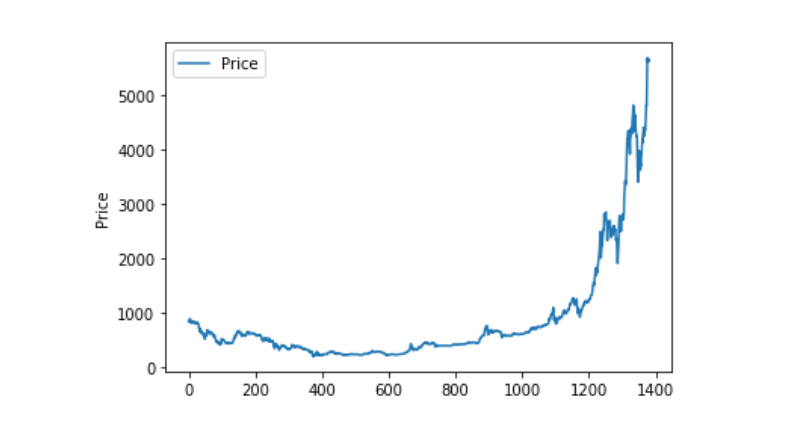
Gunakan matplotlib untuk memetakan harga tertimbang dan melihat bagaimana data tersebut terdistribusi. Di dalam grafik, kita menemukan bagian dengan data 0, dan kita perlu memastikan apakah ada yang tidak normal dalam data tersebut.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Pengolahan data yang tidak normal

Jika kita melihat apakah ada data yang mengandung nan, kita bisa melihat bahwa data yang tidak mengandung nan tidak ada dalam data kita.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Jika kita melihat data nol, kita dapat melihat bahwa data kita memiliki nilai nol, dan kita perlu melakukan sesuatu dengan nilai nol.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

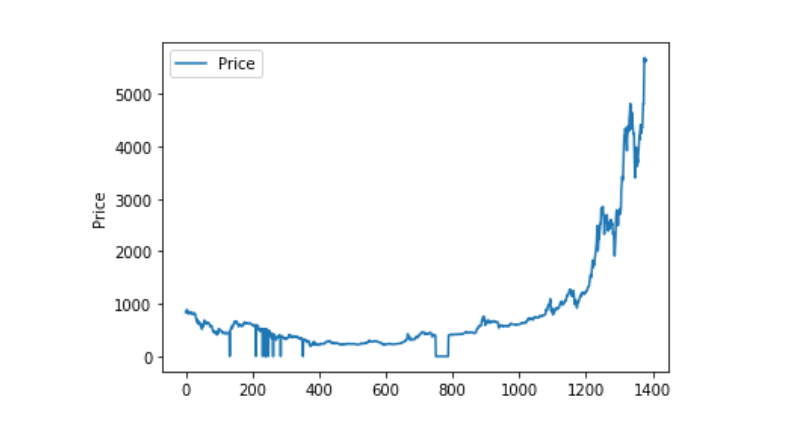
Jika kita melihat distribusi dan pergerakan data, pada titik ini kurva sudah sangat kontinu.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Pemisahan antara Training Dataset dan Test Dataset

Mengintegrasikan data ke 0-1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Pembagian test dataset dan training dataset dengan 2:8

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Untuk membuat dataset pelatihan dan uji coba, gunakan 1 hari sebagai periode jendela untuk membuat dataset pelatihan dan uji coba kami.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Mendefinisikan dan melatih model

Kali ini kita akan menggunakan model sederhana, dan modelnya adalah 1. LSTM2. Dense。

Input Shape memiliki dimensi ((batch_size, time steps, features)). Di sini, nilai time steps adalah interval jendela waktu saat data dimasukkan, di sini kita menggunakan 1 hari sebagai jendela waktu, dan data kita adalah data harian, jadi di sini langkah-langkah waktu kita adalah 1.

Long short-term memory (LSTM) adalah sebuah RNN khusus, terutama untuk mengatasi hilangnya gradien dan ledakan gradien dalam proses pelatihan sekuens panjang.

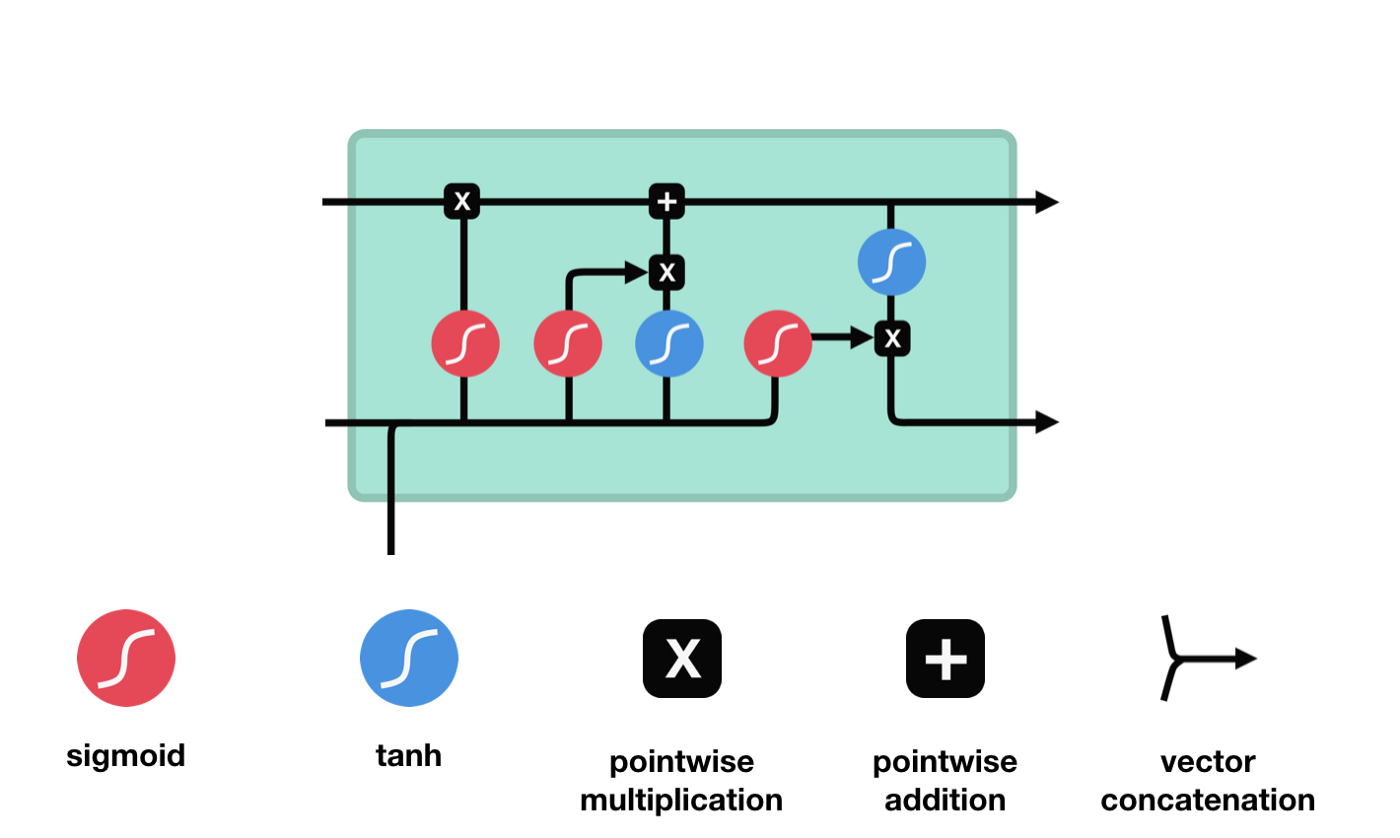
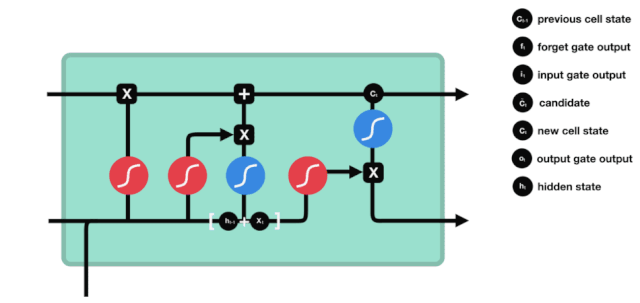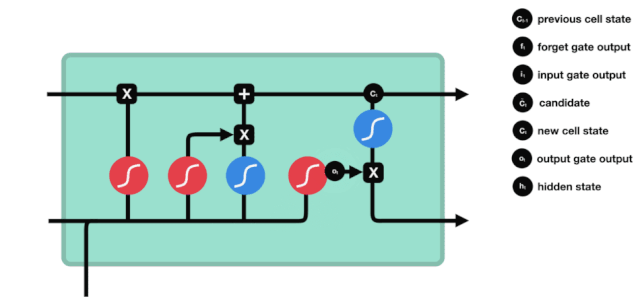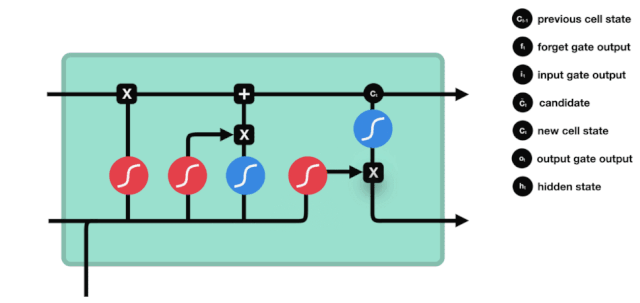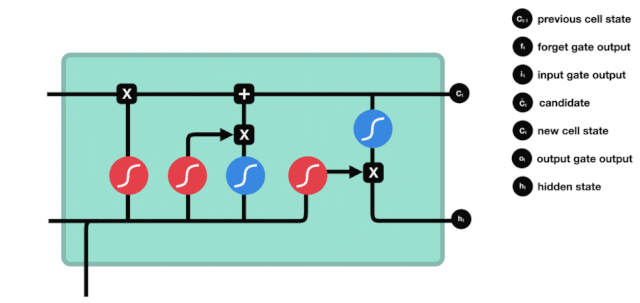
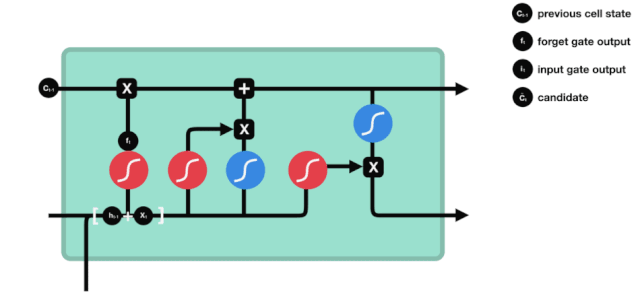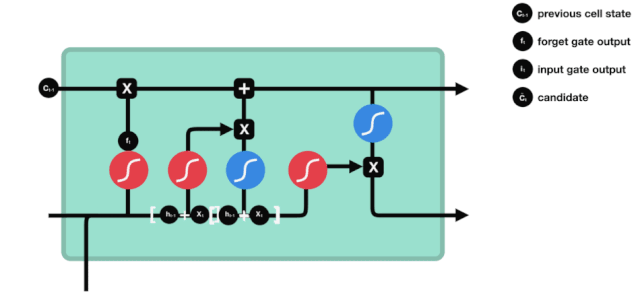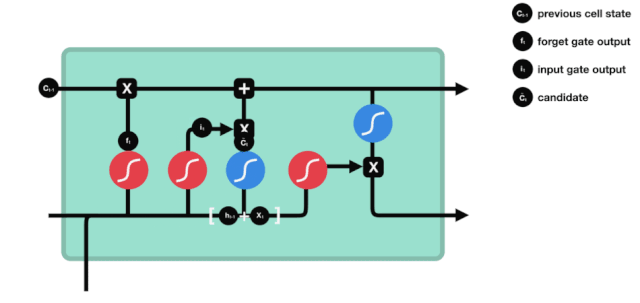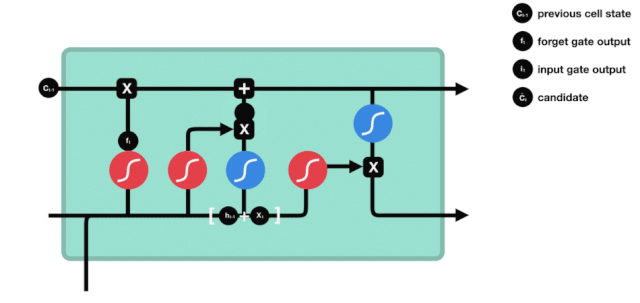
Dari diagram struktur jaringan LSTM, dapat dilihat bahwa LSTM sebenarnya adalah sebuah model kecil yang terdiri dari 3 fungsi aktivasi sigmoid, 2 fungsi aktivasi tanh, 3 fungsi perkalian, dan 1 fungsi penjumlahan.

Status sel

Status sel adalah inti dari LSTM, dia adalah garis hitam di bagian atas dari gambar di atas, di bawah garis hitam ini adalah beberapa pintu, kita akan memaparkan di belakang. Status sel akan diperbarui berdasarkan hasil dari setiap pintu.

Jaringan LSTM dapat menghapus atau menambahkan informasi dari status sel melalui struktur yang disebut pintu. Pintu dapat memiliki keputusan selektif tentang informasi apa yang harus dilalui. Struktur pintu adalah kombinasi dari lapisan sigmoid dan operasi perkalian titik. Karena output dari lapisan sigmoid adalah nilai 0-1, 0 tidak dapat dilalui, 1 dapat dilalui.

Gerbang Kelimpahan

Langkah pertama dari LSTM adalah menentukan informasi apa yang perlu dibuang oleh sel. Bagian dari operasi ini dilakukan oleh sebuah unit sigmoid yang disebut gerbang lupa.

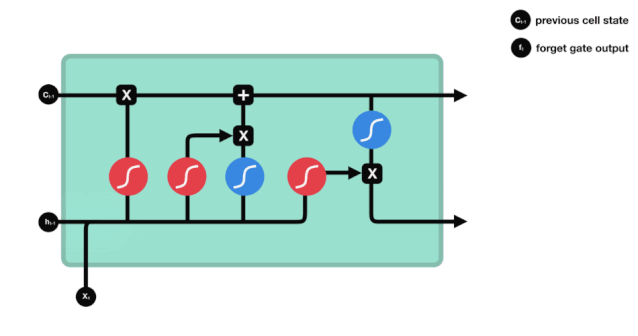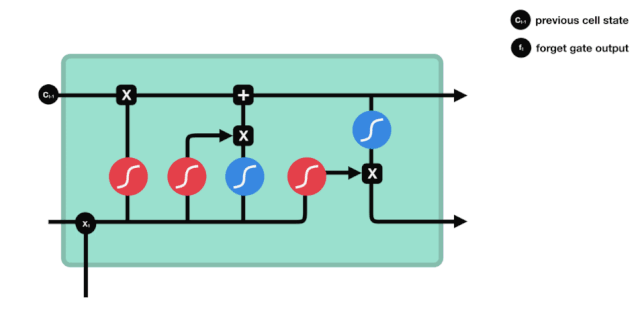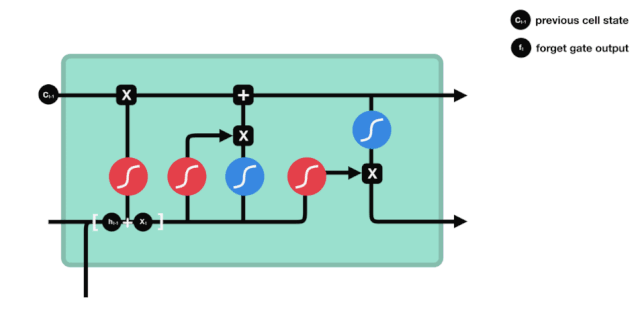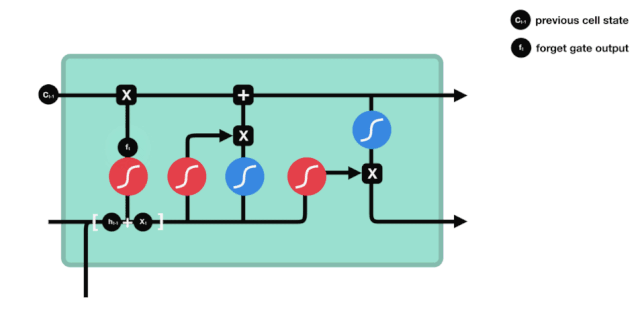
Kita dapat melihat bahwa gerbang pelupa outputkan vektor antara 0-1 dengan melihat informasi \(h_{l-1}\) dan \(x_{t}\), dimana nilai 0-1 dalam vektor tersebut menunjukkan berapa banyak informasi yang disimpan atau dibuang dalam keadaan sel \(C_{t-1}\). 0 berarti tidak disimpan, dan 1 berarti disimpan.

Ekspresi matematis: \(f_{t} =\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

Pintu masuk

Langkah selanjutnya adalah memutuskan informasi baru apa yang akan ditambahkan ke status sel, dan langkah ini dilakukan dengan membuka pintu masuk.

Kita melihat informasi \(h_{l-1}\) dan \(x_{t}\) dimasukkan ke dalam sebuah gerbang lupa (sigmoid) dan gerbang masuk (tanh). Karena output gerbang lupa adalah nilai 0-1, maka, jika gerbang lupa itu 0 maka hasil setelah gerbang masuk \(C_{i}\) tidak akan ditambahkan ke dalam keadaan sel saat ini, jika 1, semuanya akan ditambahkan ke dalam keadaan sel, maka fungsi gerbang lupa di sini adalah untuk menambahkan hasil gerbang masuk secara selektif ke dalam keadaan sel.

Rumus matematika adalah: \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

Pintu keluar

Setelah status sel diperbarui, kita perlu mengevaluasi status sel yang keluar berdasarkan jumlah input \(h_{l-1}\) dan \(x_{t}\). Kita perlu mengevaluasi status sel yang keluar melalui lapisan sigmoid yang disebut output gate, lalu mengevaluasi status sel melalui lapisan tanh untuk mendapatkan vektor dengan nilai antara -1 ~ 1, yang dikalikan dengan nilai output gate untuk mendapatkan output dari unit RNN akhir.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

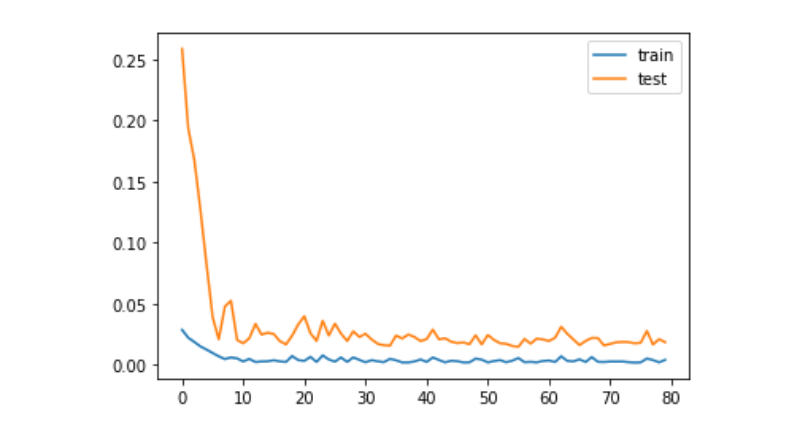
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Prediksi

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

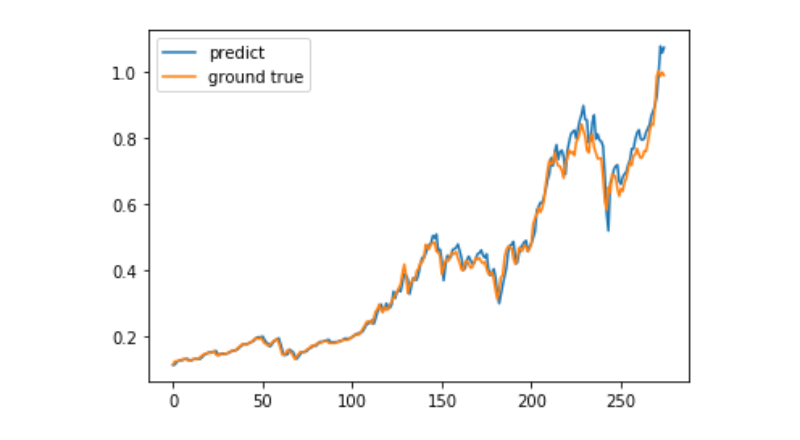
Untuk memprediksi pergerakan harga Bitcoin dalam jangka panjang masih sangat sulit menggunakan pembelajaran mesin, dan artikel ini hanya dapat digunakan sebagai studi kasus.