参考:このケースは,学習・研究目的のみで,投資勧告ではありません.

ビットコインの価格データは時間序列に基づいているため,ビットコインの価格予測はLSTMモデルで実現される.

長期短期記憶 (LSTM) は,タイムシーケンスのデータ (または時間/空間/構造の順序を持つデータ,例えば映画,文など) に特に適した深層学習モデルであり,暗号通貨の価格の動きを予測する理想的なモデルである.

この記事は主にLSTMによるデータマッチングを行い,ビットコインの将来の価格を予測している.

import が使用するライブラリ

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

データ分析

データの読み込み

“BTC”の1日の取引データを読み取ります

data = pd.read_csv(filepath_or_buffer="btc_data_day")

データを表示すると,現在のデータには合計1380個のデータがあり,データはDate,Open,High,Low,Close,Volume (BTC),Volume (Currency),Weighted Priceの列で構成されている.このうちDate列を除いて,残りのデータ列はfloat64データ型である.

data.info()

この10行目のデータを見てください.

data.head(10)

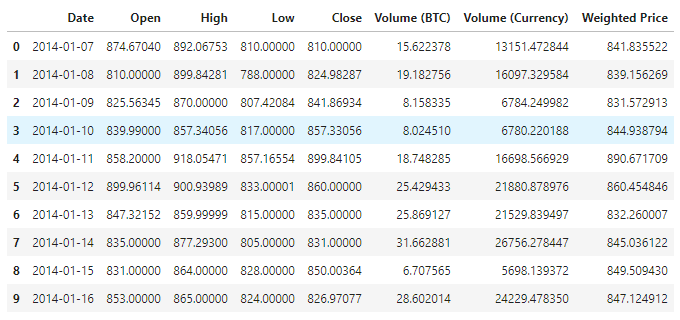
データ可視化

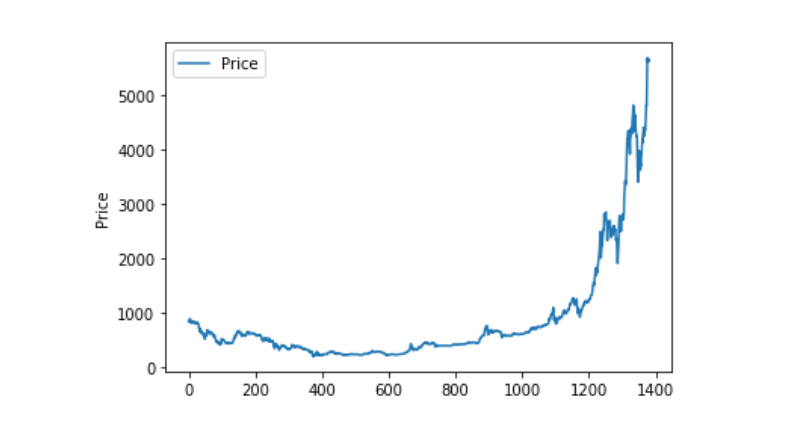
matplotlibを使って,Weighted Priceをマッピングして,データの分布と動きを見てください.図にデータ0がある部分があります.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

異常なデータ処理

データを調べると,nANのデータがないことがわかります.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

0 の値が 0 の値と一致します. 0 の値と一致します.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

この曲線は,非常に連続しています.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

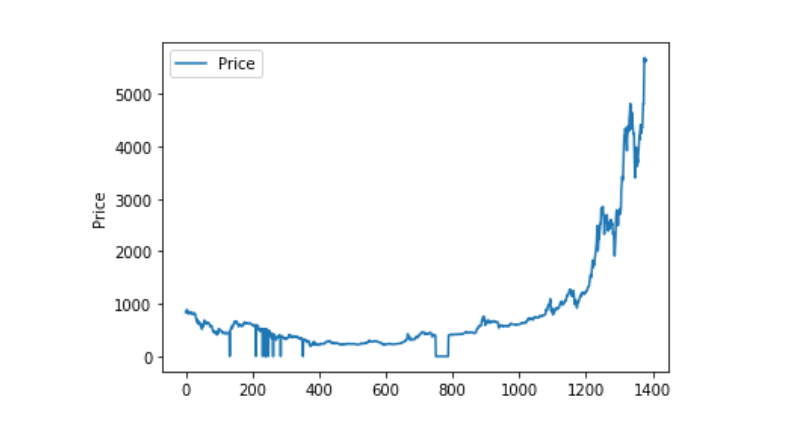
トレーニングデータセットとテストデータセットの分割

データを 0−1 に統一する

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

2:8でテストデータセットとトレーニングデータセットを分割する

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

訓練データセットとテストデータセットを作成し,1日をウィンドウ期間として訓練データセットとテストデータセットを作成します.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

モデルを定義し,訓練する

簡単なモデルで,このモデルには,次の構造があります.. LSTM2. Dense。

ここで,LSTMのinputh shapeについて説明する必要がある.Input Shapeの入力次元は ((batch_size, time steps, features) である.その中で,time stepsはデータ入力時の時間窓の間隔である.ここで,私たちは1日を時間窓として使用し,私たちのデータは日データであり,したがってここでは私たちのtime stepsは1である.

ロングショートタームメモリ (LSTM) は,長シーケンストレーニングにおける梯度消失と梯度爆破の問題を解くための特殊なRNNである.ここでLSTMについて簡単に説明する.

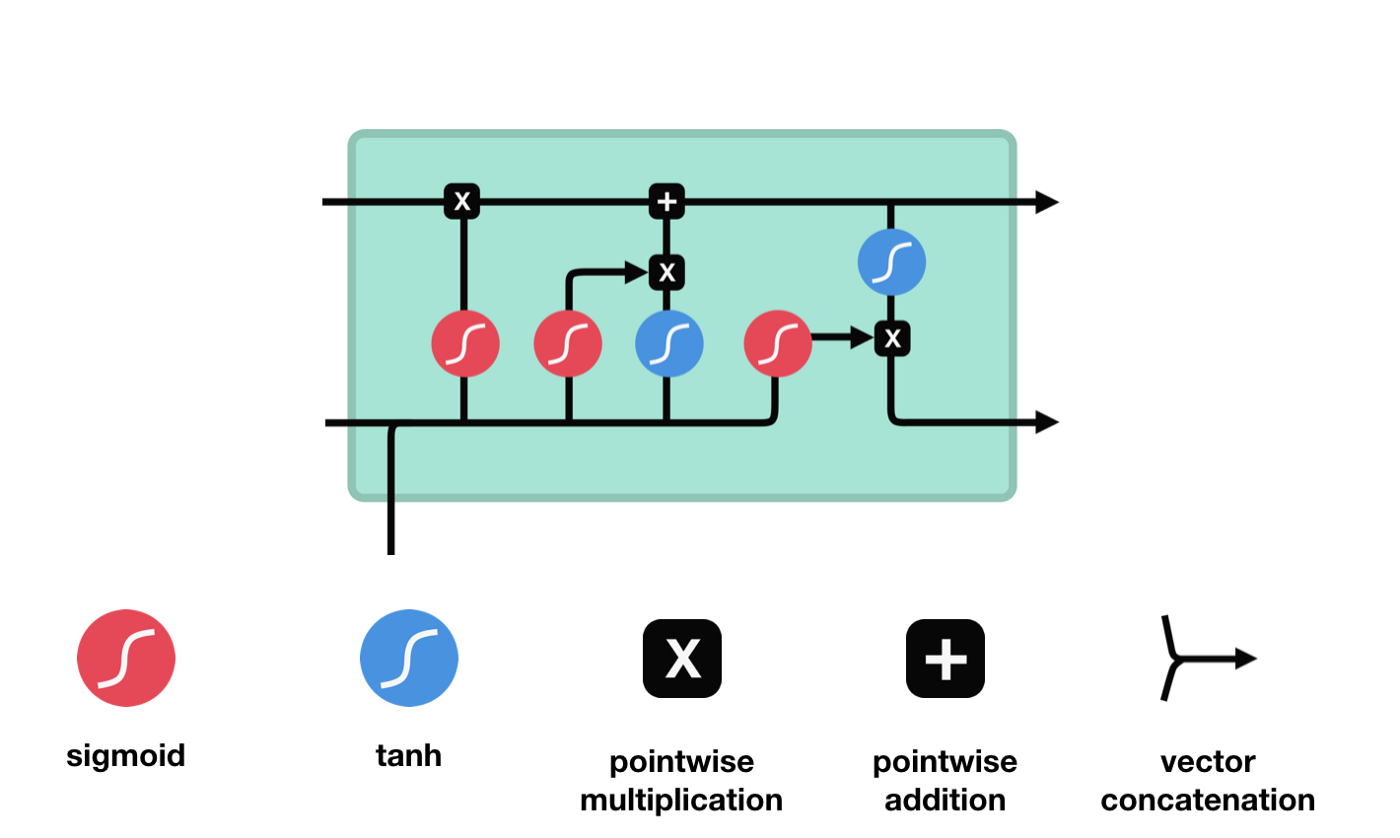
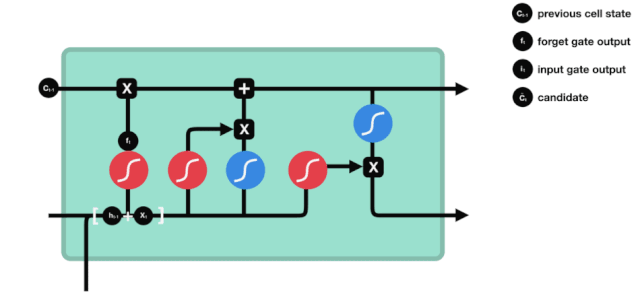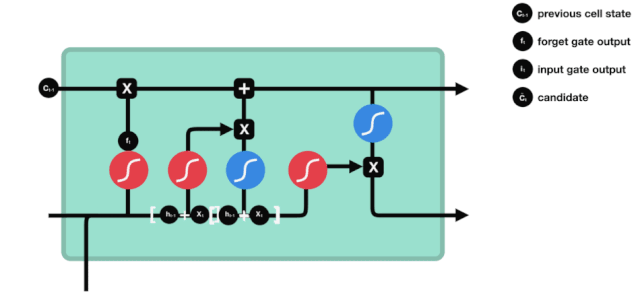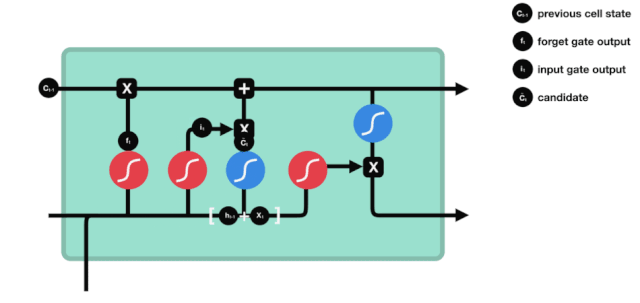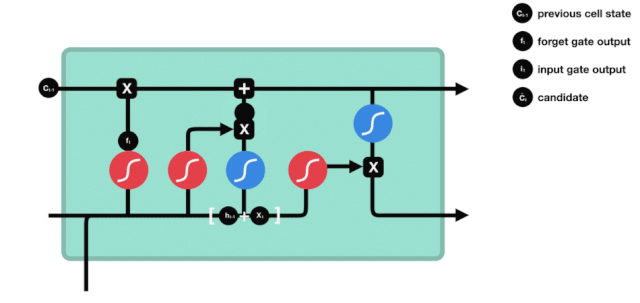
LSTMのネットワーク構造図から,LSTMは実際には3つのシグモイドアクティベーション関数,2つのタンハアクティベーション関数,3つの掛け算,1つの加算を含む小さなモデルであることがわかります.

細胞の状態

細胞状態はLSTMの核心であり,上図の最も上にある黒い線である.この黒い線の下には,いくつかの扉があり,後述する.細胞状態は,各扉の結果に応じて更新される.以下にこれらの扉を紹介すると,細胞状態の流れを理解する.

LSTMネットワークは,ゲートと呼ばれる構造によって細胞状態に情報を削除または追加することができる.ゲートは,どの情報を通過させるかを選択的に決定することができる.ゲートの構造は,シグモイド層と点乗算操作の組み合わせである.シグモイド層の出力は0-1の値であるため,0は通過できない,1は通過することができる.LSTMには,細胞状態を制御する3つのゲートが含まれている.

忘却の扉

LSTMの最初のステップは,細胞状態がどの情報を捨てる必要があるかを決定することです. この操作は,忘却門と呼ばれるシグモイド単位によって処理されます. アニメーション図を見てみましょう.

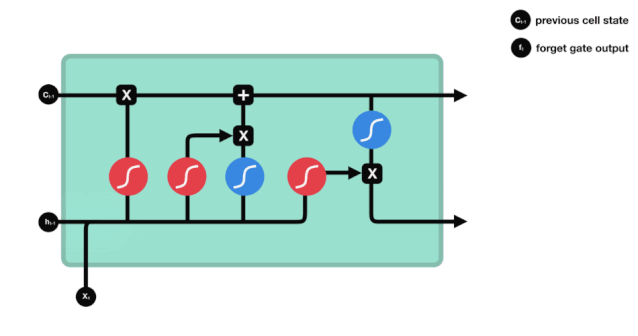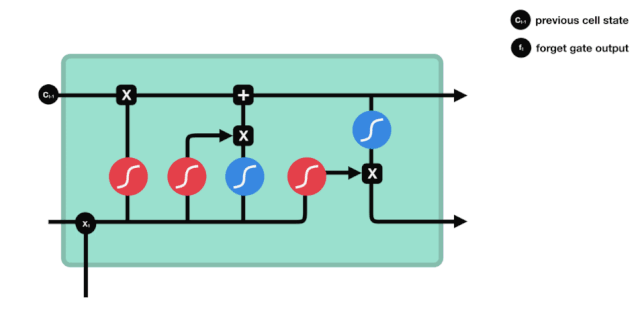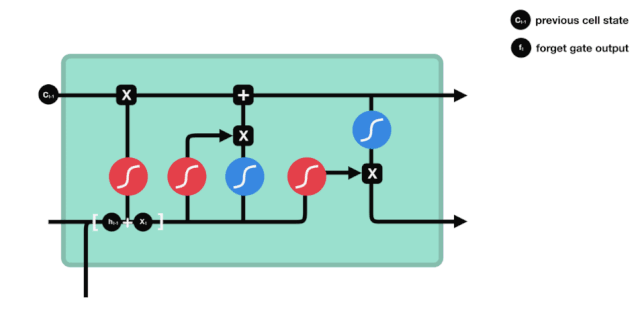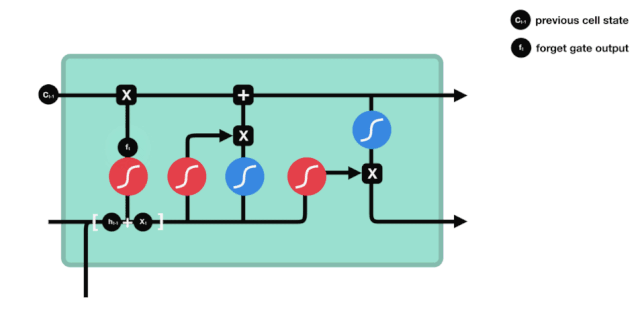
忘却ゲートは,\(h_{l-1}\)と\(x_{t}\)の情報を見て,0-1の間のベクトルを出力する.このベクトルの内の0-1の値は,細胞状態\(C_{t-1}\)の中で,どの情報が保持されるか,または廃棄されるかを示す.0は保存されない,そして1は保存される.

\(f_{t} = の数学式\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

入口

次に,細胞状態に追加する新しい情報を決定します. このステップは,入力ドアを開くことで完了します.

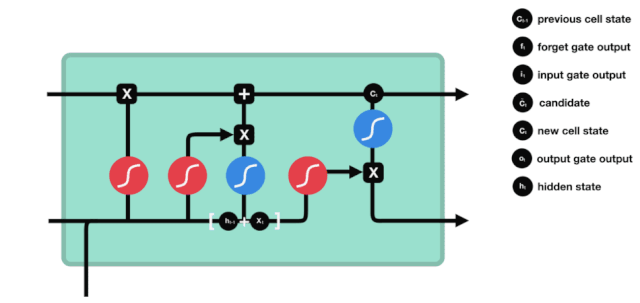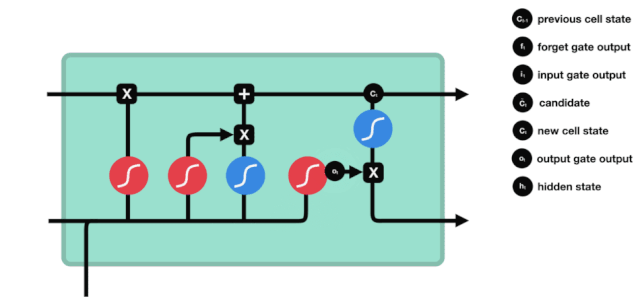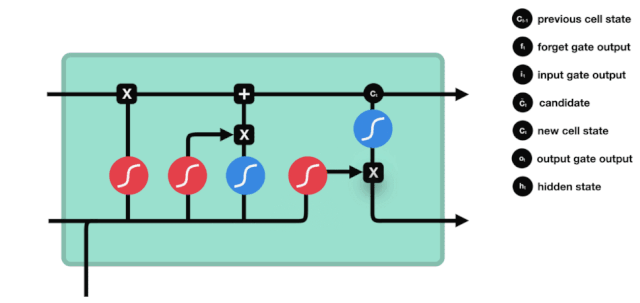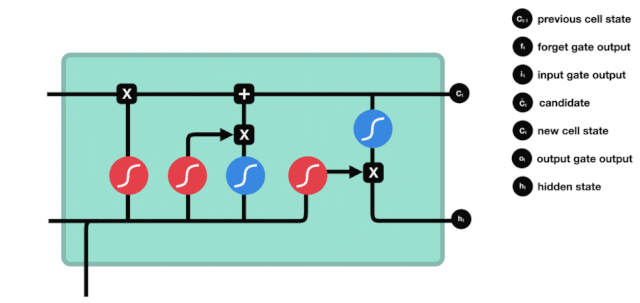
\(h_{l-1}\)と\(x_{t}\)の情報は,忘却ゲート (sigmoid) と入力ゲート (tanh) に入れられていることがわかります.忘却ゲートの出力値は0-1なので,忘却ゲートの出力値は0であれば,入力ゲート後の結果は\(C_{i}\)が現在の細胞状態に追加されることはありません.

\(C_{t}=f_{t} * C_{t-1}+i_{t} * という数学的公式が使われています.\tilde{C}_{t}\)

出口ドア

細胞状態を更新した後は,\(h_{l-1}\)と\(x_{t}\)の入力と合計に基づいて,出力細胞のどの状態特性を判断する必要がある.ここでは,出力ドアと呼ばれるシグモイド層を通過して出力状態を判断する条件を入力し,その後,出力ドアを通過して出力状態を入力し,1~1の値のベクトルを得ます.このベクトルと出力ドアからの判断条件を掛けると,最終的なRNNユニットの出力が得られます.

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

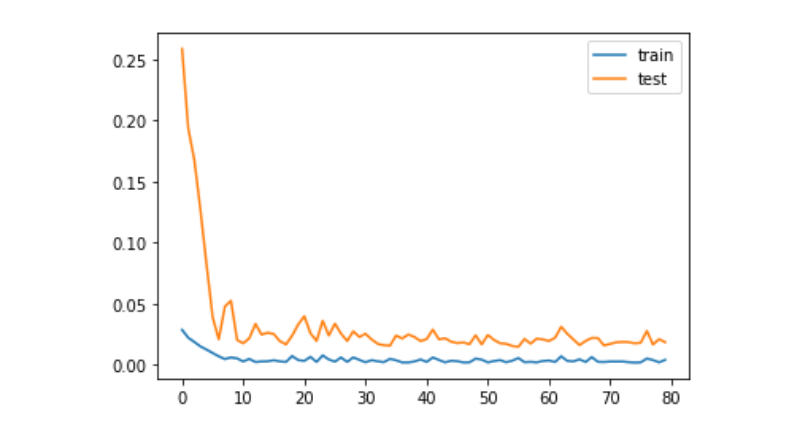
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

予測する

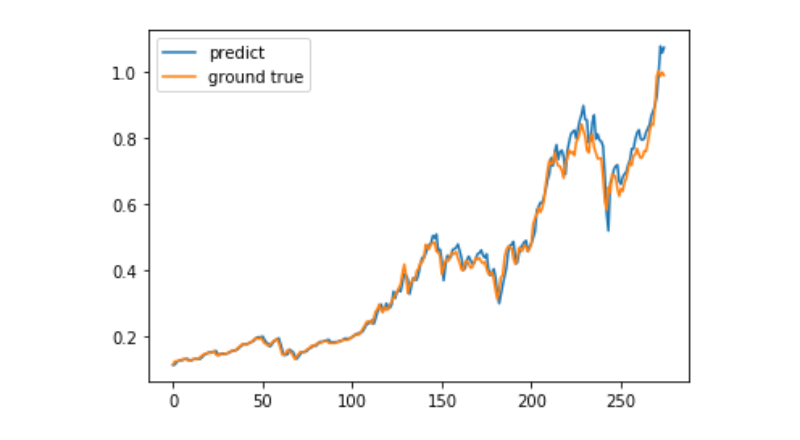
predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

現在,機械学習によるビットコインの長期価格動きの予測は非常に困難であるため,本文は学習ケースとしてのみ使用できます.このケースは,その後,メット池雲のデモ画像の中でオンラインで公開され,興味のあるユーザーは直接体験できます.