LSTM 프레임워크를 사용한 실시간 비트코인 가격 예측
 1
1
 1790
1790

참고: 이 사례는 학습 연구 용도로만 사용되며, 투자 추천은 아닙니다.
비트 코인의 가격 데이터는 시간 순서에 기초하고 있으므로 비트 코인의 가격 예측은 LSTM 모델을 주로 사용한다.
장기 단기 기억 (LSTM) 은 시간 순서 데이터 (또는 시간/공간/구조 순서를 가진 데이터, 예를 들어 영화, 문장 등) 에 특히 적합한 딥러닝 모델로, 암호화폐의 가격 방향을 예측하는 데 이상적인 모델이다.
이 글은 주로 LSTM를 통해 데이터 매칭을 통해 비트코인의 미래 가격을 예측하는 것에 관한 것입니다.
import이 필요한 라이브러리
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout
from matplotlib import pyplot as plt
%matplotlib inline
데이터 분석
데이터 로드
BTC의 일일 거래 데이터를 읽습니다.
data = pd.read_csv(filepath_or_buffer="btc_data_day")
데이터를 볼 수 있는데, 현재 총 1380개의 데이터가 있으며, 데이터는 Date, Open, High, Low, Close, Volume (BTC), Volume (Currency), Weighted Price의 열들로 구성되어 있다. 그 중 Date 열을 제외한 나머지 데이터 열은 float64 데이터 타입이다.
data.info()
다음 10줄의 데이터를 보세요.
data.head(10)
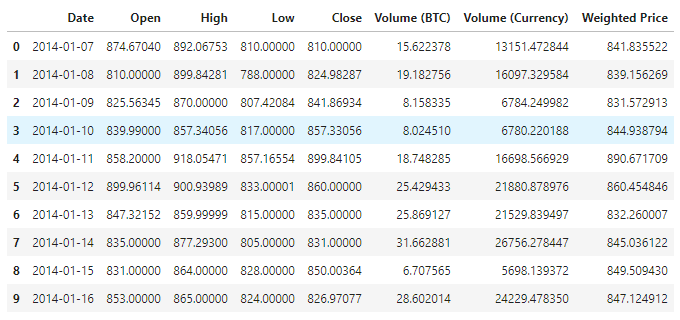
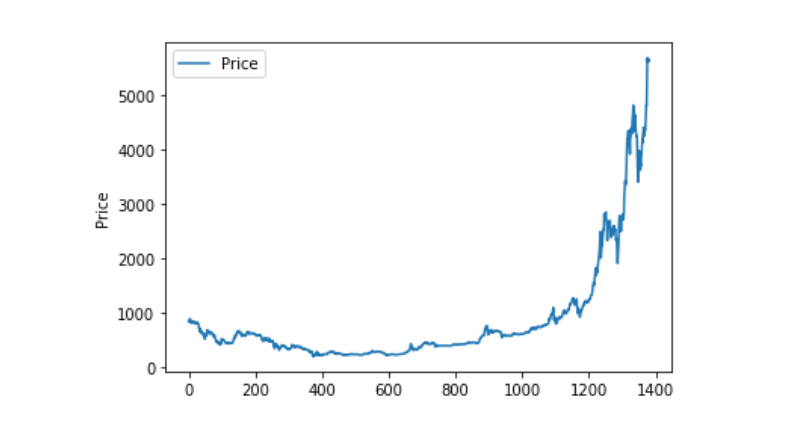
데이터 시각화
matplotlib을 사용하여 무게값을 도출하여 데이터의 분포와 흐름을 확인합니다. 이 도표에서 우리는 데이터 0의 일부를 발견하고, 데이터에 예외가 있는지 확인해야 합니다.
plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()
비정상적인 데이터 처리
이 자료에 nan이 들어있는지 확인해보면
data.isnull().sum()
Date 0
Open 0
High 0
Low 0
Close 0
Volume (BTC) 0
Volume (Currency) 0
Weighted Price 0
dtype: int64
0값을 보면 0값이 있다는 것을 알 수 있습니다
(data == 0).astype(int).any()
Date False
Open True
High True
Low True
Close True
Volume (BTC) True
Volume (Currency) True
Weighted Price True
dtype: bool
data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)
(data == 0).astype(int).any()
Date False
Open False
High False
Low False
Close False
Volume (BTC) False
Volume (Currency) False
Weighted Price False
dtype: bool
그리고 이 자료의 분포와 흐름을 보면, 이 곡선은 매우 연속적으로 나타납니다.
plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()
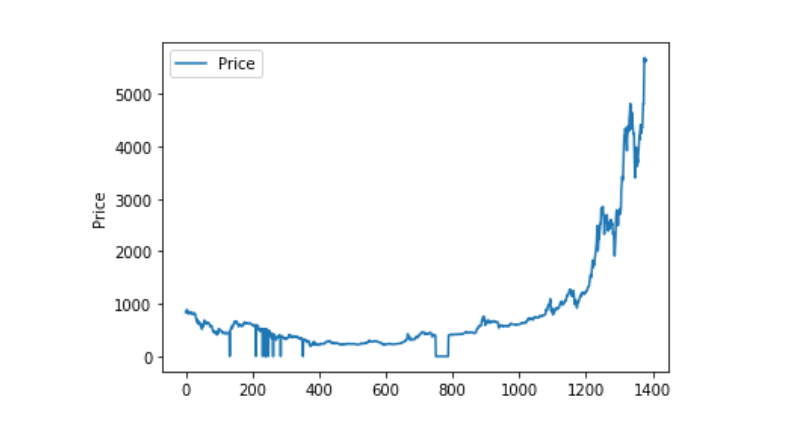
훈련 데이터 세트와 테스트 데이터 세트의 분할
0-1로 통합합니다.
data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)
테스트 데이터 세트와 트레이닝 데이터 세트를 2:8으로 나누고
ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]
훈련 데이터 세트와 테스트 데이터 세트를 만들고, 우리의 훈련 데이터 세트와 테스트 데이터 세트를 창으로 1 일 동안 만듭니다.
def create_dataset(data):
window = 1
label_index = 6
x, y = [], []
for i in range(len(data) - window):
x.append(data[i:(i + window), :])
y.append(data[i + window, label_index])
return np.array(x), np.array(y)
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)
모델 정의 및 훈련
이 경우 간단한 모델을 사용했습니다.. LSTM2. Dense。
여기서 LSTM의 inputh shape에 대해 설명할 필요가 있다. Input Shape의 입력 차원은 [[:batch_size, time steps, features]]이다. 여기서, time steps 값은 데이터 입력시의 시간 창 간격이다. 여기서 우리는 1일을 시간 창으로 사용하고, 우리의 데이터는 일일 데이터이다. 따라서 여기서 우리의 time steps는 1이다.
긴 단기 기억 (Long short-term memory, LSTM) 은 특수한 RNN이며, 주로 긴 시퀀스 훈련 과정에서梯度消失과梯度爆破 문제를 해결하기 위해 사용된다. 여기서는 LSTM에 대해 간단히 소개한다.
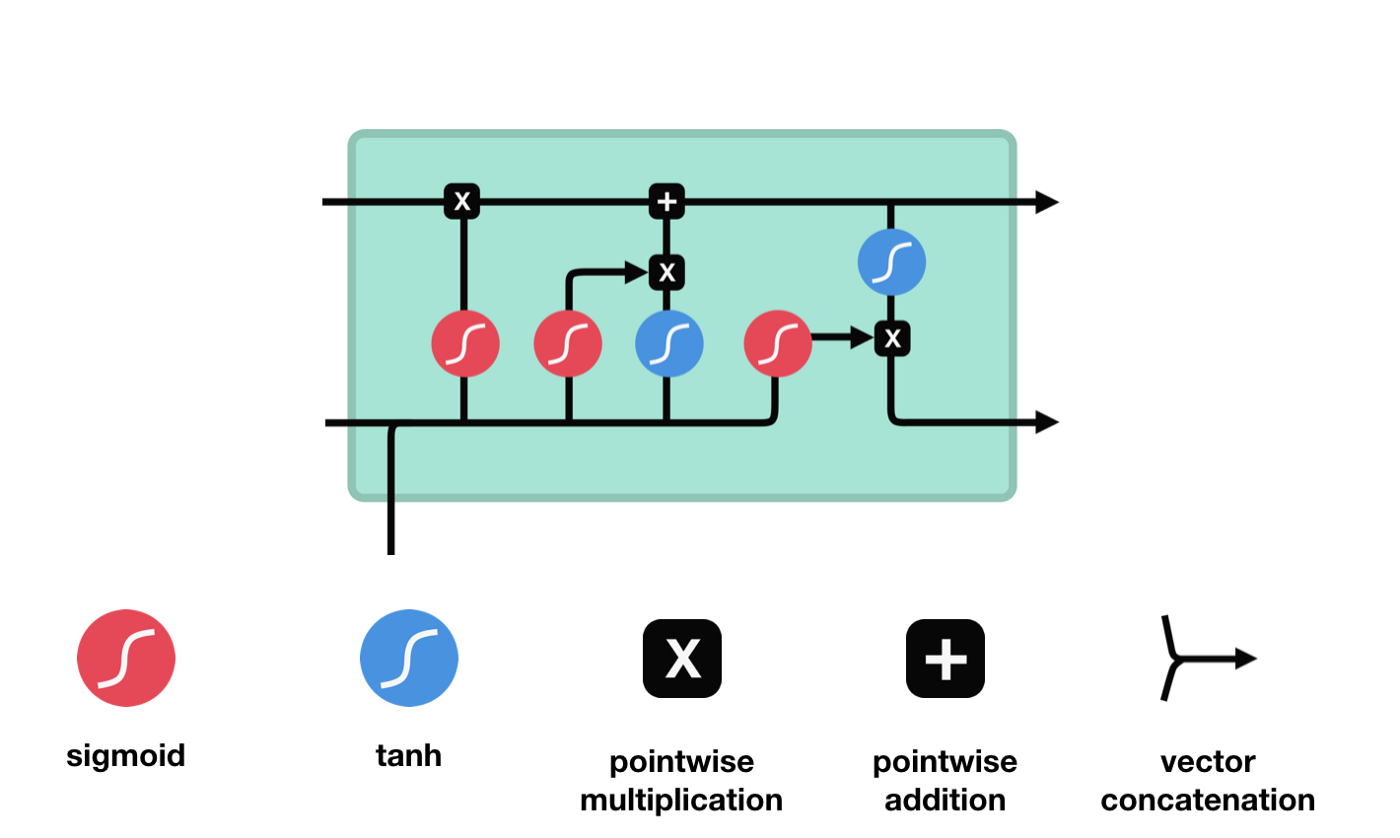
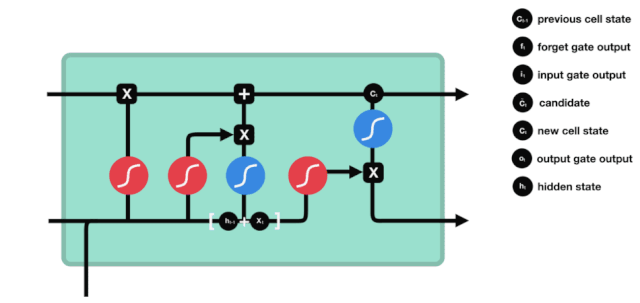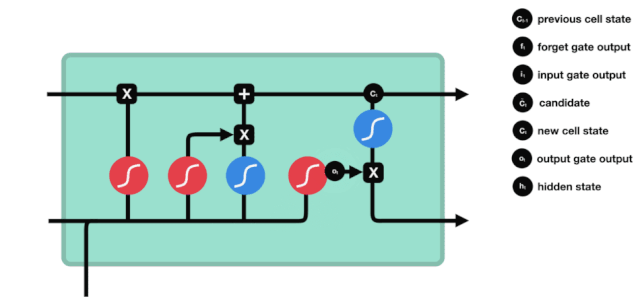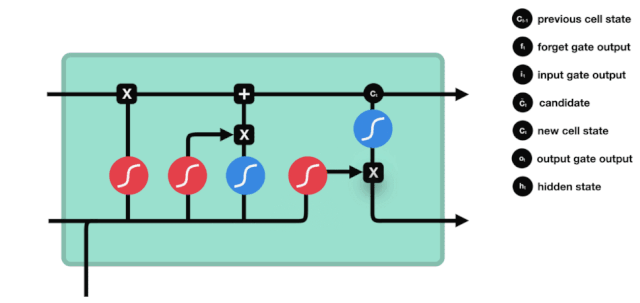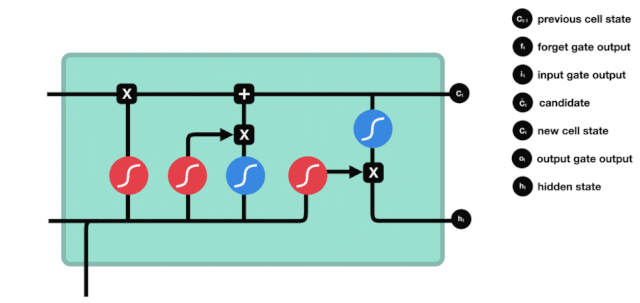
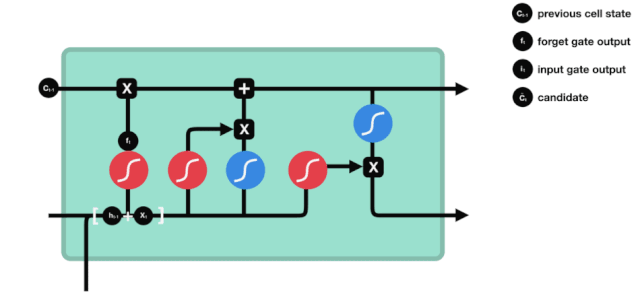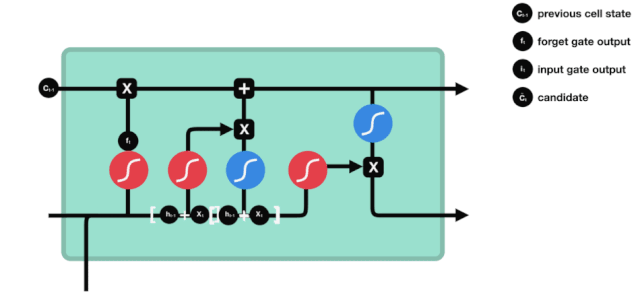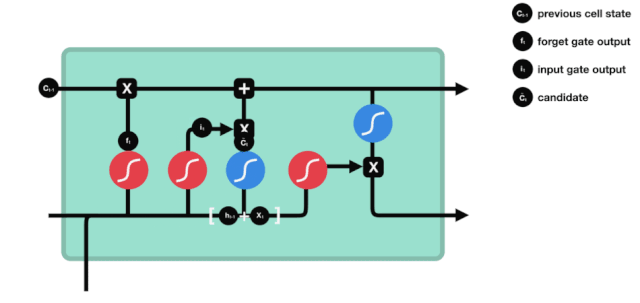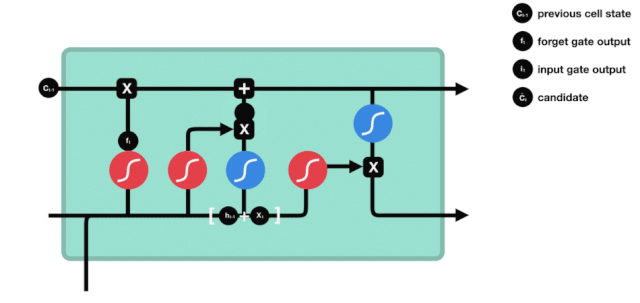
LSTM의 네트워크 구조 도표에서 볼 수 있듯이, LSTM은 실제로 작은 모델이며, 3개의 시그모이드 활성화 함수, 2개의 탕 활성화 함수, 3개의 곱셈, 1개의 덧셈을 포함하고 있다.
세포 상태
세포 상태는 LSTM의 중심에 있습니다. 그는 위의 그림에서 가장 높은 검은 선입니다. 이 검은 선 아래는 몇 개의 문이 있습니다. 우리는 나중에 소개합니다. 세포 상태는 각 문의 결과에 따라 업데이트됩니다. 우리는 아래에서 이 문들을 소개하면 세포 상태의 과정을 이해할 수 있습니다.
LSTM 네트워크는 게이트라고 불리는 구조를 통해 세포 상태에 정보를 삭제하거나 추가할 수 있다. 게이트는 선택적으로 어떤 정보가 통과하도록 결정할 수 있다. 게이트의 구조는 시그모이드 계층과 점배 operations의 조합이다. 시그모이드 계층의 출력은 0-1의 값이기 때문에 0은 통과할 수 없으며 1은 통과할 수 있다.
잊음의 문
LSTM의 첫 번째 단계는 세포 상태가 어떤 정보를 버려야 하는지를 결정하는 것입니다. 이 부분은 잊기 문이라고 불리는 시그모이드 유닛을 통해 처리됩니다.
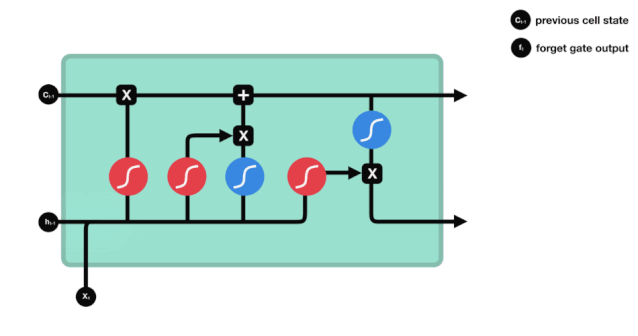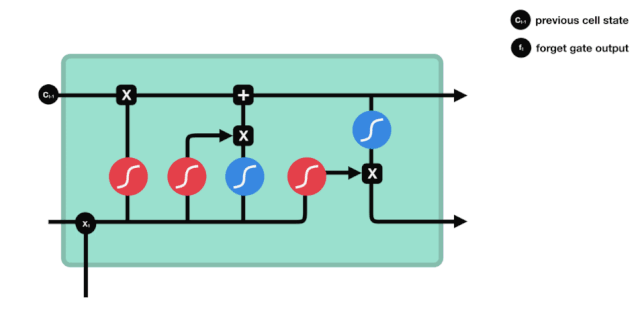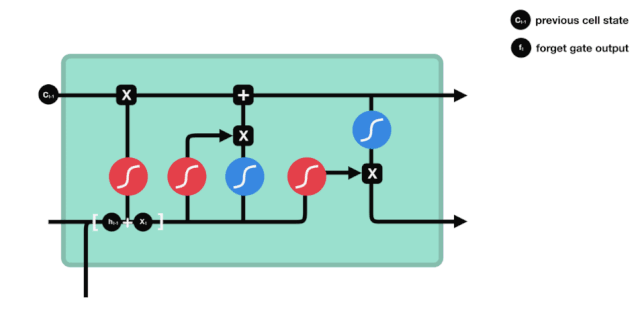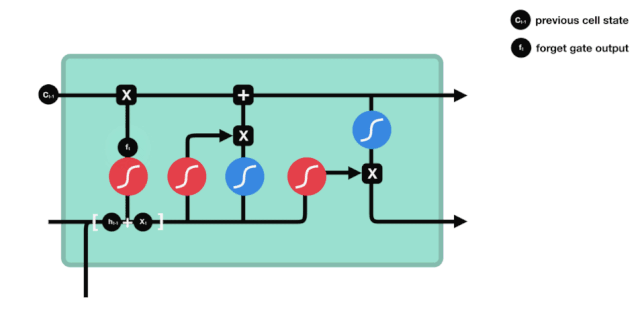
우리가 볼 수 있듯이, 망각문은 \(h_{l-1}\)와 \(x_{t}\) 정보를 보고 0-1 사이의 벡터를 출력합니다. 이 벡터 안의 0-1 값은 세포 상태 \(C_{t-1}\)에서 어떤 정보가 보존되거나 버려지는지를 나타냅니다. 0은 보존되지 않고 1은 보존됩니다.
수학 표현식: \(f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)
입구
다음 단계는 세포 상태에 어떤 새로운 정보를 추가할지 결정하는 것입니다. 이것은 입력 문을 열어서 이루어집니다.
우리는 \(h_{l-1}\)와 \(x_{t}\)의 정보가 또 하나의 방치문 ((sigmoid) 과 입력문 ((tanh) 에 넣힌 것을 보았습니다. 방치문의 출력은 0-1의 값이기 때문에, 따라서, 방치문이 0을 출력한다면, 입력문 후의 결과는 \(C_{i}\)가 현재 세포 상태에 추가되지 않을 것이며, 만약 1이라면, 모두 세포 상태에 추가될 것입니다. 따라서 여기서 방치문의 기능은 입력문의 결과를 선택적으로 세포 상태에 추가하는 것입니다.
수학 공식은 \(C_{t}=f_{t} * C_{t-1}+i_{t} * 입니다\tilde{C}_{t}\)
출구
세포 상태를 업데이트한 후 \(h_{l-1}\)와 \(x_{t}\)의 입력값에 따라 출력하는 세포의 상태 특성을 판단해야 합니다. 여기서 출력하는 세포의 상태를 출력문이라고 하는 시그모이드 계층을 통해 판단해야 합니다. 그 다음 세포 상태를 탄 계층을 통해 -1~1 사이의 값을 얻을 수 있습니다. 이 벡터와 출력문에서 얻은 판단 조건이 곱하면 최종 RNN 단위의 출력을 얻습니다.
def create_model():
model = Sequential()
model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
model.summary()
return model
model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)
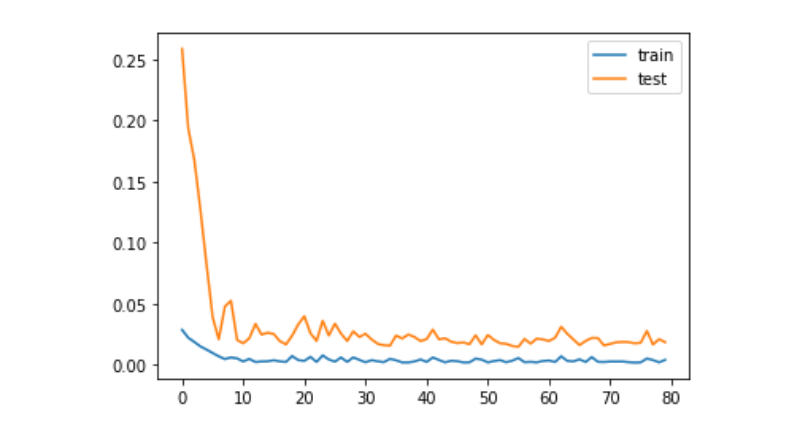
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)
예측
predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()
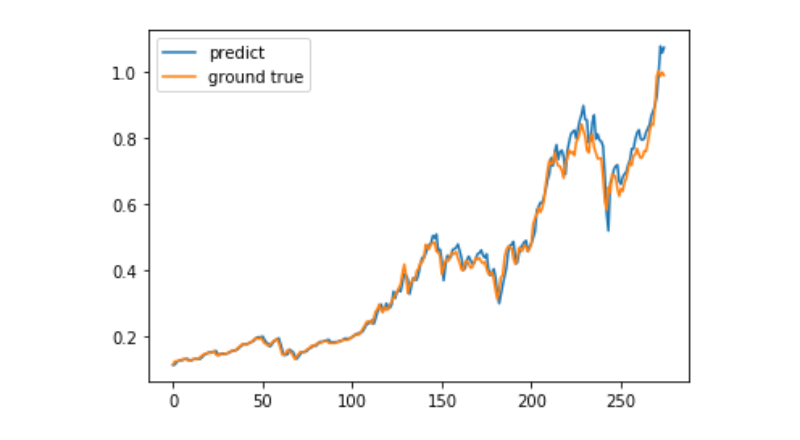
현재 머신러닝을 활용하여 비트코인의 장기적인 가격 움직임을 예측하는 것은 매우 어렵고, 이 문서는 학습 사례로만 사용할 수 있다. 이 사례는 나중에 온라인에 올라와 매트 풀 클라우드의 데모 영상 가운데, 관심 있는 사용자는 직접 체험할 수 있다.