Neste artigo, escreveremos uma estratégia de day trading. Ele usará o conceito clássico de negociação de “pares de negociação de reversão média”. Neste exemplo, utilizaremos dois fundos negociados em bolsa (ETFs), SPY e IWM, que são negociados na Bolsa de Valores de Nova York (NYSE) e tentam representar os índices do mercado de ações dos EUA, o S&P 500 e o Russell 2000. .

A estratégia cria um “carry” ao operar comprado em um ETF e vendido em outro. A relação longo-curto pode ser definida de muitas maneiras, por exemplo, usando métodos de séries temporais de cointegração estatística. Neste cenário, calcularemos a taxa de hedge entre SPY e IWM por meio de regressão linear contínua. Isso nos permitirá criar um “spread” entre SPY e IWM que é normalizado para um z-score. Quando o z-score excede um certo limite, um sinal de negociação é gerado porque acreditamos que esse “spread” retornará à média.

A justificativa para a estratégia é que tanto o SPY quanto o IWM representam aproximadamente o mesmo cenário de mercado, ou seja, o desempenho do preço das ações de um grupo de grandes e pequenas empresas dos EUA. A premissa é que se você aceitar a teoria da “reversão média” dos preços, então ela sempre reverterá, porque os “eventos” podem afetar o S&P500 e o Russell 2000 separadamente em um período muito curto de tempo, mas o “diferencial da taxa de juros” entre eles sempre retornarão à média normal, e as séries de preços de longo prazo dos dois serão sempre cointegradas.

Estratégia

A estratégia é executada da seguinte forma:

Dados - Obtenha gráficos de velas de 1 minuto do SPY e do IWM de abril de 2007 a fevereiro de 2014.

Processamento - Alinhe os dados corretamente e exclua as barras que estão faltando umas nas outras. (Se um lado estiver faltando, ambos os lados serão excluídos)

Spread - A taxa de hedge entre dois ETFs é calculada usando uma regressão linear contínua. Definido como o coeficiente de regressão beta usando uma janela de lookback que é movida para frente em 1 barra e o coeficiente de regressão é recalculado. Portanto, a taxa de cobertura βi, bi K-line é usada para traçar a K-line calculando o ponto de cruzamento de bi-1-k para bi-1.

Z-Score - O valor do Standard Spread é calculado da maneira usual. Isso significa subtrair a média da dispersão (amostra) e dividir pelo desvio padrão da dispersão (amostra). O motivo para fazer isso é tornar o parâmetro limite mais fácil de entender, já que o Z-Score é uma quantidade adimensional. Introduzi intencionalmente o “viés de previsão” nos cálculos para mostrar o quão sutil ele pode ser. Experimente!

Negociação - Sinais longos são gerados quando o valor negativo do z-score cai abaixo de um limite predeterminado (ou pós-otimizado), enquanto sinais curtos são gerados no sentido oposto. Quando o valor absoluto do z-score cai abaixo de um limite adicional, um sinal para fechar a posição é gerado. Para esta estratégia, eu (de forma um tanto arbitrária) escolhi |z| = 2 como o limite de entrada e |z| = 1 como o limite de saída. Supondo que a reversão à média desempenhe um papel no spread, esperamos que o exposto acima capture essa relação de arbitragem e forneça um bom lucro.

Talvez a melhor maneira de entender profundamente uma estratégia seja realmente implementá-la. A seção a seguir detalha o código Python completo (arquivo único) usado para implementar essa estratégia de reversão à média. Adicionei comentários detalhados ao código para ajudar você a entender melhor.

Implementação Python

Como em todos os tutoriais Python/pandas, seu ambiente Python deve ser configurado conforme descrito neste tutorial. Após a configuração estar concluída, a primeira tarefa é importar as bibliotecas Python necessárias. Isso é necessário para usar matplotlib e pandas.

As versões específicas da biblioteca que estou usando são as seguintes:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

Vamos em frente e importar estas bibliotecas:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

A função a seguir create_pairs_dataframe importa dois arquivos CSV contendo os candlesticks intradiários de dois símbolos. No nosso caso, seriam SPY e IWM. Em seguida, ele cria um “par de quadros de dados” separado que usa os índices de ambos os arquivos originais. Os registros de data e hora podem variar devido a transações perdidas e erros. Esse é um dos principais benefícios de usar uma biblioteca de análise de dados como o Pandas. Lidamos com código “clichê” de uma forma muito eficiente.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

O próximo passo é fazer uma regressão linear contínua entre SPY e IWM. Neste cenário, IWM é o preditor (‘x’) e SPY é a resposta (‘y’). Eu defini uma janela de lookback padrão de 100 velas. Como mencionado acima, esses são os parâmetros da estratégia. Para que uma estratégia seja considerada robusta, o ideal é ver um relatório de retorno que seja convexo ao longo do período de retrospectiva (ou alguma outra medida de desempenho). Portanto, em um estágio posterior do código, realizaremos uma análise de sensibilidade variando o período de retrospectiva dentro do escopo.

Depois de calcular os coeficientes beta contínuos no modelo de regressão linear para SPY-IWM, adicione-o ao par DataFrame e remova as linhas vazias. Isso constrói o primeiro conjunto de velas, que é igual à medida aparada do comprimento do lookback. Em seguida, criamos um spread entre os dois ETFs, uma unidade de SPY e uma unidade de -βi de IWM. Obviamente, esse não é um cenário realista, pois estamos empregando uma pequena quantidade de IWM, o que não é possível em uma implementação prática.

Por fim, criamos o z-score do spread, calculado subtraindo a média do spread e normalizando pelo desvio padrão do spread. É importante notar que há um “viés prospectivo” bastante sutil em ação aqui. Deixei isso no código intencionalmente porque queria destacar o quão fácil é cometer erros como esse em pesquisas. Calcule a média e o desvio padrão de toda a série temporal de dispersão. Se a intenção é refletir a verdadeira precisão histórica, então essa informação não pode ser obtida porque utiliza implicitamente informações do futuro. Portanto, devemos usar a média móvel e o desvio padrão para calcular o escore z.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Em create_long_short_market_signals, crie sinais de negociação. Eles são calculados medindo o valor do escore z que excede um limite. Quando o valor absoluto do z-score é menor ou igual a outro limite (menor), é dado um sinal para fechar a posição.

Para conseguir isso, é necessário estabelecer se a estratégia de negociação é de “abertura” ou “fechamento” para cada linha K. Long_market e short_market são duas variáveis ​​definidas para rastrear posições longas e curtas. Infelizmente, é computacionalmente lento, pois é muito mais simples programar de forma iterativa do que uma abordagem vetorizada. Embora um gráfico de velas de 1 minuto exija ~700.000 pontos de dados por arquivo CSV, ainda é relativamente rápido de calcular no meu antigo desktop!

Para iterar sobre um DataFrame do pandas (uma operação reconhecidamente incomum), é necessário usar o método iterrows, que fornece um gerador iterável:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Nesta fase, atualizamos os pares para conter os sinais longos e curtos reais, o que nos permite determinar se precisamos abrir uma posição. Agora precisamos criar um portfólio para rastrear o valor de mercado das posições. A primeira tarefa é criar uma coluna de posição que combine sinais longos e curtos. Isso conterá uma lista de elementos de (1,0,-1), onde 1 representa uma posição longa, 0 representa nenhuma posição (que deve ser fechada) e -1 representa uma posição curta. As colunas sym1 e sym2 representam o valor de mercado das posições SPY e IWM no final de cada candle.

Uma vez criados os valores de mercado do ETF, nós os somamos para produzir o valor total de mercado no final de cada vela. Ele é então convertido em um valor de retorno por meio do método pct_change desse objeto. As linhas subsequentes de código limpam entradas errôneas (elementos NaN e inf) e, finalmente, calculam a curva de patrimônio completa.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

A função principal une tudo. Os arquivos CSV intradiários estão localizados no caminho datadir. Certifique-se de modificar o código a seguir para apontar para seu diretório específico.

Para determinar o quão sensível a estratégia é ao período de lookback, é necessário calcular uma série de métricas de desempenho de lookback. Selecionei a porcentagem de retorno total final do portfólio como métrica de desempenho e o intervalo de retrospectiva.[50.200] com um incremento de 10. Você pode ver no código abaixo que a função anterior é encapsulada em um loop for nesse intervalo e os outros limites permanecem os mesmos. A tarefa final é criar um gráfico de linhas de lookbacks versus retornos usando matplotlib:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

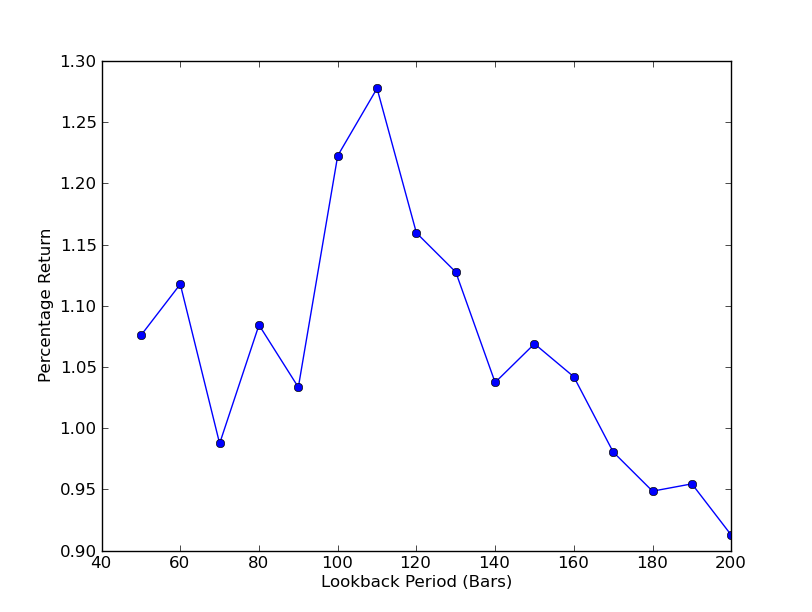
Agora você pode ver um gráfico dos lookbacks e retornos. Observe que há um máximo “global” para lookbacks, igual a 110 barras. Se vemos uma situação em que os lookbacks não têm nada a ver com retornos, é porque:

Análise de sensibilidade do período de lookback da taxa de hedge de regressão linear SPY-IWM

Nenhum artigo de backtesting estaria completo sem uma curva de lucro com inclinação ascendente! Então, se você quiser traçar os retornos de lucro acumulados em função do tempo, você pode usar o código a seguir. Ele traçará o portfólio final gerado a partir do estudo do parâmetro lookback. Portanto, é necessário escolher o lookback de acordo com o gráfico que você deseja visualizar. Este gráfico também mostra os retornos do SPY no mesmo período para ajudar na comparação:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

O gráfico da curva de patrimônio líquido abaixo tem um período de retrospectiva de 100 dias:

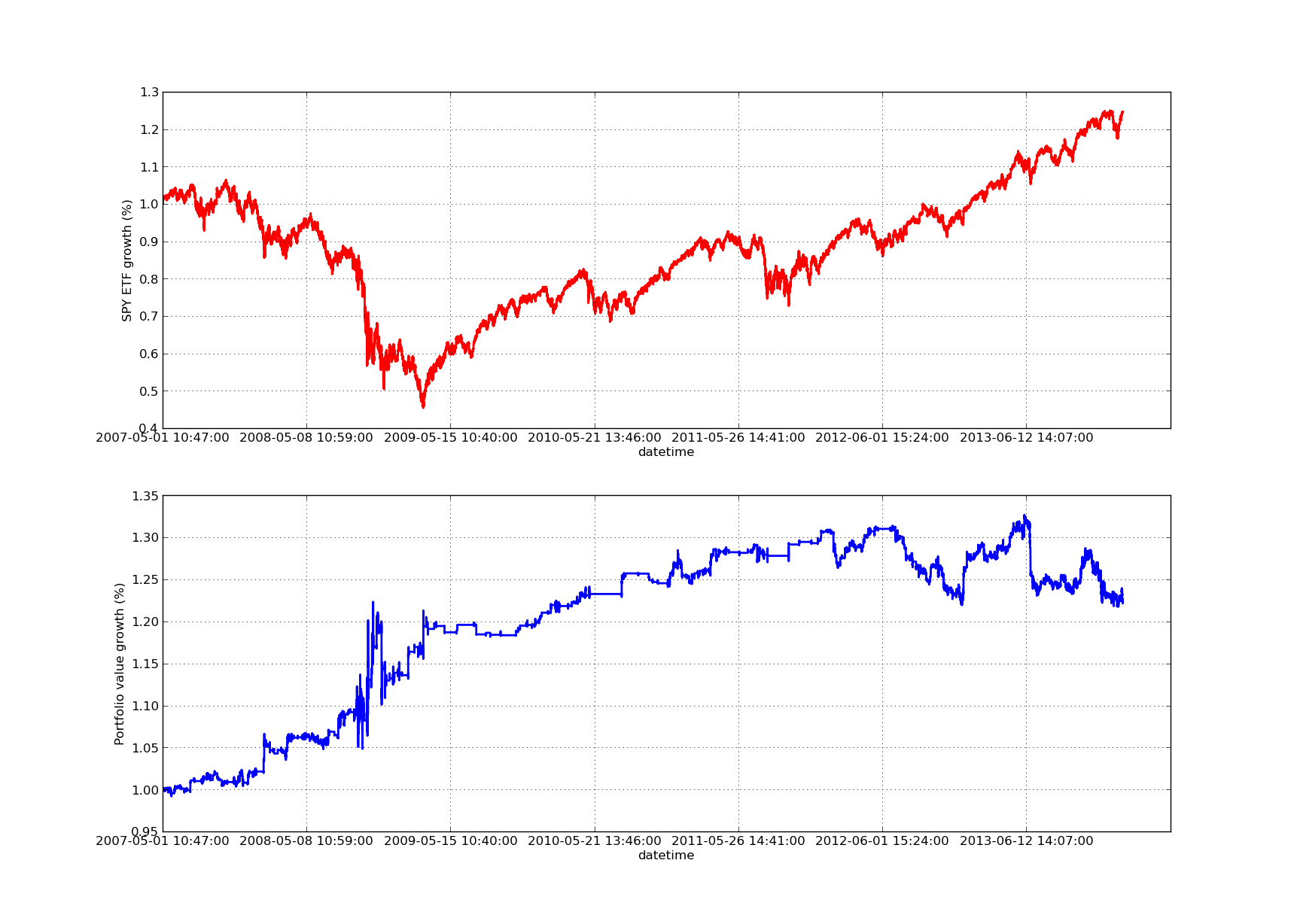
Análise de sensibilidade do período de lookback da taxa de hedge de regressão linear SPY-IWM

Observe que a redução do SPY foi bastante grande em 2009, durante a crise financeira. A estratégia também passa por um período turbulento durante esta fase. Observe também que o desempenho se deteriorou no último ano devido à natureza de forte tendência do SPY durante esse período, refletindo o S&P 500.

Observe que ainda precisamos levar em conta o “viés de previsão” ao calcular a dispersão do z-score. Além disso, todos esses cálculos são realizados sem custos de transação. Quando esses fatores são levados em consideração, essa estratégia tende a ter um desempenho ruim. Tanto as taxas quanto o slippage ainda estão indeterminados. Além disso, a estratégia negocia em unidades fracionárias do ETF, o que também é altamente irrealista.

Em um artigo futuro, criaremos um backtester mais complexo, orientado a eventos, que levará todos os itens acima em consideração, dando-nos mais confiança em nossa curva de patrimônio e indicadores de desempenho.