Заявление об авторском праве: Если вы хотите перевести код статьи, укажите источник, если вы используете его для коммерческих целей, напишите статью, пожалуйста, лично или свяжитесь с автором по электронной почте [email protected]

1. Введение

Преимущества количественных сделок

Количественная торговля - это субъективная оценка, основанная на передовых математических моделях вместо человеческих суждений, использование компьютерных технологий для разработки стратегии, которая позволяет использовать множество событий, которые приносят дополнительную прибыль, чтобы значительно снизить влияние колебаний настроения инвесторов и избежать нерациональных инвестиционных решений в условиях чрезмерного ажиотажа или пессимизма на рынке.                                          *7 часов непрерывной последовательности рынка сделок, и количественные сделки могут достичь эффекта высокочастотных сделок, начиная с рынка цифровых валют, очевидно, это хороший старт для количественных сделок. В настоящее время рынок цифровых валют все еще не созрел.

Описание модели GQNR

Эта модель, основанная на модели Гарча, использует нелинейную регрессию, например, GA, для прогнозирования верхнего VaR и нижнего VaR в будущем следующем цикле. В дальнейшем эта модель будет называться GQNR.

Модуль Garch 1.

        В этом разделе будет подробно рассказано о выводах из центральной части стратегии Garch, которая имеет некоторое распространение на финансовых рынках и может достичь некоторого прогнозирующего эффекта в цифровых валютах.

1.1 Определение Garch

        Суть модели ARCH заключается в том, чтобы использовать последовательность остаточных квадратов для перемещения в q-этап для приведения значения текущей дифференциальной функции. Поскольку модель перемещаемого среднего значения имеет степень предела q для коэффициентов самосоотношения, модель ARCH фактически применима только к краткосрочным коэффициентам самосоотношения дифференциальной функции.          Но на практике, некоторые дифференциальные функции остаточных последовательностей имеют долгосрочную саморегулируемость, при этом использование дифференциальных функций ARCH-модели для приспособления к ARCH-модели приведет к высоким скользящим средним степеням, увеличит сложность оценки параметров и в конечном итоге повлияет на точность приспособления ARCH-модели.                                                                                        Модель GARCH фактически была создана на основе ARCH с добавлением регрессивности p-класса, учитывающей дифференциальную функцию, которая может эффективно приспосабливаться к дифференциальной функции с долговременной памятью. Модель ARCH является особым примером модели GARCH, моделью GARCH с p = 0 (p,q).

1.2 Процесс ARCH

       определяется как σn в n-1 торговом цикле, оценивая колебания активов в n-м торговом цикле, и mu - ежедневная доходность, то можно сделать непредвзятую оценку на основе доходности за последние m торговых циклов: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(        ; сделайте следующие изменения: 1 переведите μn-i в процентную доходность; 2 переведите m-1 в m; 3 предположим, что μ = 0, и эти изменения не сильно влияют на результат. В соответствии с вышеприведенной формулой волатильность может быть упрощена до: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         то есть квадрат колебаний в каждом цикле имеет равновесие 1/m, так как это оценка текущих колебаний, ближайшие данные должны быть приданы более высокий вес, то формула может быть изменена на: \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi - это коэффициент квадрата доходности на третий торговый цикл i, принимая положительные значения, и чем меньше i, тем больше сумма весов равна 1. Дальнейшее распространение, предполагая существование долгосрочной дифференциации VL, и соответствующий вес -γ, можно получить по вышеуказанному выражению:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        О = γVL, формула(15) можно переписать как: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\(         В соответствии с вышеизложенным мы можем получить обычный ARCH(1) процесс \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 Процесс GARCH

Модель GARCH (p,q) является комбинацией моделей ARCH (p) и EWMA (q), что означает, что волатильность связана не только с доходами предыдущего периода p, но и с предыдущим периодом q, выраженной следующим образом: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         В соответствии с вышеуказанным выражением мы можем получить общепринятый GARCH ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 модуля QR

        В этом разделе будет изложены основные детали регрессии, описывающие важность стратегических детали

2.1 Определение QR

Диаметрическая регрессия - это метод моделирования, который предполагает линейную связь между множеством регрессивных переменных X и диаметрией объясняемой переменной Y. Предыдущие модели регрессии фактически изучали условные ожидания объясняемой переменной. Также люди интересовались, как объясняемая переменная связана со средним числом распределения объясняемой переменной. Это было впервые предложено Koenker и Bassett в 1978 году.

2.2 От OLS к QR

        Общий метод регрессии - это кратность наименьшей двойной, то есть квадрат суммы минимизации погрешности: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         а целью дроби является минимизация взвешенной погрешности на основе вышеуказанных формул: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 Визуализация QR

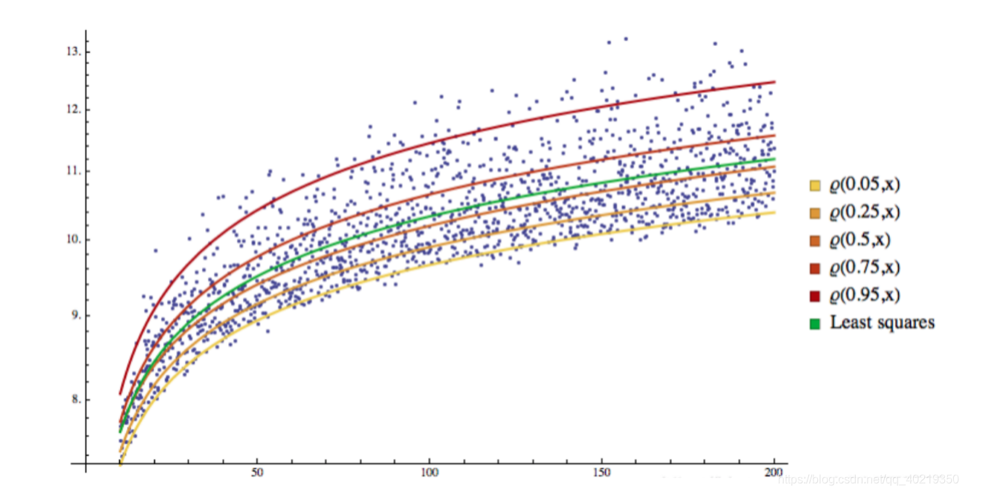
3. ГАРХ-QR возвращается

Мы, естественно, подумали, можно ли использовать неизвестную рыночную волатильность сигмы с дефицитером Q, то есть VaR, для прогнозирования волатильных отклонений в будущем при высокой вероятности, что этот сектор будет развиваться в этом направлении.

3.1 Выбор формы регрессии для колебаний и VaR

        Поскольку здесь речь идет о стратегическом ядре, я пока покажу форму, чтобы проиллюстрировать свою мысль. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Определение целевой функции

        Исходя из вышеуказанной информации, мы можем комбинировать и получить конечную целевую функцию для оптимизации: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Оптимизация целевых функций с помощью машинного обучения

Этот шаг является более выборочным, традиционная степень уменьшается, но также можно использовать генетические алгоритмы, и читатели могут использовать свои творческие способности для экспериментов.Есть что-то об алгоритме GA

В-третьих, как использовать GQNR в количественном измерении

1. Определение идей

        Грузость GQNR заключается в том, что волатильность рынка, в каждой текущей точке времени, может быть прогнозирована через GARCH для прогноза волатильности следующего периода, с другой стороны, через прошедшие данные прогнозирования волатильности, может быть получено через десятичную регрессию волатильности, которая в большинстве случаев не будет превышать волатильность порог верхней границы и нижней границы.

2. Трудности использования

• Форма регрессии
• Выбор адаптивного алгоритма
• Правильные параметры для машинного обучения
• Неопределенность рынка

Решение 3.

• Сокращение циклов обучения стратегии
• Снижение долгосрочного риска по одному депозиту
• Добавление совместной проверки двойной равнолинейной тенденции и подтверждение вторичной пониженности