В этой статье мы напишем стратегию дневной торговли. Он будет использовать классическую торговую концепцию «торговых пар с возвратом к среднему». В этом примере мы будем использовать два биржевых фонда (ETF), SPY и IWM, которые торгуются на Нью-Йоркской фондовой бирже (NYSE) и пытаются представлять индексы фондового рынка США, S&P 500 и Russell 2000. .

Стратегия создает «керри» путем покупки одного ETF и продажи другого. Соотношение длинных и коротких позиций можно определить разными способами, например, с помощью методов статистической коинтеграции временных рядов. В этом сценарии мы рассчитаем коэффициент хеджирования между SPY и IWM с помощью скользящей линейной регрессии. Это позволит нам создать «разброс» между SPY и IWM, нормализованный по z-оценке. Когда z-оценка превышает определенный порог, генерируется торговый сигнал, поскольку мы считаем, что этот «спред» вернется к среднему значению.

Обоснование стратегии заключается в том, что и SPY, и IWM представляют собой примерно один и тот же рыночный сценарий, а именно динамику цен акций группы крупных и мелких компаний США. Предпосылка заключается в том, что если вы принимаете теорию «возврата к среднему» цен, то они всегда будут возвращаться, поскольку «события» могут повлиять на S&P500 и Russell 2000 по отдельности в очень короткий период времени, но «разница в процентных ставках» между они всегда будут возвращаться к нормальному среднему значению, а долгосрочные ценовые ряды этих двух показателей всегда будут коинтегрированы.

Стратегия

Стратегия реализуется следующим образом:

Данные — получите 1-минутные графики свечей SPY и IWM с апреля 2007 года по февраль 2014 года.

Обработка — правильно выровняйте данные и удалите несоответствующие друг другу столбцы. (Если одна сторона отсутствует, обе стороны будут удалены)

Спред — коэффициент хеджирования между двумя ETF рассчитывается с использованием скользящей линейной регрессии. Определяется как коэффициент бета-регрессии с использованием окна ретроспективного анализа, которое сдвигается вперед на 1 бар, а коэффициент регрессии пересчитывается. Таким образом, коэффициент хеджирования βi, bi K-line используется для отслеживания K-линии путем расчета точки пересечения от bi-1-k к bi-1.

Z-счет — значение стандартного спреда рассчитывается обычным способом. Это означает вычитание среднего значения разброса (выборки) и деление на стандартное отклонение разброса (выборки). Это делается для того, чтобы сделать пороговый параметр более понятным, поскольку Z-оценка является безразмерной величиной. Я намеренно ввел в расчеты «смещение взгляда вперед», чтобы показать, насколько оно может быть тонким. Попробуйте!

Торговля — длинные сигналы генерируются, когда отрицательное значение z-оценки падает ниже заранее определенного (или постоптимизированного) порогового значения, в то время как короткие сигналы генерируются в обратном порядке. Когда абсолютное значение z-оценки падает ниже дополнительного порога, генерируется сигнал на закрытие позиции. Для этой стратегии я (несколько произвольно) выбрал |z| = 2 в качестве порога входа и |z| = 1 в качестве порога выхода. Если предположить, что возврат к среднему значению играет роль в спреде, то, как мы надеемся, вышеприведенное выражение отразит эту арбитражную взаимосвязь и обеспечит хорошую прибыль.

Возможно, лучший способ глубоко понять стратегию — это реализовать ее на практике. В следующем разделе подробно описан полный код Python (отдельный файл), используемый для реализации этой стратегии возврата к среднему. Я добавил подробные комментарии к коду, чтобы помочь вам лучше понять его.

Реализация Python

Как и во всех руководствах по Python/pandas, ваша среда Python должна быть настроена так, как описано в этом руководстве. После завершения настройки первой задачей станет импорт необходимых библиотек Python. Это необходимо для использования matplotlib и pandas.

Конкретные версии библиотек, которые я использую, следующие:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

Давайте продолжим и импортируем эти библиотеки:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Следующая функция create_pairs_dataframe импортирует два CSV-файла, содержащие внутридневные свечи двух символов. В нашем случае это будут SPY ​​и IWM. Затем создается отдельная «пара фреймов данных», которая использует индексы обоих исходных файлов. Их временные метки могут отличаться из-за пропущенных транзакций и ошибок. Это одно из главных преимуществ использования библиотеки анализа данных, такой как pandas. Мы обрабатываем «шаблонный» код очень эффективно.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Следующий шаг — выполнение скользящей линейной регрессии между SPY и IWM. В этом сценарии IWM является предиктором («x»), а SPY — ответом («y»). Я установил окно ретроспективного анализа по умолчанию в 100 свечей. Как уже упоминалось выше, это параметры стратегии. Для того чтобы стратегия считалась надежной, в идеале нам хотелось бы видеть отчет о доходности, который является выпуклым за период ретроспективного анализа (или какой-либо другой показатель эффективности). Поэтому на более позднем этапе разработки кода мы проведем анализ чувствительности, варьируя период ретроспективного анализа в пределах области действия.

После вычисления коэффициентов скользящей бета в модели линейной регрессии для SPY-IWM добавьте ее в пару DataFrame и удалите пустые строки. Это создает первый набор свечей, который равен урезанному показателю длины ретроспективного анализа. Затем мы создали спред между двумя ETF: одну единицу SPY и одну единицу -βi IWM. Очевидно, что это нереалистичный сценарий, поскольку мы используем небольшое количество IWM, что невозможно при практической реализации.

Наконец, мы создаем z-оценку спреда, рассчитываемую путем вычитания среднего значения спреда и нормализации по стандартному отклонению спреда. Важно отметить, что здесь имеет место довольно тонкий «предвзятый подход». Я намеренно оставил это в коде, потому что хотел подчеркнуть, как легко допустить подобные ошибки в исследованиях. Рассчитайте среднее значение и стандартное отклонение всего временного ряда спреда. Если это призвано отразить истинную историческую точность, то эту информацию невозможно получить, поскольку она неявно использует информацию из будущего. Поэтому для расчета z-оценки следует использовать скользящее среднее и стандартное отклонение.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

В create_long_short_market_signals создайте торговые сигналы. Они рассчитываются путем измерения значения z-оценки, превышающего пороговое значение. Когда абсолютное значение z-оценки меньше или равно другому (меньшему) пороговому значению, подается сигнал на закрытие позиции.

Чтобы добиться этого, необходимо установить, является ли торговая стратегия «открывающей» или «закрывающей» для каждой К-линии. Long_market и short_market — две переменные, определенные для отслеживания длинных и коротких позиций. К сожалению, это медленный вычислительный процесс, поскольку его гораздо проще программировать итеративным способом, чем векторизованным. Несмотря на то, что для графика свечей с интервалом в 1 минуту требуется около 700 000 точек данных на один CSV-файл, его все равно можно относительно быстро рассчитать на моем старом компьютере!

Для итерации по DataFrame pandas (очевидно, необычная операция) необходимо использовать метод iterrows, который предоставляет итерируемый генератор:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

На этом этапе мы обновляем пары, чтобы они содержали фактические длинные и короткие сигналы, что позволяет нам определить, нужно ли нам открывать позицию. Теперь нам необходимо создать портфель для отслеживания рыночной стоимости позиций. Первая задача — создать столбец позиций, объединяющий длинные и короткие сигналы. Он будет содержать список элементов из диапазона (1,0,-1), где 1 представляет длинную позицию, 0 представляет отсутствие позиции (которую следует закрыть), а -1 представляет короткую позицию. Столбцы sym1 и sym2 представляют рыночную стоимость позиций SPY и IWM в конце каждой свечи.

После того, как рыночные стоимости ETF созданы, мы суммируем их, чтобы получить общую рыночную стоимость в конце каждой свечи. Затем он преобразуется в возвращаемое значение с помощью метода pct_change этого объекта. Последующие строки кода очищают ошибочные записи (элементы NaN и inf) и, наконец, вычисляют полную кривую капитала.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Основная функция связывает все это воедино. Внутридневные CSV-файлы находятся в каталоге datadir. Обязательно измените следующий код так, чтобы он указывал на ваш конкретный каталог.

Чтобы определить, насколько чувствительна стратегия к периоду ретроспективного анализа, необходимо рассчитать ряд показателей эффективности ретроспективного анализа. В качестве показателя эффективности и диапазона ретроспективного анализа я выбрал итоговый процент общей доходности портфеля.[50,200] с шагом 10. В коде ниже вы можете видеть, что предыдущая функция заключена в цикл for по этому диапазону, а другие пороговые значения остаются прежними. Последняя задача — создать линейный график зависимости ретроспективных данных от доходности с помощью matplotlib:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

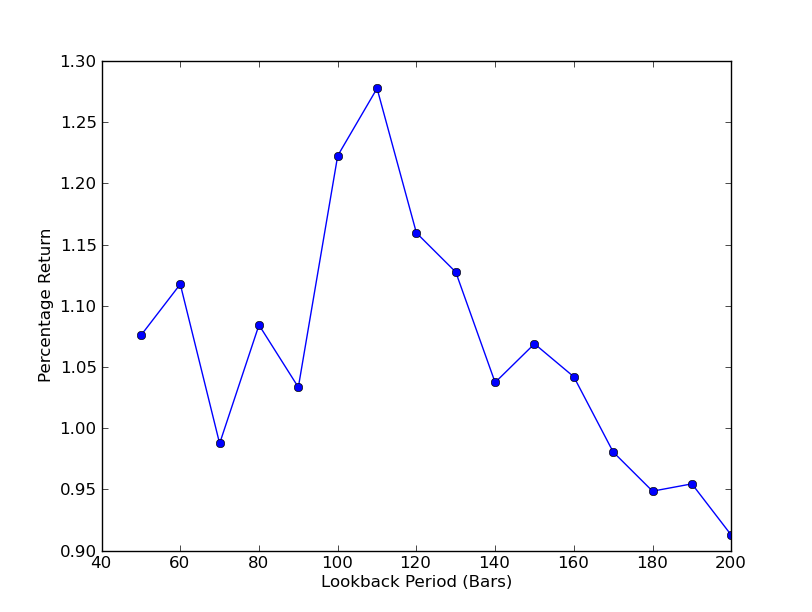
Теперь вы можете увидеть график ретроспективных оценок и доходности. Обратите внимание, что для ретроспективных анализов существует «глобальный» максимум, равный 110 барам. Если мы видим ситуацию, когда ретроспективный анализ не имеет ничего общего с доходностью, то это происходит по следующим причинам:

Анализ чувствительности коэффициента хеджирования линейной регрессии SPY-IWM за период обратного просмотра

Ни одна статья о бэктестинге не будет полной без восходящей кривой прибыли! Итак, если вы хотите построить график зависимости совокупной прибыли от времени, вы можете использовать следующий код. Он построит окончательный портфель, сформированный на основе ретроспективного исследования параметров. Поэтому необходимо выбирать ретроспективный анализ в соответствии с диаграммой, которую вы хотите визуализировать. На этой диаграмме также отображена доходность SPY за тот же период для облегчения сравнения:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

График кривой капитала ниже имеет период ретроспективного анализа 100 дней:

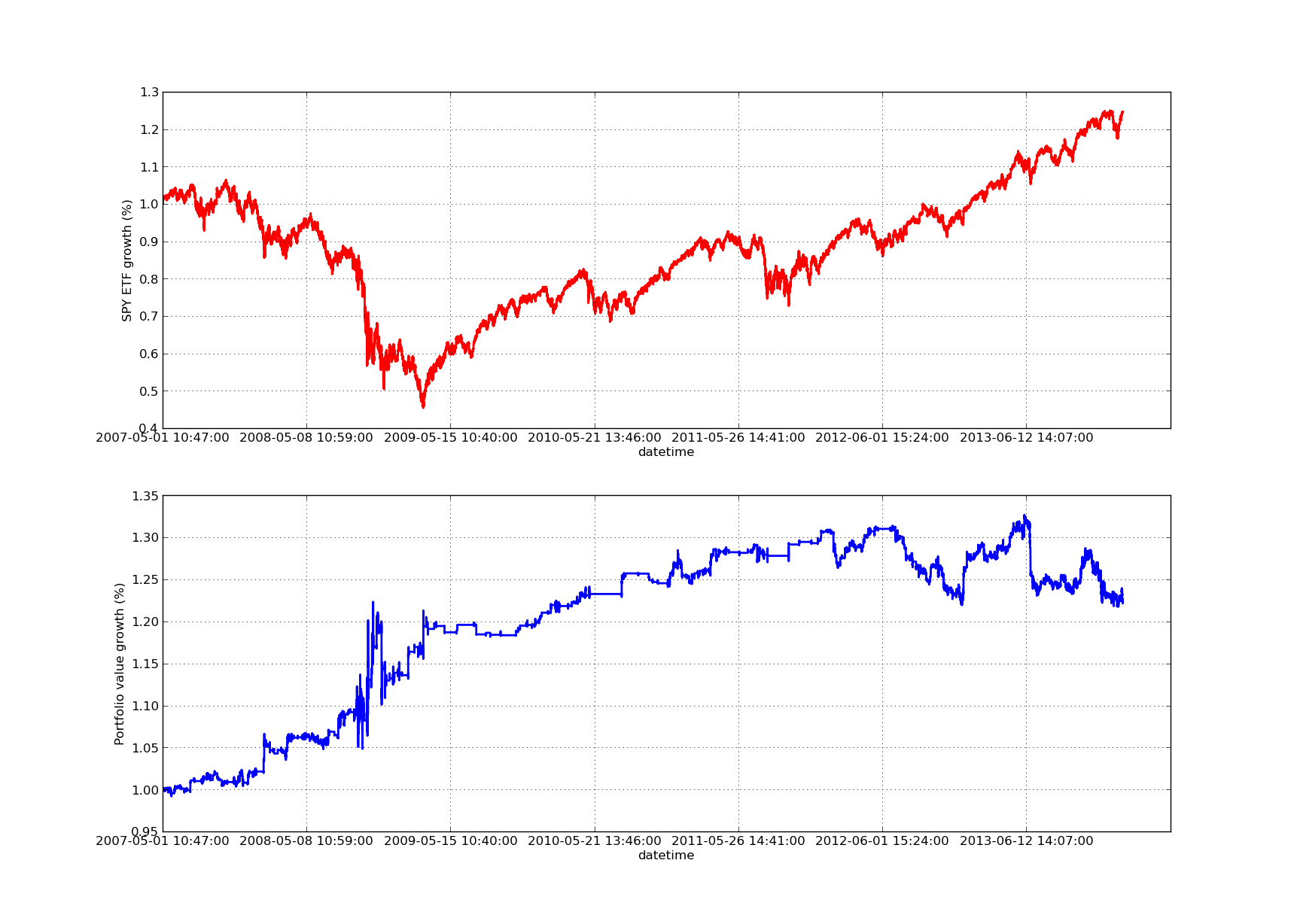
Анализ чувствительности коэффициента хеджирования линейной регрессии SPY-IWM за период обратного просмотра

Обратите внимание, что сокращение SPY было довольно значительным в 2009 году во время финансового кризиса. На этом этапе стратегия также переживает бурный период. Также следует отметить, что за последний год показатели ухудшились из-за сильной динамики индекса SPY в этот период, отражающей динамику индекса S&P 500.

Обратите внимание, что нам по-прежнему необходимо учитывать «смещение прогноза» при расчете разброса z-оценки. При этом все эти расчеты производятся без транзакционных издержек. Если принять во внимание эти факторы, данная стратегия обречена на неудачу. Размеры комиссий и проскальзывания в настоящее время не определены. Кроме того, стратегия предполагает торговлю дробными единицами ETF, что также крайне нереалистично.

В будущей статье мы создадим более сложный событийно-управляемый бэктестер, который будет учитывать все вышеперечисленное, что даст нам больше уверенности в нашей кривой капитала и показателях эффективности.