کاپی رائٹ نوٹس: اگر اس مضمون کے کوڈ کو نقل کرنے کی ضرورت ہو تو براہ کرم اس کا ماخذ بتائیں ، اگر تجارتی استعمال کے لئے ، مقالہ تحریر کرنے کے لئے براہ کرم ذاتی خط یا مصنف سے رابطہ کریں ای میل [email protected]

1. تعارف

کوانٹم ٹرانزیکشن کے فوائد

کوانٹم ٹریڈنگ کا مطلب یہ ہے کہ اعلی درجے کی ریاضیاتی ماڈل کے بجائے انسانوں کی طرف سے بنایا جانے والا فیصلہ ، حکمت عملی تیار کرنے کے لئے کمپیوٹر ٹکنالوجی کا استعمال کرتے ہوئے جس میں بڑے پیمانے پر تاریخی اعداد و شمار سے سمندری انتخاب سے زیادہ منافع بخش ہونے کا امکان ہوتا ہے۔ اس سے سرمایہ کاروں کے جذبات میں اتار چڑھاؤ کے اثرات کو بہت حد تک کم کیا جاتا ہے ، جس سے مارکیٹ میں انتہائی جنون یا مایوسی کی صورت میں غیر منطقی سرمایہ کاری کے فیصلے سے بچا جاسکتا ہے۔ ڈیجیٹل کرنسی کی وجہ سے 24*ڈیجیٹل کرنسی کی مارکیٹ میں شروع ہونے سے ، یہ واضح طور پر ایک اچھی شروعات ہے۔ اس وقت ڈیجیٹل کرنسی کی مارکیٹ ابھی بھی ناتجربہ کار ہے۔ پلیٹ فارم ٹریڈنگ سسٹم میں خرابی ، کے لائن پلگ ان اب بھی کبھی کبھار ظاہر ہوتا ہے ، اور یہ مقدار کی تجارت کے لئے بھی ایک خطرہ ہے۔ تاہم ، ڈیجیٹل کرنسی میں مقدار کی تجارت کے لئے مجموعی طور پر فائدہ سے زیادہ نقصان ہے۔ کیونکہ ماڈل کی جانچ پڑتال اور ٹریننگ ٹائم سیریز کی جانچ پڑتال کے ذریعے ، ہم سب سے کم وقت میں سیکڑوں ماڈلوں میں بہترین موزوں طریقہ آزما سکتے ہیں۔

GQNR ماڈل کی وضاحت

         یہ ماڈل گارچ ماڈل پر مبنی ہے جس میں اتار چڑھاؤ کی پیشن گوئی کی گئی ہے۔ اس کے نتیجے میں عددی اعشاریہ کی واپسی کے ذریعہ اتار چڑھاؤ کی پیشن گوئی کی گئی ہے۔ اس کے بعد غیر لکیری واپسی کا استعمال کیا جاتا ہے ، جیسے کہ GA مستقبل میں اگلے دور میں اوپری VaR اور نچلے VaR کی پیشن گوئی کرنے کے لئے فولڈنگ کرتا ہے۔ اس طریقہ کار کو ماڈل کے طور پر مختصر طور پر GQNR کہا جاتا ہے۔

1. گارچ ماڈیول

اس سیکشن میں حکمت عملی گارچ کے بنیادی نکات کی تفصیل دی جائے گی ، جو مالیاتی منڈیوں میں کچھ حد تک عام ہے اور ڈیجیٹل کرنسیوں میں کچھ حد تک پیش گوئی کرنے والا اثر حاصل کرسکتا ہے۔

1.1 گارچ تعریف

آرچ ماڈل کا جوہر یہ ہے کہ بقایا مربع ترتیب کا استعمال کرتے ہوئے کیو درجے کی متحرک پلینٹ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ فاریکس ٹریڈنگ کے فوائد کیا ہیں؟ موجودہ فاریکس کے فوائد کے لئے فاریکس ٹریڈنگ کے فوائد؟ فاریکس ٹریڈنگ کے فوائد؟ فاریکس ٹریڈنگ کے فوائد اور نقصانات کے لئے فاریکس ٹریڈنگ کے فوائد اور نقصانات کے لئے فاریکس ٹریڈنگ کے فوائد اور نقصانات کے لئے فاریکس ٹریڈنگ کے فوائد اور نقصانات کے لئے فاریکس ٹریڈنگ کے فوائد؟          لیکن عملی طور پر ، کچھ بقایا سیریز کے اختیاری افعال طویل عرصے سے خود مختار ہیں ، جب ARCH ماڈل فٹ ہونے والے اختیاری افعال کا استعمال کرتے ہیں تو ، اس سے اعلی منتقل اوسط درجے پیدا ہوں گے ، جس سے پیرامیٹرز کا اندازہ لگانا مشکل ہوجائے گا اور آخر کار ARCH ماڈل کی فٹ ہونے کی درستگی کو متاثر کرے گا۔                                                                                       GARCH ماڈل دراصل ARCH کی بنیاد پر ہے ، جس میں فرق کے افعال کو مدنظر رکھتے ہوئے p درجے کی خود اعتمادی پیدا ہوتی ہے ، جو طویل مدتی یادداشت والے فرق کے افعال کو مؤثر طریقے سے فٹ کر سکتی ہے۔ ARCH ماڈل GARCH ماڈل کا ایک خاص مثال ہے ، P = 0 کے GARCH ((p ، q) ماڈل) ۔

1.2 ARCH عمل

        کی تعریف کی گئی ہے کہ اگر σn تجارت کے n ویں دور میں اثاثوں کے اتار چڑھاؤ کا اندازہ لگاتا ہے ، اور mu روزانہ کی واپسی کی شرح ہے ، تو اس کی بنیاد پر ایک غیر جانبدار اندازہ لگایا جاسکتا ہے واپسی کی شرح حالیہ m تجارتی دوروں میں: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         مندرجہ ذیل تبدیلیاں کریں 1μn-i کو فیصد منافع میں تبدیل کریں 2m-1 کو m میں تبدیل کریں 3 فرض کریں کہ μ = 0 ہے ، اور ان تبدیلیوں کا نتیجہ پر زیادہ اثر نہیں پڑتا ہے۔ مندرجہ بالا فارمولے کے مطابق ، اتار چڑھاؤ کی شرح کو آسان بنایا جاسکتا ہے: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(          یہ ہے کہ ہر دور میں اتار چڑھاؤ کی شرح کا مربع مساوی وزن 1 / m ہے ، کیونکہ یہ موجودہ اتار چڑھاؤ کا اندازہ ہے ، قریب کے اعداد و شمار کو زیادہ وزن دیا جانا چاہئے ، اس طرح اس کو تبدیل کیا جاسکتا ہے: \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi چوتھے تجارتی دور کے لئے منافع کی شرح کے مربع کا ایک فیکٹر ہے ، مثبت قدر لے لو اور i کی چھوٹی قدر جتنی بڑی ہے ، وزن کا مجموعہ 1 ہے۔ مزید توسیع ، فرض کریں کہ ایک طویل مدتی تناسب VL موجود ہے ، اور اس کا وزن وزن ہے ، مندرجہ بالا حساب سے حاصل کیا جاسکتا ہے:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        تاکہω = γVL ، فارمولہ (((15) میں تبدیل کیا جاسکتا ہے: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\( ہم عام ARCH () 1) عمل کو حاصل کر سکتے ہیں \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 GARCH عمل

          GARCH(p,q) ماڈل ARCH(p) اور EWMA(q) ماڈل کا ایک مجموعہ ہے ، جس کا مطلب یہ ہے کہ اتار چڑھاؤ کی شرح نہ صرف پچھلے پی کی آمدنی سے متعلق ہے ، بلکہ خود پہلے کیو کی مدت سے بھی متعلق ہے ، اس طرح بیان کیا گیا ہے: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         مندرجہ بالا فارمولے کے مطابق ہم عام طور پر حاصل کر سکتے ہیں GARCH(1,1): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 QR ماڈیولز

         اس سیکشن میں بنیادی عددی اعشاریہ کی واپسی کی وضاحت کی جائے گی ، جس میں اسٹریٹجک عددی اعشاریہ کی اہمیت کی وضاحت کی جائے گی

2.1 QR کی تعریف

عددی واپسی عددی واپسی متغیر X اور متغیر Y کے عددی عددی کے درمیان لکیری تعلقات کا اندازہ لگانے کا ایک طریقہ ہے۔ پچھلے رجعت ماڈل دراصل متغیرات کی وضاحت کی شرائط کی توقعات پر مبنی ہیں۔ اور لوگوں کو یہ بھی فکر ہے کہ متغیرات کی وضاحت کس طرح متغیرات کی تقسیم کے درمیانے درجے سے متعلق ہے۔ یہ سب سے پہلے کوئنکر اور باسسیٹ نے 1978 میں تجویز کیا تھا۔ OLS رجعت کا تخمینہ کم سے کم معذوری کے مربع پر مبنی ہے۔ عددی رجعت کا تخمینہ بھی ایک غیر متضاد شکل پر مبنی ہے۔ جس میں ، درمیانے درجے کی واپسی کم سے کم مطلق انحراف تخمینہ استعمال کرتی ہے۔

2.2 OLS سے QR تک

         عام رجعت کا طریقہ کم سے کم بائنری ضرب ہے ، یعنی کم سے کم غلطی کا مربع مجموعہ: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         اور عددی ہندسوں کا مقصد یہ ہے کہ مندرجہ بالا فارمولے کی بنیاد پر کم سے کم وزن کی غلطی کی مطلق قیمت اور: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 کیو آر کی نمائش

آپ دیکھ سکتے ہیں کہ تمام نمونوں کو الگ الگ جگہوں میں تقسیم کیا گیا ہے، اور یہ الگ الگ جگہوں میں تقسیم کیا گیا ہے، اور یہ الگ الگ جگہوں میں تقسیم کیا گیا ہے

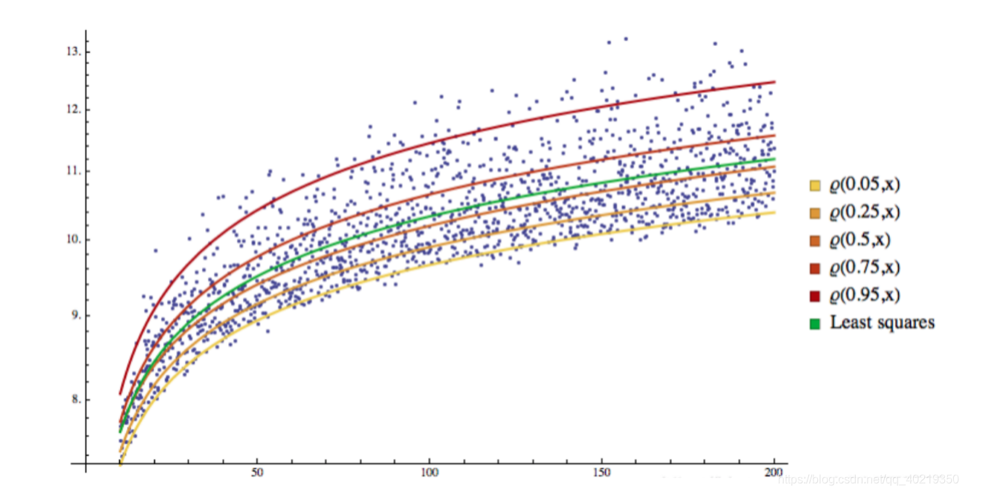
3. GARCH-QR واپسی

3.1 اتار چڑھاو کی شرح اور VaR کی واپسی کی شکل کا انتخاب

اس کے علاوہ ، یہ بھی کہا گیا ہے کہ اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے ، اس طرح کی حکمت عملی کے بارے میں بات کرنے کے لئے. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 ہدف کی تقریب کا تعین

        مندرجہ بالا معلومات کی بنیاد پر ، ہم مجموعہ کے بعد حتمی طور پر بہتر بنانے کے لئے ہدف کے افعال حاصل کرسکتے ہیں: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 مشین لرننگ کا استعمال کرتے ہوئے ہدف فنکشن کو بہتر بنانا

اس مرحلے میں زیادہ اختیارات ہیں ، روایتی درجے میں کمی ، اور جینیاتی الگورتھم بھی ، قارئین کو اپنی تخلیقی صلاحیتوں کو استعمال کرنے کے لئے استعمال کیا جاسکتا ہے۔ یہاں ، ہم نے ایک بہتر GA الگورتھم کا استعمال کیا ہے ، جس کے بارے میں ہمارے اپنے بلاگ میں تفصیل سے بتایا گیا ہے۔GA الگورتھم کے بارے میں پتہ

GQNR کو کس طرح استعمال کیا جائے؟

1۔ سوچ کا تعین

         جی کیو این آر کا بنیادی مرکز مارکیٹ میں اتار چڑھاؤ ہے ، ہر موجودہ وقت کے نقطہ پر ، اگلے دور میں اتار چڑھاؤ کی پیش گوئی کرنے کے لئے گارچ کے ذریعہ پیش گوئی کی جاسکتی ہے ، دوسری طرف ، ماضی کے اعداد و شمار کی پیش گوئی کرنے والے اتار چڑھاؤ کے اعشاریہ واپسی کے ذریعہ ، اتار چڑھاؤ کی کم قیمت حاصل کی جاسکتی ہے جو زیادہ تر ممکنہ حد سے تجاوز نہیں کرے گی۔ اوپری اور نچلی حد۔ اور یہ دونوں سرحدیں ، مجموعی طور پر بنیادی ہیں۔ جب اوپری سرحد کو ٹرگر کیا جاتا ہے تو ، ہم یہ سمجھ سکتے ہیں کہ مختصر مدت میں زیادہ تر ممکنہ حد سے نیچے جانے کا رجحان ہوگا ، اور جب نیچے کی حد کو ٹرگر کیا جاتا ہے تو ، ہم یہ سمجھ سکتے ہیں کہ مختصر مدت میں زیادہ تر ممکنہ حد سے اوپر جانے کا رجحان ہوگا۔

استعمال میں دشواری

• واپسی کی شکل میں
• موافقت پذیر الگورتھم کا انتخاب
• مشین سیکھنے کے لئے مناسب پیرامیٹرز
• مارکیٹ کی غیر یقینی اور بے ترتیب

3. حل

• حکمت عملی سیکھنے کے وقت کو کم کریں
• طویل مدتی خطرے کے خلاف کم سے کم جمع شدہ ضمانتیں
• ڈبل مساوی رجحانات کی مشترکہ توثیق میں اضافہ اور ثانوی قدر میں کمی کی تصدیق