جوڑوں کی تجارت ریاضی کے تجزیے پر مبنی تجارتی حکمت عملی تیار کرنے کی ایک بہترین مثال ہے، اس مضمون میں، ہم یہ ظاہر کریں گے کہ جوڑوں کی تجارت کی حکمت عملی بنانے اور خودکار کرنے کے لیے ڈیٹا کا فائدہ کیسے اٹھایا جائے۔

بنیادی اصول

فرض کریں کہ آپ کے پاس سرمایہ کاری کا ایک جوڑا X اور Y ہے جس کا کچھ بنیادی تعلق ہے، جیسے کہ دونوں کمپنیاں ایک ہی مصنوعات تیار کرتی ہیں، جیسے Pepsi اور Coca-Cola۔ آپ چاہتے ہیں کہ دونوں کے درمیان قیمت کا تناسب یا بنیاد (اسپریڈ بھی کہا جاتا ہے) وقت کے ساتھ ساتھ مستقل رہے۔ تاہم، وقتاً فوقتاً سپلائی اور ڈیمانڈ کی تبدیلیوں کی وجہ سے دو جوڑوں کے درمیان پھیلاؤ مختلف ہو سکتا ہے، جیسے کہ ایک سرمایہ کاری کے ہدف کے لیے بڑے خرید/فروخت کے آرڈر، کسی ایک کمپنی کے بارے میں اہم خبروں پر ردعمل وغیرہ۔ اس صورت میں، ایک سرمایہ کاری اوپر کی طرف اور دوسری ایک دوسرے کے مقابلے میں نیچے کی طرف بڑھ جاتی ہے۔ اگر آپ توقع کرتے ہیں کہ وقت گزرنے کے ساتھ یہ انحراف معمول پر آجائے گا، تو آپ تجارتی موقع (یا ثالثی کا موقع) دیکھ سکتے ہیں۔ اس طرح کے ثالثی کے مواقع ڈیجیٹل کرنسی مارکیٹ یا گھریلو کموڈٹی فیوچر مارکیٹ میں ہر جگہ موجود ہیں، جیسے کہ بی ٹی سی اور محفوظ پناہ گاہوں کے درمیان تعلق؛ سویا بین کے کھانے، سویا بین کے تیل اور مستقبل میں سویا بین کی اقسام کے درمیان تعلق۔

جب قیمت میں کوئی عارضی فرق ہوتا ہے، تو تجارت بہتر کارکردگی کا مظاہرہ کرنے والی سرمایہ کاری کو فروخت کرے گی اور کم کارکردگی والی سرمایہ کاری کو خریدے گی (وہ سرمایہ کاری جو گر گئی ہے) اسپریڈ کی عکاسی آخر کار بہتر کارکردگی والی سرمایہ کاری کے پیچھے پڑنے سے ہوگی یا کم کارکردگی کا مظاہرہ کرنے والی سرمایہ کاری کے پیچھے بڑھنے سے، یا آپ کی تجارت ان تمام منظرناموں میں پیسہ کمائے گی۔ اگر سرمایہ کاری ان کے درمیان فرق کو تبدیل کیے بغیر ایک ساتھ اوپر یا نیچے منتقل ہوتی ہے، تو آپ پیسہ کمائیں گے یا کھویں گے۔

لہذا، جوڑوں کی تجارت ایک مارکیٹ کی غیر جانبدار تجارتی حکمت عملی ہے جو تاجروں کو مارکیٹ کی تقریباً کسی بھی حالت سے فائدہ اٹھانے کے قابل بناتی ہے: اوپر کا رجحان، نیچے کا رجحان یا سائیڈ ویز۔

تصور کی وضاحت کریں: دو فرضی سرمایہ کاری کے اہداف

• موجد مقداری پلیٹ فارم پر اپنے تحقیقی ماحول کی تعمیر

سب سے پہلے، ہموار طریقے سے کام کرنے کے لیے، ہمیں اپنے تحقیقی ماحول کو بنانے کی ضرورت ہے، اس مضمون میں، ہم تحقیقی ماحول کو بنانے کے لیے Inventor Quantitative Platform (FMZ.COM) کا استعمال کرتے ہیں، بنیادی طور پر تاکہ ہم آسان اور تیز API کا استعمال کر سکیں۔ بعد میں اس پلیٹ فارم کا انٹرفیس اور انکیپسولیشن مکمل ڈوکر سسٹم۔

موجد کوانٹیٹیو پلیٹ فارم کے آفیشل نام پر، اس ڈوکر سسٹم کو میزبان سسٹم کہا جاتا ہے۔

میزبانوں اور روبوٹس کو تعینات کرنے کے طریقے کے بارے میں مزید معلومات کے لیے، براہ کرم میرا سابقہ ​​مضمون دیکھیں: https://www.fmz.com/bbs-topic/4140

وہ قارئین جو اپنا کلاؤڈ کمپیوٹنگ سرور تعیناتی میزبان خریدنا چاہتے ہیں اس مضمون کا حوالہ دے سکتے ہیں: https://www.fmz.com/bbs-topic/2848

کلاؤڈ کمپیوٹنگ سروس اور ہوسٹ سسٹم کو کامیابی کے ساتھ تعینات کرنے کے بعد، ہم سب سے طاقتور Python ٹول انسٹال کریں گے: ایناکونڈا

اس مضمون کے لیے درکار تمام متعلقہ پروگرام ماحول کو حاصل کرنے کے لیے (انحصار لائبریریاں، ورژن کا انتظام، وغیرہ)، سب سے آسان طریقہ ایناکونڈا کا استعمال ہے۔ یہ ایک پیکڈ Python ڈیٹا سائنس ایکو سسٹم اور انحصار مینیجر ہے۔

ایناکونڈا کی تنصیب کے طریقہ کار کے لیے، براہ کرم ایناکونڈا کے آفیشل گائیڈ سے رجوع کریں: https://www.anaconda.com/distribution/

اس مضمون میں Python سائنسی کمپیوٹنگ میں دو بہت مشہور اور اہم لائبریریوں Numpy اور pandas کا بھی استعمال کیا جائے گا۔

مندرجہ بالا بنیادی کام کے لیے، آپ میرے پچھلے مضمون کو بھی دیکھ سکتے ہیں، جس میں بتایا گیا ہے کہ ایناکونڈا ماحول اور دو لائبریریوں کو کیسے ترتیب دیا جائے، تفصیلات کے لیے، براہ کرم دیکھیں: https://www.fmz.com/digest-۔ موضوع/4169

اگلا، آئیے “دو فرضی سرمایہ کاری کے اہداف” کو نافذ کرنے کے لیے کوڈ کا استعمال کریں

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

جی ہاں، ہم matplotlib بھی استعمال کریں گے، Python میں ایک بہت مشہور چارٹ لائبریری۔

آئیے ایک فرضی سرمایہ کاری کا اثاثہ X بنائیں اور ایک عام تقسیم کا استعمال کرتے ہوئے اس کے یومیہ منافع کی منصوبہ بندی کریں۔ اس کے بعد ہم روزانہ X قدر حاصل کرنے کے لیے ایک مجموعی رقم انجام دیتے ہیں۔

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

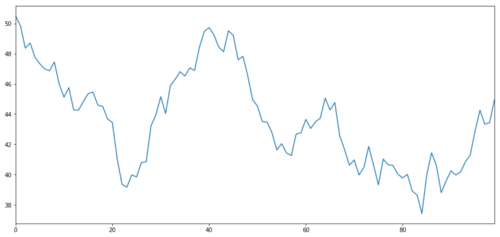
سرمایہ کاری کا ہدف X، اس کی روزانہ کی واپسی کو معمول کی تقسیم کے ذریعے نقل کریں اور کھینچیں۔

اب ہم Y پیدا کرتے ہیں جو X کے ساتھ مضبوطی سے جڑا ہوا ہے، لہذا Y کی قیمت کو X میں ہونے والی تبدیلیوں سے بالکل اسی طرح منتقل ہونا چاہیے۔ ہم X لے کر، اسے اوپر منتقل کر کے، اور عام تقسیم سے اخذ کردہ کچھ بے ترتیب شور کو شامل کر کے اس کا نمونہ بناتے ہیں۔

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

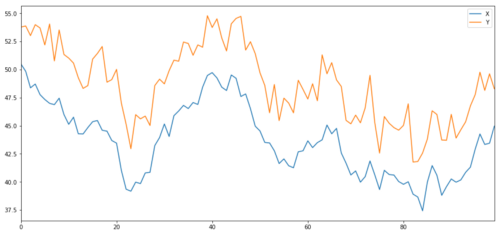
سرمایہ کاری کے اہداف X اور Y کو مربوط کرنا

ہم آہنگی

ہم آہنگی باہمی تعلق سے بہت ملتی جلتی ہے، مطلب یہ ہے کہ دو اعداد و شمار کی سیریز کا تناسب اوسط کے ارد گرد مختلف ہوگا:

Y = ⍺ X + e

جہاں ⍺ ایک مستقل تناسب ہے اور e شور ہے۔

دو وقتی سیریز کے درمیان تجارتی جوڑے کے لیے، وقت کے ساتھ تناسب کی متوقع قدر کو وسط میں تبدیل ہونا چاہیے، یعنی ان کو مربوط کیا جانا چاہیے۔ ہم نے اوپر جو ٹائم سیریز بنائی ہے وہ مربوط ہیں۔ اب ہم دونوں کے درمیان پیمانہ کھینچیں گے تاکہ ہم دیکھ سکیں کہ یہ کیسا نظر آئے گا۔

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

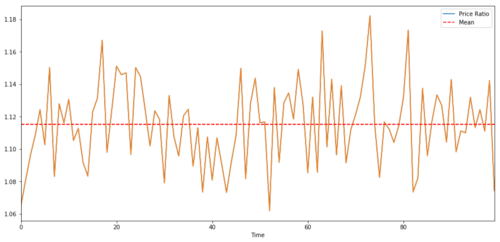
دو مربوط سرمایہ کاری کی قیمتوں کا تناسب اور اوسط

ہم آہنگی ٹیسٹ

اس کی جانچ کرنے کا ایک آسان طریقہ statsmodels.tsa.stattools استعمال کرنا ہے۔ ہمیں ایک بہت کم p-value دیکھنا چاہئے کیونکہ ہم نے مصنوعی طور پر دو ڈیٹا سیریز بنائی ہیں جو ممکن حد تک مربوط ہیں۔

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

نتیجہ ہے: 1.81864477307e-17

نوٹ: ارتباط اور ہم آہنگی

اگرچہ ارتباط اور ہم آہنگی نظریہ میں ایک جیسے ہیں، لیکن وہ ایک جیسے نہیں ہیں۔ آئیے ڈیٹا سیریز کی مثالیں دیکھتے ہیں جو باہم مربوط ہیں لیکن مربوط نہیں ہیں، اور اس کے برعکس۔ پہلے آئیے اس سیریز کے ارتباط کو چیک کرتے ہیں جو ہم نے ابھی تیار کیا ہے۔

X.corr(Y)

نتیجہ ہے: 0.951

جیسا کہ ہم نے توقع کی تھی، یہ بہت زیادہ ہے۔ لیکن ان دو سیریزوں کا کیا ہوگا جو باہم مربوط ہیں لیکن مربوط نہیں ہیں؟ ایک سادہ مثال دو ڈیٹا سیریز ہے جو مختلف ہوتی ہیں۔

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

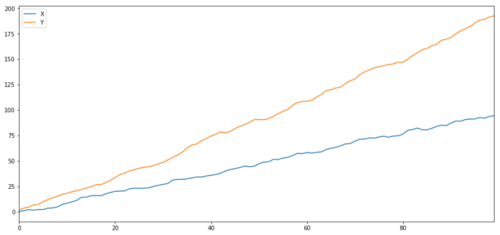
دو متعلقہ سیریز (مشترکہ نہیں)

ارتباط کا گتانک: 0.998 کوانٹیگریشن ٹیسٹ پی ویلیو: 0.258

باہمی ربط کے بغیر ہم آہنگی کی سادہ مثالیں عام طور پر تقسیم شدہ سیریز اور مربع لہر ہیں۔

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()

Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

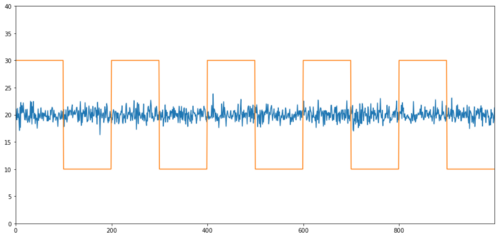
ارتباط: 0.007546 کوانٹیگریشن ٹیسٹ پی ویلیو: 0.0

ارتباط بہت کم ہے، لیکن p-value کامل ہم آہنگی کو ظاہر کرتا ہے!

جوڑوں کی تجارت کیسے کی جائے؟

چونکہ دو مربوط ٹائم سیریز (جیسے اوپر X اور Y) ایک دوسرے کی طرف اور دور ہوتے ہیں، ایسے اوقات ہوتے ہیں جب ایک اعلی بنیاد اور ایک کم بنیاد ہوتی ہے۔ ہم ایک سرمایہ کاری خرید کر اور دوسری فروخت کر کے جوڑے کی تجارت کرتے ہیں۔ اس طرح، اگر سرمایہ کاری کے دو اہداف ایک ساتھ گرتے ہیں یا بڑھتے ہیں، تو ہم نہ تو پیسہ کماتے ہیں اور نہ ہی پیسہ کماتے ہیں، یعنی ہم مارکیٹ غیر جانبدار ہیں۔

اوپر والے Y = ⍺ X + e میں X اور Y پر واپس جائیں، ہم تناسب (Y/X) کو اس کے اوسط ⍺ کے گرد گھومتے ہوئے پیسہ کماتے ہیں، ایسا کرنے کے لیے، ہم نوٹ کرتے ہیں کہ جب X ⍺ کی قدر بھی ہوتی ہے۔ زیادہ یا بہت کم، ⍺ کی قدر بہت زیادہ یا بہت کم ہے:

• لمبا تناسب: یہ تب ہوتا ہے جب تناسب ⍺ چھوٹا ہوتا ہے اور ہم اس کے بڑے ہونے کی توقع کرتے ہیں۔ اوپر کی مثال میں، ہم لمبا Y اور مختصر X جا کر پوزیشن کھولتے ہیں۔

• مختصر تناسب: یہ تب ہوتا ہے جب تناسب ⍺ بڑا ہوتا ہے اور ہم اس کے چھوٹے ہونے کی توقع کرتے ہیں۔ اوپر کی مثال میں، ہم Y کو مختصر کرکے اور X کو لمبا کرکے پوزیشن کھولتے ہیں۔

نوٹ کریں کہ ہمارے پاس ہمیشہ ایک “ہیجڈ پوزیشن” ہوتی ہے: اگر بنیادی لمبی قیمت کھو دیتی ہے، تو مختصر پوزیشن پیسہ کماتی ہے، اور اس کے برعکس، اس لیے ہم مارکیٹ کی مجموعی نقل و حرکت سے محفوظ ہیں۔

جیسا کہ اثاثے X اور Y ایک دوسرے کے نسبت منتقل ہوتے ہیں، ہم پیسہ کماتے ہیں یا پیسہ کھو دیتے ہیں۔

اسی طرح کے رویے کے ساتھ لین دین تلاش کرنے کے لیے ڈیٹا کا استعمال کریں۔

ایسا کرنے کا بہترین طریقہ یہ ہے کہ ان تجارتوں کے ساتھ شروع کریں جن کے بارے میں آپ کو شبہ ہے کہ آپس میں مربوط ہو سکتے ہیں اور شماریاتی ٹیسٹ کریں۔ اگر آپ تمام تجارتی جوڑوں پر شماریاتی ٹیسٹ کرتے ہیں، تو آپ ہوں گے۔متعدد موازنہ تعصبکا شکار.

متعدد موازنہ تعصباس صورت حال سے مراد ہے جہاں بہت سے ٹیسٹ چلانے پر غلط طریقے سے اہم p-value پیدا کرنے کا امکان بڑھ جاتا ہے، کیونکہ ہمیں بڑی تعداد میں ٹیسٹ چلانے کی ضرورت ہے۔ اگر ہم اس ٹیسٹ کو بے ترتیب ڈیٹا پر 100 بار چلاتے ہیں، تو ہمیں 0.05 سے نیچے 5 p-values ​​دیکھنا چاہیے۔ اگر آپ انٹیگریشن کے لیے n آلات کا موازنہ کر رہے ہیں، تو آپ n(n-1)/2 موازنہ کر رہے ہوں گے اور آپ کو بہت سی غلط p-values ​​نظر آئیں گی، جو آپ کے ٹیسٹ کے نمونے کے سائز میں اضافے کے ساتھ بڑھیں گی۔ اس سے بچنے کے لیے، چند ایسے تجارتی جوڑے منتخب کریں جن کے بارے میں آپ کے پاس یقین کرنے کی وجہ ہے کہ ان کے آپس میں مربوط ہونے کا امکان ہے، اور پھر انفرادی طور پر ان کی جانچ کریں۔ اس سے کافی حد تک کمی آئے گی۔متعدد موازنہ تعصب。

تو آئیے کچھ آلات تلاش کرنے کی کوشش کرتے ہیں جو S&P 500 میں یو ایس لاج کیپ ٹیکنالوجی اسٹاکس کی ایک ٹوکری لیتے ہیں۔ ہم تجارتی آلات کی فہرست کو اسکین کرتے ہیں اور تمام جوڑوں کے درمیان ہم آہنگی کے لیے ٹیسٹ کرتے ہیں۔

واپس کیے گئے کوانٹیگریشن ٹیسٹ سکور میٹرکس، پی ویلیو میٹرکس، اور 0.05 سے کم پی ویلیو والے تمام جوڑے کے مطابق میچز شامل ہیں۔یہ طریقہ متعدد موازنہ تعصب کا شکار ہے، لہذا عملی طور پر انہیں دوسری توثیق کرنے کی ضرورت ہے۔ اس مضمون میں، ہماری وضاحت کی سہولت کے لیے، ہم مثالوں میں اسے نظر انداز کرنے کا انتخاب کرتے ہیں۔

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

نوٹ: ہم نے اپنے ڈیٹا میں مارکیٹ بینچ مارک (SPX) کو شامل کیا ہے - مارکیٹ بہت سے آلات کے بہاؤ کو چلاتی ہے اور اکثر آپ کو دو آلات مل سکتے ہیں جو ایک دوسرے کے ساتھ مربوط ہوتے ہیں لیکن درحقیقت وہ ایک دوسرے کے ساتھ مربوط نہیں ہوتے، بلکہ ان کے ساتھ ملتے ہیں۔ مارکیٹ اس کو الجھانے والا متغیر کہا جاتا ہے جو آپ کو ملتا ہے اس میں مارکیٹ کی شرکت کا جائزہ لینا ضروری ہے۔

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

اب ہم اپنے طریقے کو استعمال کرتے ہوئے مربوط تجارتی جوڑے تلاش کرنے کی کوشش کریں۔

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

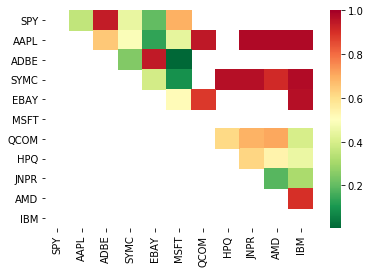
ایسا لگتا ہے کہ ‘ADBE’ اور ‘MSFT’ یکجا ہیں۔ آئیے اس بات کو یقینی بنانے کے لیے قیمت پر ایک نظر ڈالتے ہیں کہ یہ اصل میں معنی خیز ہے۔

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

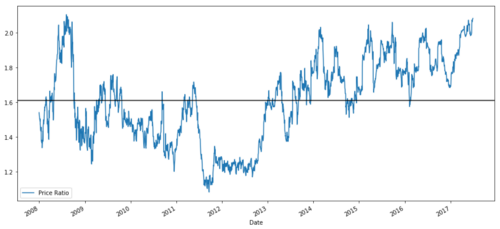
2008 سے 2017 تک MSFT اور ADBE کے درمیان قیمت کے تناسب کا چارٹ

یہ تناسب ایک مستحکم اوسط کی طرح لگتا ہے۔ مطلق تناسب اعدادوشمار کے لحاظ سے زیادہ مفید نہیں ہیں۔ ہمارے سگنل کو زیڈ سکور کے طور پر دیکھ کر اسے معمول پر لانا زیادہ مددگار ہے۔ Z سکور کی تعریف اس طرح کی گئی ہے:

Z Score (Value) = (Value — Mean) / Standard Deviation

خبردار کرنا

عملی طور پر، ہم عام طور پر ڈیٹا میں کچھ توسیع کا اطلاق کرنے کی کوشش کرتے ہیں، لیکن صرف اس صورت میں جب ڈیٹا کو عام طور پر تقسیم کیا جائے۔ تاہم، زیادہ مالیاتی ڈیٹا عام طور پر تقسیم نہیں کیا جاتا ہے، اس لیے ہمیں بہت محتاط رہنا چاہیے کہ اعداد و شمار تیار کرتے وقت صرف معمول یا کسی خاص تقسیم کو فرض نہ کریں۔ تناسب کی حقیقی تقسیم میں چکنائی کی دم ہو سکتی ہے، اور اعداد و شمار جو انتہا کی طرف ہوتے ہیں ہمارے ماڈل کو الجھ سکتے ہیں اور بہت زیادہ نقصانات کا باعث بن سکتے ہیں۔

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

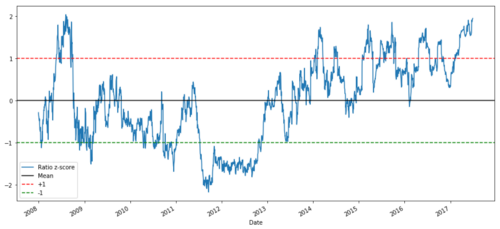
2008 سے 2017 تک MSFT اور ADBE کے درمیان Z- قیمت کا تناسب

اب یہ دیکھنا آسان ہے کہ تناسب کس طرح وسط کے گرد گھومتا ہے، لیکن بعض اوقات اس میں وسط سے بڑا انحراف ہوتا ہے، جس کا ہم فائدہ اٹھا سکتے ہیں۔

اب جب کہ ہم نے جوڑوں کی تجارت کی حکمت عملی کی بنیادی باتوں پر تبادلہ خیال کیا ہے اور قیمت کی تاریخ کی بنیاد پر ہم آہنگی کے اہداف کی نشاندہی کی ہے، آئیے ایک تجارتی سگنل تیار کرنے کی کوشش کرتے ہیں۔ سب سے پہلے، آئیے ڈیٹا تکنیک کا استعمال کرتے ہوئے تجارتی سگنل تیار کرنے کے اقدامات کا جائزہ لیں:

• قابل اعتماد ڈیٹا اکٹھا کرنا اور ڈیٹا کو صاف کرنا

• ٹریڈنگ سگنلز/منطق کی شناخت کے لیے ڈیٹا سے فنکشنز بنائیں

• خصوصیات حرکت پذیری اوسط یا قیمت کا ڈیٹا، زیادہ پیچیدہ سگنلز کے ارتباط یا تناسب ہو سکتی ہیں - نئی خصوصیات بنانے کے لیے ان کو یکجا کریں۔

• ٹریڈنگ سگنلز بنانے کے لیے ان خصوصیات کا استعمال کریں، یعنی کون سے سگنلز خرید، فروخت یا مختصر پوزیشن ہیں۔

خوش قسمتی سے، ہمارے پاس انوینٹر کوانٹیٹیو پلیٹ فارم (fmz.com) ہے جو ہمارے لیے حکمت عملی تیار کرنے والوں کے لیے ایک بہت بڑی نعمت ہے۔

انوینٹر کوانٹیٹیو پلیٹ فارم پر، مختلف مین اسٹریم ایکسچینجز کے پیکڈ انٹرفیسز ہیں، ہمیں صرف ان API انٹرفیسز کو کال کرنے کی ضرورت ہے جو کہ ایک پیشہ ور ٹیم کے ذریعہ تیار کی گئی ہے۔

اصولوں کی منطقی تکمیل اور وضاحت کے لیے، ہم ان بنیادی منطقوں کو تفصیلی انداز میں پیش کریں گے، لیکن اصل عمل میں، قارئین مندرجہ بالا چار پہلوؤں کو مکمل کرنے کے لیے براہ راست Inventor Quant کے API انٹرفیس کو کال کر سکتے ہیں۔

آئیے شروع کریں:

مرحلہ 1: اپنا مسئلہ ترتیب دیں۔

یہاں ہم ایک سگنل بنانے کی کوشش کر رہے ہیں جو ہمیں بتاتا ہے کہ آیا تناسب اگلے لمحے خرید یا فروخت ہو گا، جو ہمارا پیشن گوئی کرنے والا متغیر Y ہے:

Y = Ratio is buy (1) or sell (-1)

Y(t)= Sign(Ratio(t+1) — Ratio(t))

نوٹ کریں کہ ہمیں بنیادی اثاثہ کی اصل قیمت، یا یہاں تک کہ تناسب کی اصل قیمت (اگرچہ ہم کر سکتے ہیں) کی پیشن گوئی کرنے کی ضرورت نہیں ہے، ہمیں صرف اگلے تناسب کی سمت کی پیشن گوئی کرنے کی ضرورت ہے۔

مرحلہ 2: قابل اعتماد اور درست ڈیٹا اکٹھا کریں۔

موجد کوانٹ آپ کا دوست ہے! آپ صرف ان آلات کی وضاحت کرتے ہیں جن کی آپ تجارت کرنا چاہتے ہیں اور وہ ڈیٹا سورس جو آپ استعمال کرنا چاہتے ہیں، اور یہ مطلوبہ ڈیٹا نکالے گا اور اسے ڈیویڈنڈ اور انسٹرومنٹ اسپلٹ کے لیے صاف کرے گا۔ تو یہاں ہمارا ڈیٹا پہلے ہی بہت صاف ہے۔

ہم نے گزشتہ 10 سالوں میں تجارتی دنوں کے لیے Yahoo Finance سے درج ذیل ڈیٹا کا استعمال کیا (تقریباً 2,500 ڈیٹا پوائنٹس): کھلا، بند، بلند، کم، اور حجم

مرحلہ 3: ڈیٹا تقسیم کریں۔

اپنے ماڈل کی درستگی کو جانچنے کے اس اہم قدم کو مت بھولنا۔ ہم ڈیٹا کی درج ذیل ٹرین/توثیق/ٹیسٹ اسپلٹ استعمال کر رہے ہیں۔

• Training 7 years ~ 70%

• Test ~ 3 years 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

مثالی طور پر، ہم توثیق کا سیٹ بھی بنائیں گے، لیکن ہم ابھی ایسا نہیں کریں گے۔

مرحلہ 4: فیچر انجینئرنگ

متعلقہ افعال کیا ہو سکتے ہیں؟ ہم تناسب کی تبدیلی کی سمت کا اندازہ لگانا چاہتے ہیں۔ ہم نے دیکھا ہے کہ ہمارے دونوں آلات ایک ساتھ مربوط ہیں، اس لیے یہ تناسب بدل جائے گا اور وسط کی طرف لوٹ جائے گا۔ ایسا لگتا ہے کہ ہماری خصوصیت کو تناسب کے وسط کا کچھ پیمانہ ہونا چاہئے، اور موجودہ قدر اور اوسط کے درمیان فرق ہمارے تجارتی سگنل کو پیدا کر سکتا ہے۔

ہم مندرجہ ذیل افعال استعمال کرتے ہیں:

• 60 دن کی حرکت کا اوسط تناسب: رولنگ اوسط کا ایک پیمانہ

• 5 دن کی حرکت کا اوسط تناسب: اوسط کی موجودہ قیمت کا ایک پیمانہ

• 60 دن کا معیاری انحراف

• z-score: (5d MA - 60d MA) / 60d SD

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

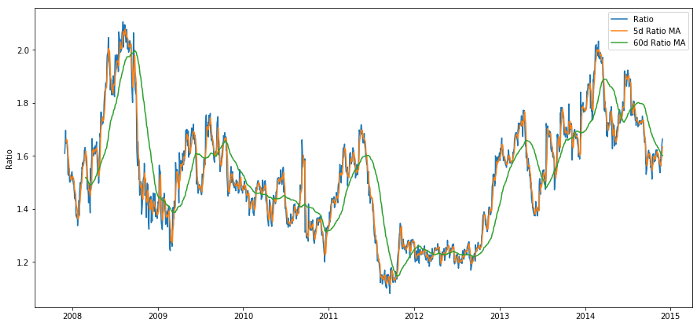
قیمت کا تناسب 60d اور 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

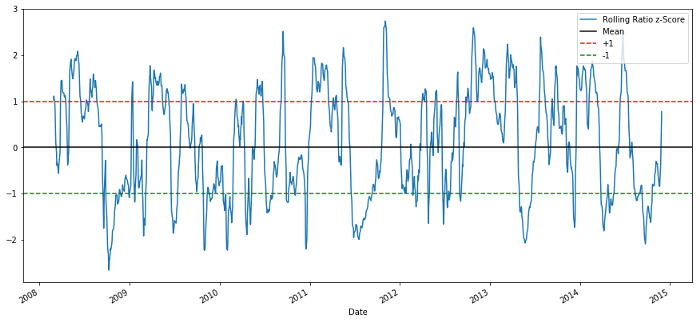
60-5 زیڈ اسکور قیمت کا تناسب

رولنگ میین کا زیڈ اسکور واقعی تناسب کی اوسط کو واپس لانے والی نوعیت کو ظاہر کرتا ہے!

مرحلہ 5: ماڈل کا انتخاب

آئیے ایک بہت ہی آسان ماڈل کے ساتھ شروع کریں۔ زیڈ سکور گراف کو دیکھتے ہوئے، ہم دیکھ سکتے ہیں کہ جب بھی زیڈ سکور بہت زیادہ یا بہت کم ہوتا ہے، یہ پیچھے ہٹ جاتا ہے۔ آئیے بہت زیادہ اور بہت کم کی وضاحت کرنے کے لیے اپنی حد کے طور پر +1/-1 کا استعمال کریں، پھر ہم ٹریڈنگ سگنلز بنانے کے لیے درج ذیل ماڈل کا استعمال کر سکتے ہیں:

• جب z -1.0 سے نیچے ہو تو تناسب خریدا جاتا ہے (1) کیونکہ ہم توقع کرتے ہیں کہ z 0 پر واپس آجائے گا، اس لیے تناسب بڑھ جاتا ہے۔

• جب z 1.0 سے اوپر ہوتا ہے تو تناسب فروخت ہوتا ہے (-1) کیونکہ ہم z کے 0 پر واپس آنے کی توقع کرتے ہیں، اس طرح تناسب کم ہو جاتا ہے۔

مرحلہ 6: تربیت، توثیق، اور اصلاح

آخر میں، آئیے دیکھتے ہیں کہ ہمارے ماڈل کا حقیقی ڈیٹا پر کیا اثر ہوتا ہے؟ آئیے دیکھتے ہیں کہ یہ سگنل حقیقی تناسب میں کیسے برتاؤ کرتا ہے۔

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

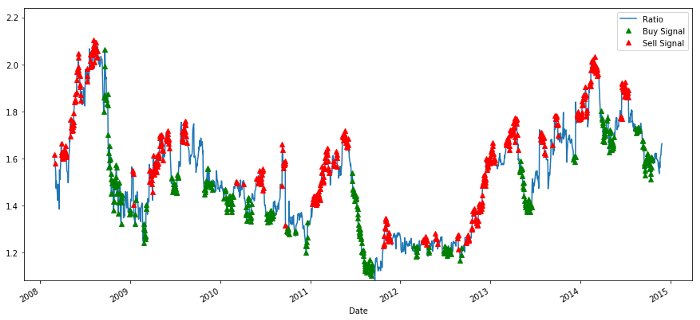
خرید و فروخت قیمت کے تناسب کے سگنل

یہ سگنل معقول معلوم ہوتا ہے، ایسا لگتا ہے کہ ہم تناسب کو بیچتے ہیں جب یہ زیادہ ہو یا بڑھتا ہو (سرخ نقطے) اور جب یہ کم ہو (سبز نقطے) اور کم ہو تو اسے واپس خریدیں۔ ہمارے لین دین کے اصل موضوع کے لیے اس کا کیا مطلب ہے؟ آئیے دیکھتے ہیں

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

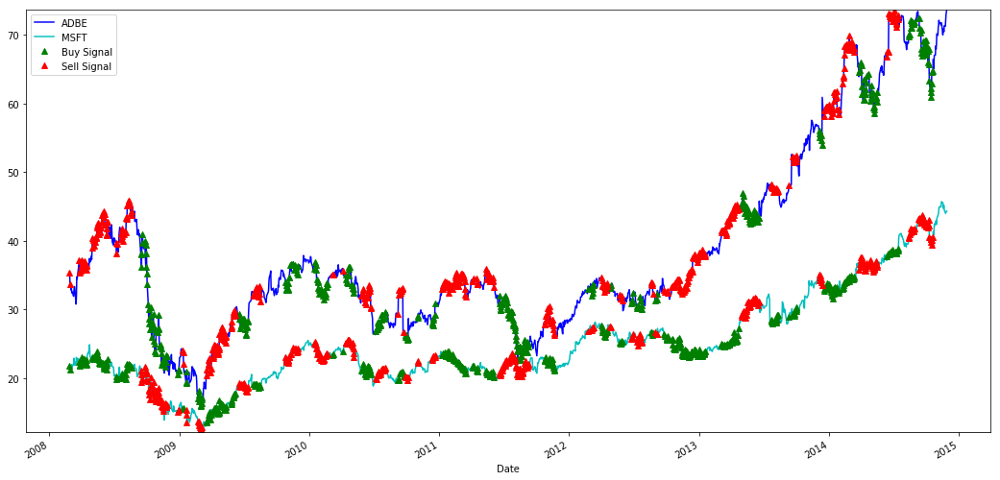
MSFT اور ADBE اسٹاکس کی خرید و فروخت کے اشارے

غور کریں کہ ہم کبھی کبھار “شارٹ ٹانگ”، کبھی “لمبی ٹانگ” اور کبھی دونوں پر پیسہ کیسے کماتے ہیں۔

ہم تربیت کے اعداد و شمار کے سگنل سے خوش ہیں۔ آئیے دیکھتے ہیں کہ یہ سگنل کس قسم کا منافع پیدا کر سکتا ہے۔ ہم ایک سادہ بیکٹیسٹر بنا سکتے ہیں جو تناسب کم ہونے پر 1 تناسب خریدتا ہے (1 ADBE اسٹاک خریدتا ہے اور تناسب x MSFT اسٹاک فروخت کرتا ہے) اور 1 تناسب فروخت کرتا ہے (1 ADBE اسٹاک اور کال ریشو x MSFT اسٹاک فروخت کرتا ہے) اور ان کے لیے PnL تجارت کا حساب لگا سکتے ہیں۔ تناسب

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

نتیجہ ہے: 1783.375

تو یہ حکمت عملی منافع بخش معلوم ہوتی ہے! اب، ہم موونگ ایوریج ٹائم ونڈو کو تبدیل کر کے، خرید/فروخت اور قریبی پوزیشنز وغیرہ کے لیے حد کو تبدیل کر کے مزید بہتر کر سکتے ہیں اور توثیق کے ڈیٹا پر کارکردگی میں بہتری کو چیک کر سکتے ہیں۔

ہم 1/-1 پیشین گوئیوں کے لیے مزید پیچیدہ ماڈلز جیسے لاجسٹک ریگریشن، SVM وغیرہ کو بھی آزما سکتے ہیں۔

اب، آئیے اس ماڈل کو آگے بڑھاتے ہیں، جو ہمیں لاتا ہے۔

مرحلہ 7: ٹیسٹ ڈیٹا کا بیک ٹیسٹ کریں۔

یہاں میں انوینٹر کوانٹیٹیو پلیٹ فارم کا ذکر کرنا چاہوں گا یہ تاریخی ماحول کو صحیح معنوں میں دوبارہ پیش کرنے، عام مقداری بیک ٹیسٹنگ ٹریپس کو ختم کرنے اور حکمت عملی کی خامیوں کو فوری طور پر دریافت کرنے کے لیے ایک اعلیٰ کارکردگی کا حامل QPS/TPS بیک ٹیسٹنگ انجن استعمال کرتا ہے، تاکہ بہتر طریقے سے حقیقی معلومات فراہم کی جا سکیں۔ - وقت کی سرمایہ کاری کی مدد۔

اصول کی وضاحت کے لیے، یہ مضمون عملی اطلاق میں، یہ تجویز کیا جاتا ہے کہ قارئین وقت کی بچت کے علاوہ، غلطی برداشت کرنے کی شرح کو بہتر بنائیں۔

بیک ٹیسٹنگ آسان ہے ہم ٹیسٹ ڈیٹا کے PnL کو دیکھنے کے لیے اوپر کا فنکشن استعمال کر سکتے ہیں۔

trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)

نتیجہ ہے: 5262.868

یہ ماڈل بہت اچھی طرح سے کیا گیا ہے! یہ ہمارا پہلا سادہ جوڑا ٹریڈنگ ماڈل بن گیا۔

اوور فٹنگ سے پرہیز کریں۔

اس سے پہلے کہ میں ختم کروں، میں خاص طور پر اوور فٹنگ کے بارے میں بات کرنا چاہوں گا۔ تجارتی حکمت عملیوں میں اوور فٹنگ سب سے خطرناک خرابی ہے۔ ایک اوور فٹنگ الگورتھم بیک ٹیسٹنگ میں بہت اچھی کارکردگی کا مظاہرہ کر سکتا ہے لیکن نئے ان دیکھے ڈیٹا پر ناکام ہو سکتا ہے - یعنی یہ واقعی ڈیٹا میں کسی رجحان کو ظاہر نہیں کرتا ہے اور اس میں کوئی حقیقی پیشین گوئی کی طاقت نہیں ہے۔ آئیے ایک سادہ سی مثال لیتے ہیں۔

ہمارے ماڈل میں، ہم رولنگ پیرامیٹر کے تخمینے استعمال کرتے ہیں اور امید کرتے ہیں کہ ٹائم ونڈو کی لمبائی کو بہتر بنایا جائے۔ ہم تمام امکانات، مناسب وقت کی کھڑکی کی طوالت پر صرف اعادہ کرنے کا فیصلہ کر سکتے ہیں، اور اس وقت کا انتخاب کر سکتے ہیں جس کی بنیاد پر ہمارا ماڈل بہترین کارکردگی کا مظاہرہ کرے۔ ذیل میں ہم ٹریننگ ڈیٹا کے PNL کی بنیاد پر ٹائم ونڈو کی لمبائی کو اسکور کرنے کے لیے ایک سادہ لوپ لکھتے ہیں اور بہترین لوپ تلاش کرتے ہیں۔

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

اب ہم ٹیسٹ ڈیٹا پر ماڈل کی کارکردگی کو چیک کرتے ہیں، اور ہم دیکھتے ہیں کہ اس وقت ونڈو کی لمبائی زیادہ سے زیادہ نہیں ہے! اس کی وجہ یہ ہے کہ ہمارا اصل انتخاب واضح طور پر نمونے کے ڈیٹا سے زیادہ فٹ ہے۔

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

واضح طور پر جو ہمارے نمونے کے ڈیٹا کے لیے بہتر کام کرتا ہے وہ ہمیشہ مستقبل میں اچھے نتائج نہیں دیتا۔ صرف جانچ کے لیے، آئیے دو ڈیٹا سیٹس سے شمار کیے گئے طوالت کے اسکور کو پلاٹ کرتے ہیں۔

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

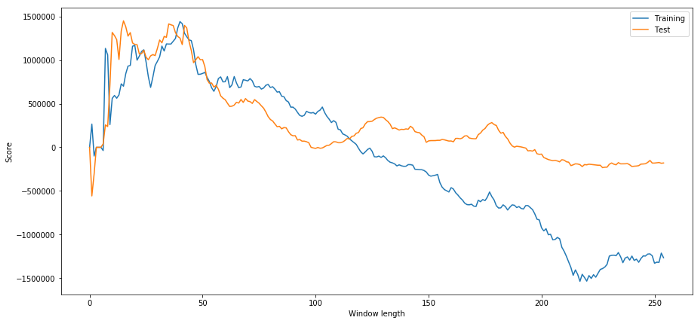
ہم دیکھ سکتے ہیں کہ 20-50 کے درمیان کوئی بھی چیز ٹائم ونڈو کے لیے ایک اچھا انتخاب ہے۔

اوور فٹنگ سے بچنے کے لیے، ہم اقتصادی استدلال یا الگورتھم کی خصوصیات کو استعمال کر کے ٹائم ونڈو کی لمبائی کا انتخاب کر سکتے ہیں۔ ہم کلمان فلٹر بھی استعمال کر سکتے ہیں، جس کے لیے ہمیں لمبائی بتانے کی ضرورت نہیں ہے۔

اگلا مرحلہ

اس مضمون میں، ہم تجارتی حکمت عملی تیار کرنے کے عمل کو ظاہر کرنے کے لیے کچھ آسان تعارفی طریقے پیش کرتے ہیں۔ عملی طور پر، زیادہ نفیس اعدادوشمار استعمال کیے جانے چاہئیں، اور آپ درج ذیل اختیارات پر غور کر سکتے ہیں:

• ہرسٹ ایکسپوننٹ

• Ornstein-Uhlenbeck کے عمل سے نکالے گئے اوسط الٹ جانے کی نصف زندگی

• کلمان فلٹر