Thông báo bản quyền: Nếu bạn muốn sao chép mã nguồn của bài viết này, xin hãy ghi rõ nguồn gốc, nếu sử dụng cho mục đích thương mại, hãy viết bài luận bằng thư cá nhân hoặc liên hệ với tác giả tại địa chỉ: 940648114@qq.com

1. Giới thiệu

Lợi thế của giao dịch định lượng

Giao dịch định lượng là sự phán đoán chủ quan của con người thay vì mô hình toán học tiên tiến, sử dụng công nghệ máy tính từ dữ liệu lịch sử khổng lồ để đưa ra chiến lược, giảm đáng kể ảnh hưởng của sự biến động tâm lý của nhà đầu tư, tránh đưa ra quyết định đầu tư phi lý trong trường hợp thị trường cực kỳ cuồng nhiệt hoặc bi quan.           Vì tiền kỹ thuật số 24*Sự liên tục của thị trường giao dịch 7 giờ liên tục, và giao dịch định lượng có thể đạt được hiệu quả của giao dịch tần số cao, bắt đầu từ thị trường tiền kỹ thuật số rõ ràng là một khởi đầu tốt để định lượng. Hiện tại thị trường tiền kỹ thuật số vẫn chưa trưởng thành.

Mô hình GQNR

Mô hình này dựa trên mô hình Garch dự đoán tỷ lệ dao động, và sử dụng sự hồi phục phi tuyến tính bằng cách quay trở số phân số VaR dự đoán tỷ lệ dao động, ví dụ như GA để kết hợp để dự đoán VaR trên cùng và VaR dưới cùng trong chu kỳ tiếp theo, mô hình phương pháp này được gọi tắt là GQNR.

1. Mô-đun Garch

Trong phần này, chúng tôi sẽ giới thiệu chi tiết các suy luận cốt lõi của chiến lược Garch, một phương pháp có tính phổ biến nhất định trong thị trường tài chính và có thể đạt được hiệu quả dự đoán nhất định trong tiền kỹ thuật số.

1.1 Garch định nghĩa

Bản chất của mô hình ARCH là sử dụng một dãy bình phương di chuyển q của chuỗi bình phương còn lại để phù hợp với giá trị hàm chênh lệch hiện tại. Vì mô hình trung bình di chuyển có tính cắt ngang q của hệ số tự liên quan, mô hình ARCH thực sự chỉ áp dụng cho các hệ số tự liên quan ngắn hạn của hàm chênh lệch. Tuy nhiên, trong thực tế, một số hàm chênh lệch khác biệt của chuỗi dư thừa có tính tự quan trọng lâu dài, khi sử dụng hàm chênh lệch khác biệt phù hợp với mô hình ARCH, sẽ tạo ra các bậc trung bình di chuyển rất cao, làm tăng độ khó trong ước tính tham số và cuối cùng ảnh hưởng đến độ chính xác phù hợp của mô hình ARCH.          Để sửa chữa một vấn đề, một mô hình khác biệt điều kiện từ hồi quy rộng được đề xuất, mô hình này được viết tắt là GARCH ((p,q). Mô hình GARCH trên thực tế được hình thành dựa trên ARCH, thêm tính tự hồi quy của hàm chênh lệch p, nó có thể phù hợp hiệu quả với hàm chênh lệch có trí nhớ dài. Mô hình ARCH là một ví dụ đặc biệt của mô hình GARCH, mô hình GARCH của p = 0 (p, q).

1.2 Quá trình ARCH

        định nghĩa là σn trong vòng giao dịch n-1 ước tính sự biến động của tài sản trong vòng giao dịch n, mu là lợi nhuận hàng ngày, sau đó có thể ước tính không thiên vị dựa trên lợi nhuận trong vòng giao dịch gần nhất m: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         Làm những thay đổi sau: 1 chuyển đổi μn-i thành tỷ lệ phần trăm; 2 chuyển đổi m-1 thành m; 3 giả định μ = 0 và những thay đổi này không ảnh hưởng nhiều đến kết quả, theo phương trình trên, tỷ lệ dao động có thể được đơn giản hóa thành: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         nghĩa là bình phương của tỷ lệ dao động của mỗi chu kỳ có trọng lượng bằng 1/m, vì ước tính tỷ lệ dao động hiện tại, dữ liệu gần hơn nên được gán trọng lượng cao hơn, thì phương trình trên có thể được thay đổi thành: \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi là hệ số của lãi suất bình phương của chu kỳ giao dịch i, lấy giá trị tích cực và giá trị nhỏ hơn của i càng lớn, tổng trọng số là 1. Tiếp tục mở rộng, giả sử có một tỷ lệ chênh lệch dài VL, và trọng số tương ứng là γ, theo phương thức trên có thể có được:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

         Soω = γVL,公式(15) có thể được viết là: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\(         Theo cách thức trên, chúng ta có thể có được ARCH phổ biến \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 Quy trình GARCH

Mô hình GARCH (p,q) là sự kết hợp của mô hình ARCH (p) và EWMA (q), có nghĩa là tỷ lệ dao động không chỉ liên quan đến thu nhập giai đoạn trước p, mà còn liên quan đến chính giai đoạn trước q, thể hiện như sau: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         Theo cách thức trên, chúng ta có thể có được GARCH phổ biến ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 mô-đun QR

        Phần này sẽ giải thích về sự trở lại số phân số cơ bản, mô tả tầm quan trọng của số phân số chiến lược

2.1 Định nghĩa QR

Định số phân số là một phương pháp mô hình để ước tính mối quan hệ tuyến tính giữa một tập hợp các biến số của biến số X và các số phân của biến số Y được giải thích. Mô hình hồi quy trước đây thực sự là sự mong đợi điều kiện của các biến được giải thích. Người ta cũng quan tâm đến mối quan hệ giữa số trung bình của biến giải thích và phân số của phân bố biến được giải thích. Nó được đưa ra lần đầu tiên bởi Koenker và Bassett vào năm 1978.

2.2 Từ OLS đến QR

Phương pháp hồi quy thông thường là phép nhân đôi nhỏ nhất, tức là số bình phương của sai số tối thiểu: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\(         và mục tiêu của số phân số là giảm thiểu các giá trị tuyệt đối của sai sót được tăng trọng dựa trên các công thức trên và: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 Hình ảnh QR

Bạn có thể thấy rằng tất cả các mẫu đều được phân chia thành các không gian khác nhau bởi đường hồi quy, và đường hồi quy này trở thành đường phân chia.

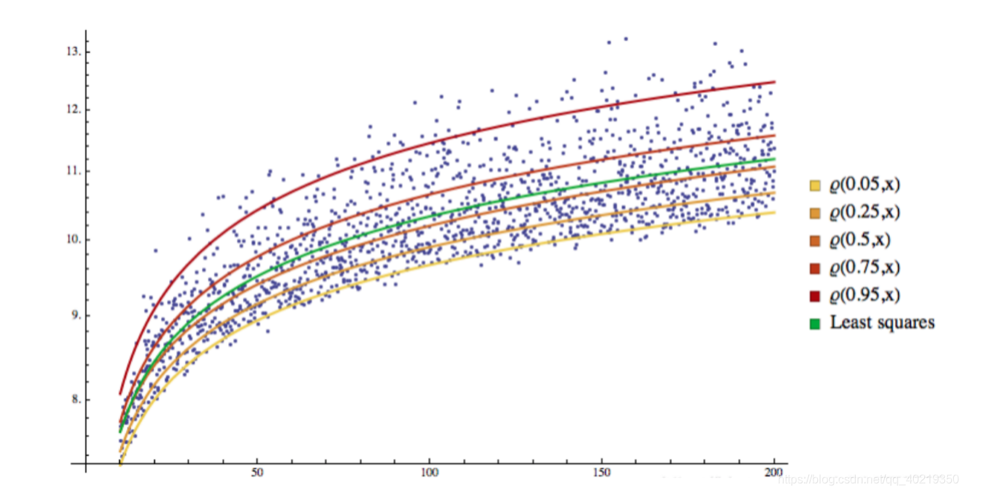
3. GARCH-QR regression

Chúng tôi tự nhiên nghĩ rằng liệu có thể sử dụng sigma của thị trường không biết biến động với phân số Q, VaR, để dự đoán suy giảm biến động trong tương lai trong trường hợp có khả năng, thị trường này sẽ đi theo hướng này.

3.1 Chọn biến động và hình thức trở lại của VaR

        Bởi vì đây là một phần cốt lõi của chiến lược, tôi tạm thời đưa ra một hình thức để giải thích suy nghĩ của mình. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Xác định hàm mục tiêu

        Dựa trên thông tin trên, chúng ta có thể kết hợp các hàm mục tiêu cuối cùng để tối ưu hóa: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Tối ưu hóa hàm mục tiêu bằng cách sử dụng học máy

Các bước này có nhiều tùy chọn hơn, độ dốc truyền thống giảm xuống, các thuật toán di truyền cũng có thể được sử dụng, người đọc có thể tự sáng tạo để thử nghiệm.có về địa chỉ thuật toán GA

Ba, cách sử dụng GQNR trong định lượng

1. Sự xác định của tư tưởng

Mặt khác, bằng cách dự đoán tỷ lệ biến động của dữ liệu trong quá khứ, có thể có được sự trở lại số phân số của giá trị biến động không vượt quá biên giới trên và biên giới dưới trong trường hợp có khả năng cao. Và hai biên giới này là cốt lõi của tổng thể. Khi kích hoạt biên giới trên, chúng ta có thể cho rằng có xu hướng điều chỉnh trong ngắn hạn dưới mức độ khả năng cao, và khi kích hoạt biên giới dưới, chúng ta có thể cho rằng có xu hướng tăng trong ngắn hạn dưới mức độ khả năng cao.

2. Những khó khăn trong việc sử dụng

• Dùng hình thức hồi quy
• Lựa chọn thuật toán thích ứng
• Các tham số thích hợp cho học máy
• Sự không chắc chắn và ngẫu nhiên của thị trường

3. Giải pháp

• Giảm thời gian học chiến lược
• Giảm bảo hiểm thế chấp đơn vị chống lại rủi ro dài hạn
• Tăng xác nhận xu hướng đường hai và xác nhận suy giảm thứ hai