উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং কৌশল সম্পর্কে চিন্তাভাবনা (3)
 0
0
 2664
2664

গত প্রবন্ধে, আমি কীভাবে ক্রমবর্ধমান ট্রেডিং ভলিউম মডেল করতে হয় তা উপস্থাপন করেছি এবং দামের প্রভাবের ঘটনাটি সংক্ষিপ্তভাবে বিশ্লেষণ করেছি। এই নিবন্ধটি ট্রেড অর্ডার ডেটা বিশ্লেষণ করতেও থাকবে। গত দুই দিনে, YGG Binance U-ভিত্তিক চুক্তি চালু করেছে, এবং ট্রেডিং ভলিউম এক সময়ে BTC ছাড়িয়ে গেছে।
অর্ডার সময় ব্যবধান
সাধারণ পরিস্থিতিতে, অনুমান করা হয় যে অর্ডারের আগমনের সময়টি পয়সন প্রক্রিয়ার সাথে সঙ্গতিপূর্ণবিষ প্রক্রিয়া . আমি নীচে এটি প্রমাণ করব।
5ই আগস্টে aggTrades ডাউনলোড করুন, মোট 1,931,193টি ট্রেড আছে, যা অত্যন্ত অতিরঞ্জিত। প্রথমত, ক্রয় অর্ডারের বন্টন দেখে নিন আপনি দেখতে পাচ্ছেন যে 100ms এবং 500ms এর কাছাকাছি রোবটটি নিয়মিত ব্যবধানে অর্ডার দেওয়ার কারণে এটি হতে পারে যে কারণে আজ বাজার অস্বাভাবিক ছিল।
পয়সন বন্টনের সম্ভাব্যতা ভর ফাংশন (PMF) দ্বারা দেওয়া হয়:
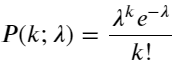
মধ্যে:
- k হল ইভেন্টের সংখ্যা যা আমরা আগ্রহী।
- λ হল প্রতি ইউনিট সময় (বা একক স্থান) ইভেন্টের গড় সংঘটন হার।
- P(k; λ) সম্ভাব্যতা উপস্থাপন করে যে ঠিক k ঘটনা ঘটবে গড় ঘটনার হার λ দেওয়া।
একটি পয়সন প্রক্রিয়ায়, ঘটনার মধ্যে সময়ের ব্যবধান একটি সূচকীয় বন্টন অনুসরণ করে। সূচকীয় বন্টনের সম্ভাব্যতা ঘনত্ব ফাংশন (PDF) দ্বারা দেওয়া হয়:
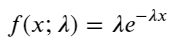
ফিটিং এর মাধ্যমে, এটি পাওয়া যায় যে ফলাফলগুলি পয়সন বিতরণের প্রত্যাশা থেকে সম্পূর্ণ ভিন্ন। (প্রকৃত ব্যবধানের বন্টন পরিবর্তিত প্যারেটো বিতরণের কাছাকাছি)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
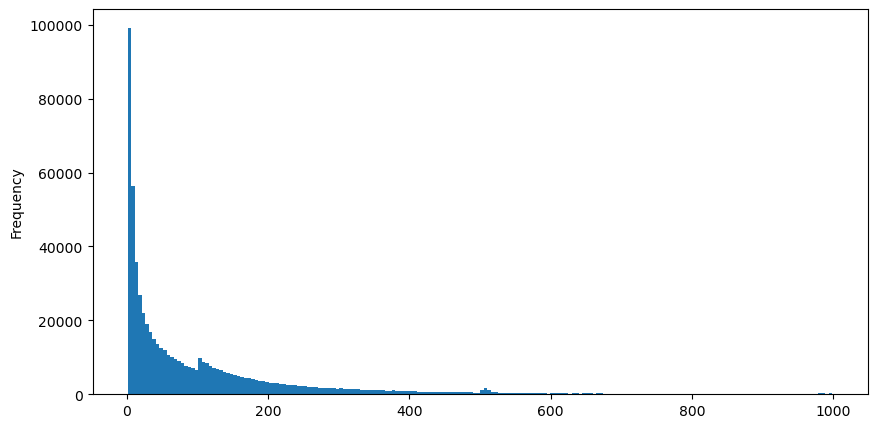
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
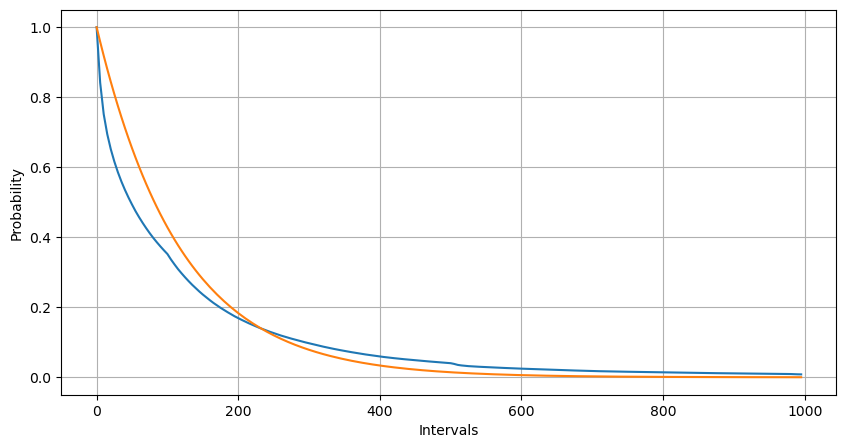
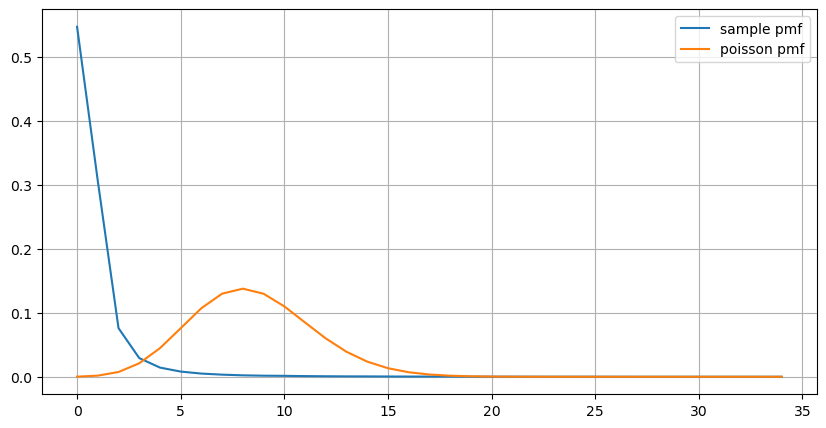
1 সেকেন্ডের মধ্যে সংঘটিত অর্ডারের ফ্রিকোয়েন্সি বিতরণের পরিসংখ্যানগুলি পয়সন বিতরণের সাথে তুলনা করা হয়। পয়সন ডিস্ট্রিবিউশন উল্লেখযোগ্যভাবে ছোট সম্ভাবনা ইভেন্টের ফ্রিকোয়েন্সি অবমূল্যায়ন করে। সম্ভাব্য কারণ:
- অ-কনস্ট্যান্ট সংঘটন হার: পয়সন প্রক্রিয়াটি ধরে নেয় যে কোনো নির্দিষ্ট সময়ের মধ্যে একটি ঘটনার গড় সংঘটনের হার ধ্রুবক। যদি এই অনুমান ধরে না থাকে, তবে ডেটা বিতরণ পয়সন বিতরণ থেকে বিচ্যুত হবে।
- প্রক্রিয়ার মিথস্ক্রিয়া: পয়সন প্রক্রিয়ার আরেকটি মৌলিক অনুমান হল ঘটনাগুলি স্বাধীন। যদি বাস্তব-বিশ্বের ঘটনা একে অপরের সাথে মিথস্ক্রিয়া করে, তবে তাদের বিতরণ পয়সন বিতরণ থেকে বিচ্যুত হতে পারে।
অর্থাৎ, একটি বাস্তব পরিবেশে, অর্ডারের ফ্রিকোয়েন্সি অ-স্থির এবং রিয়েল টাইমে আপডেট করা প্রয়োজন, এবং প্রণোদনা ঘটবে, অর্থাৎ, একটি নির্দিষ্ট সময়ের মধ্যে আরও অর্ডারগুলি আরও অর্ডারকে উদ্দীপিত করবে। এটি কৌশলটিকে একটি একক প্যারামিটার ঠিক করতে অক্ষম করে তোলে।
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
রিয়েল টাইমে পরামিতি আপডেট করুন
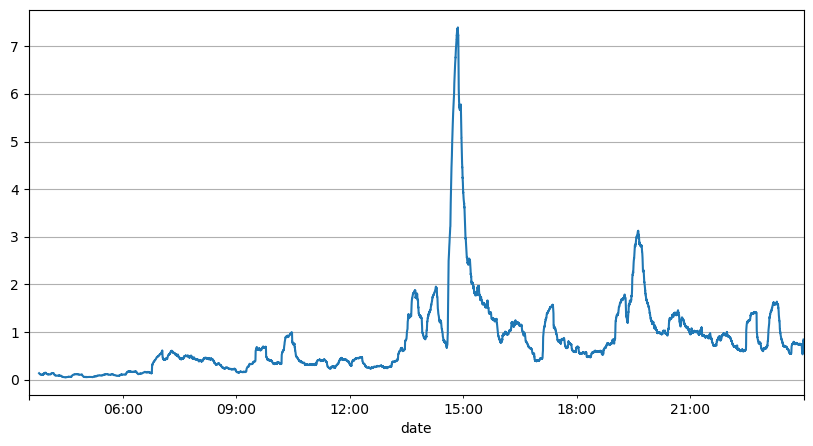
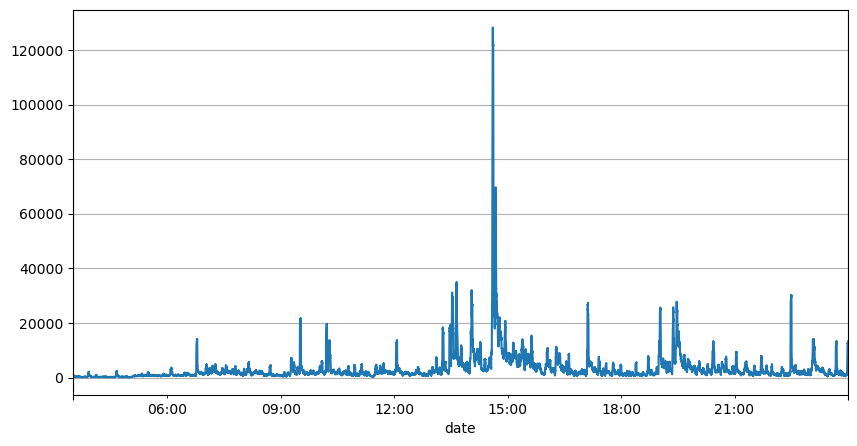
অর্ডার ব্যবধানের পূর্ববর্তী বিশ্লেষণ থেকে, এটি উপসংহারে পৌঁছানো যেতে পারে যে স্থির পরামিতিগুলি বাস্তব বাজারের অবস্থার জন্য উপযুক্ত নয় এবং কৌশলটির বাজারের বর্ণনার মূল পরামিতিগুলিকে বাস্তব সময়ে আপডেট করা দরকার। চিন্তা করার সবচেয়ে সহজ সমাধান হল একটি স্লাইডিং উইন্ডো মুভিং এভারেজ। নিম্নলিখিত দুটি ছবি হল 1 সেকেন্ডের মধ্যে কেনা অর্ডারের 1000-উইন্ডো ফ্রিকোয়েন্সি এবং লেনদেনের পরিমাণ দেখা যায় যে লেনদেনে একটি ক্লাস্টারিং ঘটনা রয়েছে, অর্থাৎ অর্ডারের ফ্রিকোয়েন্সি স্বাভাবিকের চেয়ে উল্লেখযোগ্যভাবে বেশি। একটি সময়কাল, এবং এই সময়ে ভলিউম একই সাথে বৃদ্ধি পায়। এখানে, পূর্ববর্তীটির গড় মানটি সর্বশেষ এক-সেকেন্ডের মানের ভবিষ্যদ্বাণী করতে ব্যবহৃত হয় এবং অবশিষ্টাংশের গড় পরম ত্রুটি ভবিষ্যদ্বাণীর গুণমান পরিমাপ করতে ব্যবহৃত হয়।
আমরা চিত্রটি থেকেও বুঝতে পারি যে কেন অর্ডার ফ্রিকোয়েন্সি পয়সন ডিস্ট্রিবিউশন থেকে এত বেশি বিচ্যুত হয় যদিও প্রতি সেকেন্ডে অর্ডারের গড় সংখ্যা মাত্র 8.5, চরম ক্ষেত্রে প্রতি সেকেন্ডে অর্ডারের গড় সংখ্যা অনেক দূরে।
এটি এখানে পাওয়া যায় যে পূর্ববর্তী দুই সেকেন্ডের গড় ব্যবহার করে অবশিষ্ট ত্রুটি ভবিষ্যদ্বাণী করা সবচেয়ে ছোট, এবং সাধারণ গড় ভবিষ্যদ্বাণী ফলাফলের চেয়ে অনেক ভালো।
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
সারসংক্ষেপ
এই নিবন্ধটি সংক্ষিপ্তভাবে কারণগুলি উপস্থাপন করে কেন অর্ডার সময়ের ব্যবধান পয়সন প্রক্রিয়া থেকে বিচ্যুত হয়, প্রধানত কারণ সময়ের সাথে পরামিতিগুলি পরিবর্তিত হয়। বাজারকে আরও সঠিকভাবে ভবিষ্যদ্বাণী করার জন্য, কৌশলগুলিকে বাজারের মৌলিক পরামিতিগুলির বাস্তব-সময়ের পূর্বাভাস দিতে হবে। ভবিষ্যদ্বাণীর গুণমান পরিমাপ করার জন্য অবশিষ্টাংশগুলি ব্যবহার করা যেতে পারে উপরেরটি সবচেয়ে সহজ উদাহরণ হল নির্দিষ্ট সময় সিরিজ বিশ্লেষণ, অস্থিরতা একত্রীকরণ ইত্যাদির উপর অনেকগুলি সম্পর্কিত অধ্যয়ন রয়েছে যা আরও উন্নত করা যেতে পারে৷