বেয়েজ - সম্ভাব্যতার রহস্যের সমাধান, সিদ্ধান্ত গ্রহণের পেছনের গাণিতিক জ্ঞান অনুসন্ধান

বেয়েজীয় পরিসংখ্যান হল গণিতের ক্ষেত্রে একটি শক্তিশালী শাখা, যার অর্থ, চিকিৎসা গবেষণা এবং তথ্য প্রযুক্তি সহ অনেক ক্ষেত্রে বিস্তৃত প্রয়োগ রয়েছে। এটি আমাদের পূর্ববর্তী বিশ্বাসগুলি প্রমাণের সাথে একত্রিত করতে নতুন পরবর্তী বিশ্বাসগুলি বের করতে সক্ষম করে, আমাদের আরও বুদ্ধিমান সিদ্ধান্ত নিতে সক্ষম করে।

এই নিবন্ধে, আমরা এই ক্ষেত্রের প্রতিষ্ঠাতা প্রধান গণিতবিদদের কিছু সংক্ষেপে পরিচয় করিয়ে দেব।

বেয়েসের আগে বেয়েজিয়ান পরিসংখ্যানকে আরও ভালভাবে বোঝার জন্য, আমাদের ১৮শ শতাব্দীতে ফিরে যেতে হবে এবং গণিতবিদ ডি মোইভ্রে এবং তার কাগজ The Doctrine of Chances উল্লেখ করতে হবে।

তার গবেষণাপত্রে, ডি মোভ্রে তার যুগে সম্ভাব্যতা এবং জুয়া সম্পর্কিত অনেক সমস্যার সমাধান করেছিলেন। যেমনটি আপনি জানেন, এই সমস্যাগুলির মধ্যে একটি সমাধানের ফলে স্বাভাবিক বন্টনের উৎপত্তি হয়েছিল, কিন্তু এটি অন্য গল্প।

তার গবেষণাপত্রের সবচেয়ে সহজ প্রশ্নগুলোর মধ্যে একটি ছিল:

একটি ন্যায্য মুদ্রা পরপর তিনবার নিক্ষেপ করলে তিনটি মাথা পাওয়ার সম্ভাবনা কত?

The Doctrine of Chances-এ বর্ণিত সমস্যাগুলি পড়লে আপনি লক্ষ্য করতে পারেন যে বেশিরভাগই একটি অনুমান দিয়ে শুরু করে যা থেকে তারা প্রদত্ত ইভেন্টগুলির জন্য সম্ভাব্যতা গণনা করে। উদাহরণস্বরূপ, উপরের প্রশ্নটিতে এমন একটি অনুমান রয়েছে যা মুদ্রাটিকে ন্যায্য বলে মনে করে; অতএব, নিক্ষেপের সময় মাথা পাওয়ার সম্ভাবনা 0.5।

এটাকে আজকে গণিতের ভাষায় প্রকাশ করা যেতে পারে:

সূত্র

𝑃(𝑋|𝜃)

কিন্তু যদি আমরা না জানি যে মুদ্রাটি ন্যায্য কিনা?𝜃 ?

টমাস বেজ এবং রিচার্ড প্রাইস

প্রায় পঞ্চাশ বছর পরে, 1763 সালে, রয়্যাল সোসাইটি অফ লন্ডনের দার্শনিক লেনদেনগুলিতে এ সলিউশন টু দ্য সমস্যা ইন দ্য ডক্টরিন অফ চ্যান্স শিরোনামে একটি কাগজ প্রকাশিত হয়েছিল।

এই নথির প্রথম কয়েক পৃষ্ঠায়, গণিতবিদ রিচার্ড প্রাইসের লেখা একটি টুকরো রয়েছে যা তার বন্ধু টমাস বেয়েসের মৃত্যুর কয়েক বছর আগে লেখা একটি কাগজকে সংক্ষিপ্ত করে। তার পরিচিতিতে, প্রাইস টমাস বেয়েসের কিছু গুরুত্বপূর্ণ আবিষ্কার ব্যাখ্যা করেছিলেন যা ডি মোভ্রে এর Doctrine of Chances এ উল্লেখ করা হয়নি।

প্রকৃতপক্ষে, তিনি একটি নির্দিষ্ট সমস্যার উল্লেখ করেছেন:

একটি অজানা ঘটনার সাফল্য ও ব্যর্থতার সংখ্যা দেওয়া হলে, দুটি নামযুক্ত ডিগ্রির মধ্যে এর সম্ভাবনা খুঁজে বের করুন।

অন্য কথায়, একটি ঘটনা পর্যবেক্ষণ করার পর আমরা নির্ধারণ করি যে একটি অজানা পরামিতির সম্ভাবনা কতθএটি আসলে ইতিহাসের পরিসংখ্যানগত অনুমানের সাথে সম্পর্কিত প্রথম সমস্যাগুলির মধ্যে একটি এবং এটি বিপরীত সম্ভাব্যতা শব্দটির জন্ম দিয়েছে। গাণিতিকভাবেঃ

সূত্র

𝑃( 𝜃 | 𝑋）

এটাকে আমরা আজকে বেয়েজ তত্ত্বের পিছনের বন্টন বলি।

কারণ ও ফলহীন কারণে

এই দুইজন প্রবীণ মন্ত্রীর গবেষণার পেছনের উদ্দেশ্য বুঝতে পেরে,টমাস বেজএবংরিচার্ড প্রাইসকিন্তু এটি করার জন্য, আমাদের অস্থায়ীভাবে পরিসংখ্যান সম্পর্কে কিছু জ্ঞান বাদ দিতে হবে।

আমরা ১৮ শতকে আছি যখন সম্ভাব্যতা গণিতবিদদের জন্য ক্রমবর্ধমান আকর্ষণীয় ক্ষেত্র হয়ে উঠছে। ডি মোভ্রে বা বার্নুলির মতো গণিতবিদরা ইতিমধ্যে দেখিয়েছেন যে কিছু ঘটনা একটি নির্দিষ্ট ডিগ্রি এলোমেলোতার সাথে ঘটে তবে এখনও স্থির নিয়ম দ্বারা পরিচালিত হয়। উদাহরণস্বরূপ, আপনি যদি একাধিকবার একটি পাশা নিক্ষেপ করেন তবে এক ষষ্ঠ অংশ সময় এটি ছয়টিতে অবতরণ করবে। এটি যেন একটি লুকানো নিয়ম রয়েছে যা ভাগ্য নির্ধারণের সম্ভাবনা নির্ধারণ করে।

এখন কল্পনা করুন যে আপনি একজন গণিতবিদ এবং এই সময়ে বসবাসকারী ধর্মপ্রাণ বিশ্বাসী। আপনি এই গোপন নিয়ম এবং ঈশ্বরের মধ্যে সম্পর্ক বুঝতে আগ্রহী হতে পারে।

এটি প্রকৃতপক্ষে বেয়েজ এবং প্রাইসের দ্বারা জিজ্ঞাসা করা প্রশ্ন ছিল। তারা আশা করেছিল যে তাদের সমাধান সরাসরি প্রমাণের জন্য প্রযোজ্য হবে বিশ্ব অবশ্যই জ্ঞান এবং বুদ্ধিমত্তার ফলাফল হতে হবে; অতএব চূড়ান্ত কারণ হিসাবে Godশ্বরের অস্তিত্বের প্রমাণ সরবরাহ করা - অর্থাৎ কারণহীন কারণ।

ল্যাপ্লেস

আশ্চর্যজনকভাবে, প্রায় দুই বছর পরে, ১৭৭৪ সালে, টমাস বেয়েজের কাগজটি না পড়ে ফরাসি গণিতবিদ ল্যাপ্লেস একটি কাগজ লিখেছিলেন যার শিরোনাম ছিল ঘটনার সম্ভাব্যতা দ্বারা ঘটনার কারণ সম্পর্কে , যা বিপরীত সম্ভাব্যতার সমস্যা সম্পর্কে। প্রথম পৃষ্ঠায়, আপনি মূল নীতিটি পড়তে পারেনঃ

যদি কোনো ঘটনা nটি ভিন্ন কারণে হতে পারে, তাহলে এই কারণগুলির মধ্যে অনুপাত ঘটনাটি দেওয়া সম্ভাব্যতা এই কারণগুলি দেওয়া ঘটনাগুলির সম্ভাব্যতার সমান; এবং প্রতিটি কারণের অস্তিত্বের সম্ভাব্যতা এই ঘটনাটি দেওয়া ঘটনার সম্ভাব্যতা দ্বারা ভাগ করা ঘটনার মোট সম্ভাব্যতার সমান।

এটিই আমরা আজকে বেয়েজ তত্ত্ব হিসাবে জানিঃ

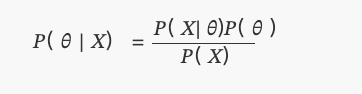
কোথায়P(θ)একটি অভিন্ন বন্টন।

মুদ্রা পরীক্ষা

আমরা পাইথন এবং PyMC লাইব্রেরি ব্যবহার করে বর্তমানের মধ্যে বেয়েজিয়ান পরিসংখ্যান আনব, এবং একটি সহজ পরীক্ষা পরিচালনা করব।

ধরুন আপনার বন্ধু আপনাকে একটি মুদ্রা দেয় এবং জিজ্ঞাসা করে যে আপনি কি মনে করেন যে এটি একটি ন্যায্য মুদ্রা। কারণ তার তাড়াহুড়ো আছে, সে আপনাকে বলে যে আপনি মুদ্রাটি কেবল 10 বার নিক্ষেপ করতে পারেন। আপনি দেখতে পারেন, একটি অজানা পরামিতি রয়েছেpএই সমস্যায়, যা মুদ্রা নিক্ষেপে মাথা পাওয়ার সম্ভাবনা, এবং আমরা সবচেয়ে সম্ভাব্য মান অনুমান করতে চাইp.

(দ্রষ্টব্যঃ আমরা যে পরামিতি বলছি নাpএকটি র্যান্ডম ভেরিয়েবল কিন্তু বরং যে এই পরামিতি স্থির হয়; আমরা জানতে চাই যেখানে এটি সবচেয়ে সম্ভবত মধ্যে)

এই সমস্যার উপর ভিন্ন ভিন্ন দৃষ্টিভঙ্গি থাকার জন্য, আমরা এটিকে দুটি ভিন্ন পূর্ববর্তী বিশ্বাসের অধীনে সমাধান করবঃ

• 1. আপনি মুদ্রার ন্যায্যতা সম্পর্কে কোন পূর্ববর্তী তথ্য আছে, তাই আপনি একটি সমান সম্ভাবনা নির্ধারণpএই ক্ষেত্রে, আমরা একটি non-informative prior ব্যবহার করব কারণ আপনি আপনার বিশ্বাসের কোন তথ্য যোগ করেননি।
• 2. আপনার অভিজ্ঞতা থেকে, আপনি জানেন যে এমনকি যদি একটি মুদ্রা অন্যায্য হতে পারে, এটা অত্যন্ত অন্যায্য করা কঠিন। অতএব, আপনি পরামিতি বিশ্বাসp0.3 এর চেয়ে কম বা 0.7 এর চেয়ে বেশি হওয়ার সম্ভাবনা কম। এই ক্ষেত্রে, আমরা একটি তথ্যমূলক পূর্ববর্তী ব্যবহার করব।

এই দুটি দৃশ্যের জন্য, আমাদের পূর্ববর্তী বিশ্বাসগুলি নিম্নরূপ হবেঃ

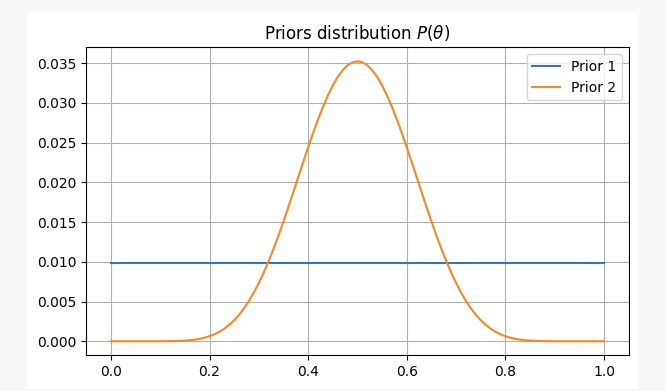
মুদ্রা ১০ বার ফেলার পর, আপনি দুইবার মাথা পেয়েছেন। এই প্রমাণের সাথে, আমরা কোথায় আমাদের পরামিতি খুঁজে পাবp?

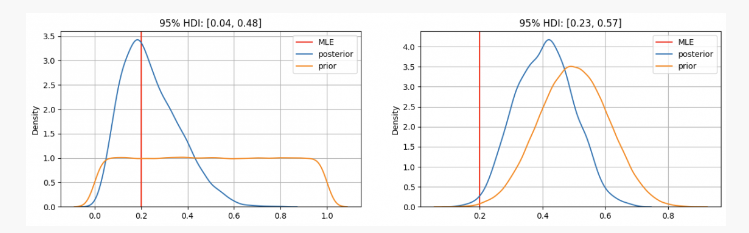
আপনি দেখতে পারেন, প্রথম ক্ষেত্রে, প্যারামিটার আমাদের পূর্ববর্তী বন্টনpসর্বাধিক সম্ভাব্যতা অনুমান (এমএলই) এ ঘনীভূত হয়p=0.2, যা ফ্রিকোয়েন্সি স্কুলে ব্যবহৃত পদ্ধতির অনুরূপ। সত্য অজানা পরামিতি 95% নির্ভরযোগ্যতার ব্যবধানের মধ্যে থাকবে, 0.04 এবং 0.48 এর মধ্যে।

অন্যদিকে, যেখানে উচ্চ নির্ভরযোগ্যতা আছে, সেই প্যারামিটারp0.3 এবং 0.7 এর মধ্যে হওয়া উচিত, আমরা দেখতে পাচ্ছি যে পিছনের বন্টনটি 0.4 এর কাছাকাছি, আমাদের এমএলই আমাদের যা দেয় তার চেয়ে অনেক বেশি। এই ক্ষেত্রে সত্য অজানা পরামিতি 0.23 এবং 0.57 এর মধ্যে 95% আত্মবিশ্বাসের ব্যবধানে থাকবে।

সুতরাং, প্রথম পরিস্থিতিতে আপনি আপনার বন্ধুকে নিশ্চিতভাবে বলবেন যে এই মুদ্রাটি ন্যায্য নয় কিন্তু অন্য পরিস্থিতিতে আপনি বলবেন যে এটি ন্যায্য কিনা তা অনিশ্চিত।

যেমন আপনি দেখতে পাচ্ছেন, এমনকি যখন একই প্রমাণের মুখোমুখি হন (দশটি নিক্ষেপের মধ্যে দুটি মাথা), বিভিন্ন পূর্ববর্তী বিশ্বাসের অধীনে ফলাফলগুলি ব্যাপকভাবে পরিবর্তিত হতে পারে; ঐতিহ্যগত পদ্ধতির তুলনায় বেয়েসিয়ান পরিসংখ্যানের একটি সুবিধা এখানে রয়েছেঃ বৈজ্ঞানিক পদ্ধতির মতো এটি আমাদের নতুন পর্যবেক্ষণ এবং প্রমাণের সাথে একত্রিত করে আমাদের বিশ্বাসগুলি আপডেট করতে দেয়।

END

আজকের প্রবন্ধে, আমরা বেয়েজিয়ান পরিসংখ্যানের উৎপত্তি এবং এর প্রধান অবদানকারীদের দেখেছি। পরবর্তীতে পরিসংখ্যানের এই ক্ষেত্রে অন্যান্য অনেক গুরুত্বপূর্ণ অবদানকারী (জেফ্রিস, কক্স, শ্যানন ইত্যাদি) রয়েছে, যা থেকে পুনরায় প্রকাশিত হয়েছেquantdare.com.