Python Naive Bayes-Anwendung

Unter der Voraussetzung, dass die Variablen unabhängig voneinander sind, kann die Klassifizierung nach dem Bayes-Theorem als naive Bayes-Klassifizierung betrachtet werden. Einfacher ausgedrückt: Ein naiver Bayes-Klassifizierer nimmt an, dass eine Eigenschaft der Klassifizierung unabhängig von den anderen Eigenschaften der Klassifizierung ist. Zum Beispiel, wenn eine Frucht rund und rot ist und etwa 3 Zoll im Durchmesser ist, kann diese Frucht eine Apfel sein.

• #### Ein einfaches Bayesianisches Modell ist einfach zu erstellen und sehr nützlich für große Datensätze. Obwohl es einfach ist, übersteigt es sehr komplexe Klassifizierungsmethoden.

Der Bayes-Theorem bietet eine Methode zur Berechnung der Nachprüfungswahrscheinlichkeit P © = x aus P © = c, P (x) = x und P (x) = c. Siehe folgende Gleichung:

Hier ist es so.

P © {\displaystyle \sigma © } ist die Wahrscheinlichkeit, dass die Klasse (Ziel) unter der Voraussetzung der bekannten Variablen (Attribute) der Vorhersage (Variablen) der Vorhersage (Ziel) der Klasse (Ziel) der Vorhersage (Ziel) der Vorhersage (Ziel) der Vorhersage (Ziel) der Vorhersage (Ziel) der Vorhersage (Ziel). P © ist die prioritäre Wahrscheinlichkeit der Klasse P (x) ist die Wahrscheinlichkeit, dass eine Variable unter der Annahme einer bekannten Klasse vorhergesagt wird. P (x) ist die vorherige Wahrscheinlichkeit der vorhergesagten Variablen Beispiel: Lassen Sie uns das Konzept anhand eines Beispiels verständlich machen. Im Folgenden habe ich eine Trainingsgruppe für Wetter und die entsprechende Zielvariable Play. Jetzt müssen wir die Spieler und Nicht-Spieler nach dem Wetter klassifizieren. Lassen Sie uns die folgenden Schritte ausführen:

Schritt 1: Umwandlung des Datensatzes in eine Frequenztabelle.

Schritt 2: Erstellen Sie ein Likelihood-Formular mit einer Wahrscheinlichkeit von 0,64, dass ein Spiel mit einer ähnlichen Spielchance gespielt wird, wenn die Overcast-Wahrscheinlichkeit 0,29 ist.

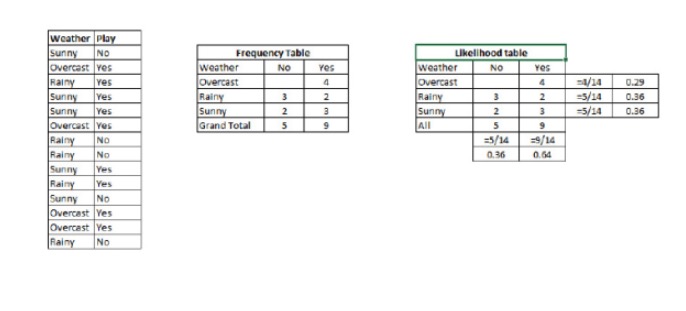
Schritt 3: Nun berechnen wir die Nachfolgewahrscheinlichkeit für jede Klasse anhand einer einfachen Bayesianischen Gleichung. Die Klasse mit der höchsten Nachfolgewahrscheinlichkeit ist die vorhergesagte Folge.

Frage: Ist diese Aussage richtig, wenn die Teilnehmer bei schönem Wetter spielen können?

Wir können das Problem mit den Methoden lösen, die wir diskutiert haben.

Wir haben P = ³⁄₉ = 0,33, P = ⁵⁄₁₄ = 0,36, P = ⁹⁄₁₄ = 0,64.

Nun, P {\displaystyle P} ist 0,33 * 0,64 / 0,36 = 0,60, und es gibt eine größere Wahrscheinlichkeit.

Ein ähnlicher Ansatz wurde von Nacho Bayes verwendet, um die Wahrscheinlichkeit verschiedener Kategorien durch verschiedene Attribute vorherzusagen. Dieser Algorithmus wird häufig für die Klassifizierung von Texten und für Probleme mit mehreren Kategorien verwendet.

• #### Python-Code:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)