Überlegungen zu Hochfrequenzhandelsstrategien (3)
 0
0
 2664
2664

Im vorherigen Artikel habe ich die Modellierung des kumulierten Handelsvolumens vorgestellt und das Preisschockphänomen kurz analysiert. In diesem Artikel werden weiterhin Handelsauftragsdaten analysiert. In den letzten zwei Tagen hat YGG Binance U-basierte Verträge aufgelegt, und der Preis schwankte stark, und das Handelsvolumen überstieg zeitweise sogar BTC. Lassen Sie es uns heute analysieren.
Bestellzeitintervall
Im Allgemeinen wird angenommen, dass die Zeit, in der Bestellungen eintreffen, einem Poisson-Prozess folgt. Hier ist ein Artikel, derPoisson-Prozess . Ich werde dies weiter unten demonstrieren.
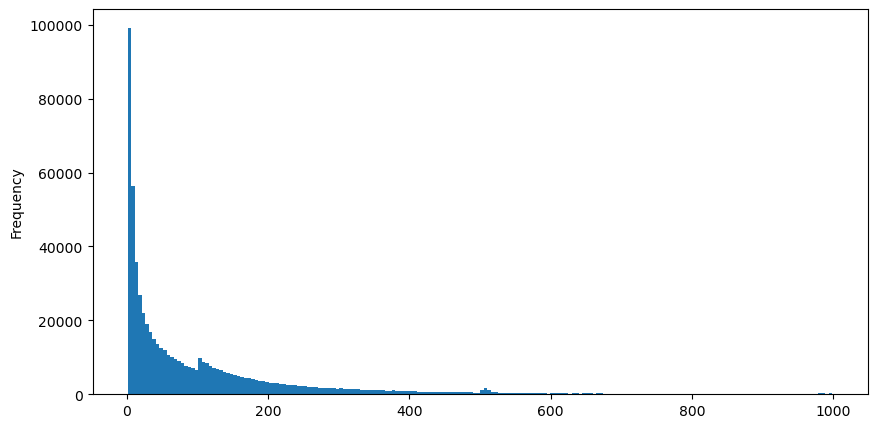
Laden Sie aggTrades am 5. August herunter, es gibt insgesamt 1.931.193 Trades, was ziemlich übertrieben ist. Schauen wir uns zunächst die Verteilung der Kaufaufträge an. Wir sehen, dass es bei etwa 100 ms und 500 ms einen ungleichmäßigen lokalen Peak gibt. Dies dürfte auf die geplanten Aufträge zurückzuführen sein, die der von Iceberg beauftragte Roboter erteilt hat. Dies könnte auch einer der der Gründe, warum die Marktbedingungen an diesem Tag ungewöhnlich waren.
Die Wahrscheinlichkeitsfunktion (PMF) der Poisson-Verteilung ergibt sich aus:
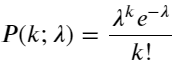
In:
- k ist die Anzahl der Ereignisse, die uns interessieren.
- λ ist die durchschnittliche Auftretensrate von Ereignissen pro Zeiteinheit (oder Raumeinheit).
- P(k; λ) ist die Wahrscheinlichkeit, dass bei einer durchschnittlichen Auftretensrate λ genau k Ereignisse eintreten.
In einem Poisson-Prozess folgen die Zeitintervalle zwischen Ereignissen einer Exponentialverteilung. Die Wahrscheinlichkeitsdichtefunktion (PDF) der Exponentialverteilung ergibt sich aus:
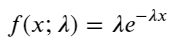
Durch Anpassung wurde festgestellt, dass die Ergebnisse stark von den erwarteten Ergebnissen der Poisson-Verteilung abwichen. Der Poisson-Prozess unterschätzte die Häufigkeit langer Intervalle und überschätzte die Häufigkeit kurzer Intervalle. (Die tatsächliche Intervallverteilung liegt näher an der modifizierten Pareto-Verteilung)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
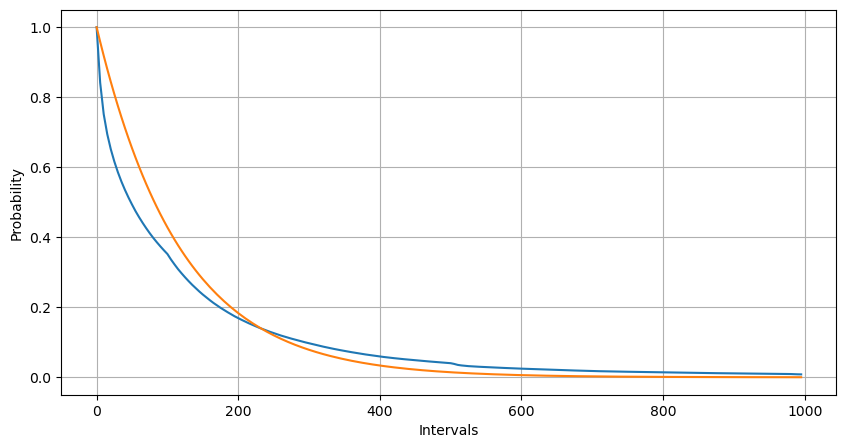
Auch die statistische Verteilung der Anzahl der innerhalb von 1 Sekunde auftretenden Ordnungen und der Vergleich mit der Poisson-Verteilung zeigen einen sehr deutlichen Unterschied. Die Poisson-Verteilung unterschätzt die Häufigkeit von Ereignissen mit geringer Wahrscheinlichkeit erheblich. Mögliche Ursachen:
- Nicht-konstante Auftretensrate: Der Poisson-Prozess geht davon aus, dass die durchschnittliche Häufigkeit von Ereignissen, die in einem bestimmten Zeitraum auftreten, konstant ist. Wenn diese Annahme nicht zutrifft, weicht die Verteilung der Daten von einer Poisson-Verteilung ab.
- Wechselwirkung der Prozesse: Eine weitere Grundannahme des Poisson-Prozesses ist, dass die Ereignisse voneinander unabhängig sind. Wenn reale Ereignisse sich gegenseitig beeinflussen, kann ihre Verteilung von der Poisson-Verteilung abweichen.
Das heißt, in einer realen Umgebung ist die Häufigkeit der Bestellungen nicht konstant und muss in Echtzeit aktualisiert werden. Außerdem treten Anreize auf, d. h. mehr Bestellungen in einer festgelegten Zeit stimulieren mehr Bestellungen. Dies macht es unmöglich, einen einzelnen Parameter in der Strategie festzulegen.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
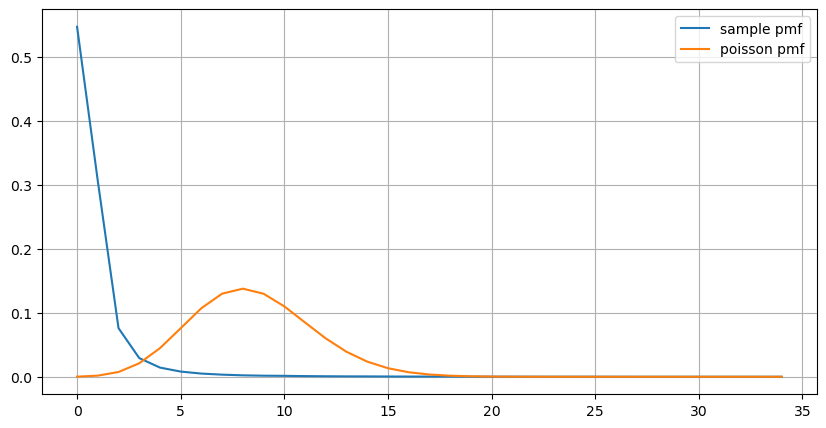
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Echtzeit-Update-Parameter
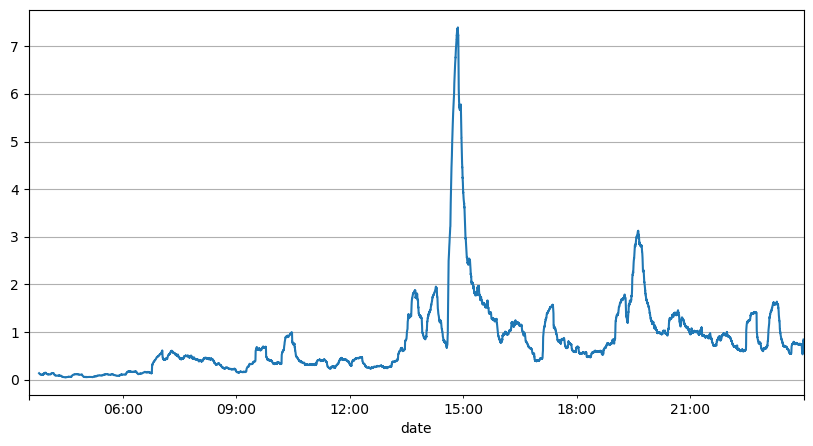
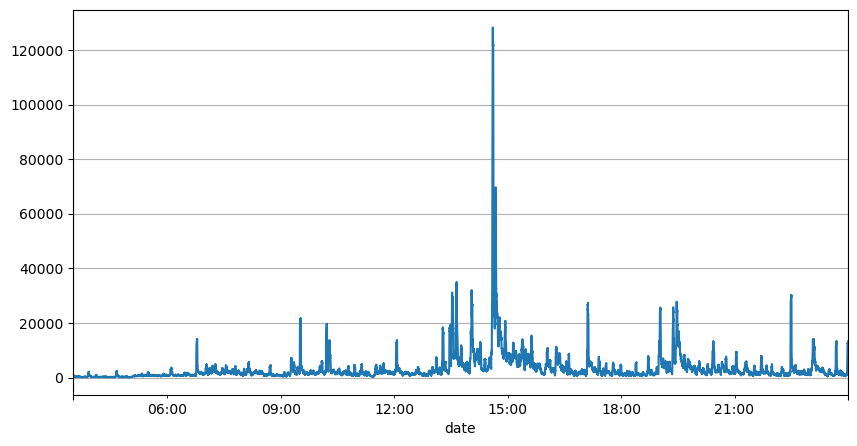
Die vorherige Analyse der Auftragsintervalle zeigt, dass feste Parameter für reale Marktbedingungen nicht geeignet sind und die Schlüsselparameter der Marktbeschreibung der Strategie in Echtzeit aktualisiert werden müssen. Die einfachste Lösung ist der gleitende Durchschnitt des gleitenden Fensters. Die beiden folgenden Zahlen zeigen die Häufigkeit von Kaufaufträgen innerhalb von 1 Sekunde und den Durchschnitt von 1000 Fenstern des Handelsvolumens. Es ist ersichtlich, dass es ein Clusterphänomen bei Transaktionen gibt, d. h. die Häufigkeit der Aufträge ist deutlich höher als üblich für ein Zeitraum, und die Lautstärke steigt zu diesem Zeitpunkt auch synchron an. Hier wird der vorherige Mittelwert verwendet, um den Wert der letzten Sekunde vorherzusagen, und der mittlere absolute Fehler des Residuums wird verwendet, um die Qualität der Vorhersage zu messen.
Aus der Grafik lässt sich auch nachvollziehen, warum die Bestellhäufigkeit so stark von der Poisson-Verteilung abweicht. Zwar beträgt die mittlere Bestellanzahl pro Sekunde nur das 8,5-fache, in Extremfällen weicht die mittlere Bestellanzahl pro Sekunde jedoch weit davon ab.
Dabei wurde festgestellt, dass der Restfehler am geringsten ist, wenn der Mittelwert der letzten zwei Sekunden zur Vorhersage verwendet wird, und dass dies viel besser ist als das Ergebnis einer einfachen Mittelwertvorhersage.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Zusammenfassen
In diesem Artikel werden kurz die Gründe vorgestellt, warum das Bestellzeitintervall vom Poisson-Prozess abweicht, hauptsächlich weil sich die Parameter im Laufe der Zeit ändern. Um den Markt genauer vorherzusagen, muss die Strategie Echtzeitvorhersagen zu den grundlegenden Parametern des Marktes treffen. Residuen können verwendet werden, um die Qualität von Vorhersagen zu messen. Das obige Beispiel ist das einfachste. Es gibt viele verwandte Studien zur Zeitreihenanalyse, Volatilitätsaggregation usw., die weiter verbessert werden können.