1. Kurze Einführung

Tiefe neuronale Netzwerke sind in den letzten Jahren immer beliebter geworden. Sie lösen in vielen Bereichen bislang unlösbare Probleme und stellen ihre Leistungsfähigkeit unter Beweis. Bei der Vorhersage von Zeitreihen ist RNN der häufig verwendete neuronale Netzwerkpreis, da RNN nicht nur aktuelle Dateneingaben, sondern auch historische Dateneingaben hat. Wenn wir über RNN-Preisvorhersagen sprechen, sprechen wir natürlich oft über eine Art RNN : LSTM. In diesem Artikel wird ein auf PyTorch basierendes Modell zur Vorhersage von Bitcoin-Preisen erstellt. Obwohl es im Internet viele relevante Informationen gibt, sind diese immer noch nicht gründlich genug, und es gibt relativ wenige Leute, die Pytorch verwenden. Es ist immer noch notwendig, einen Artikel zu schreiben. Das Endergebnis ist die Verwendung des Eröffnungskurses, des Schlusskurses, Höchster Preis, niedrigster Preis und Transaktionsvolumen des Bitcoin-Marktes. Um den nächsten Schlusskurs vorherzusagen. Meine persönlichen Kenntnisse über neuronale Netze sind durchschnittlich und ich freue mich über Ihre Kritik und Korrektur. Dieses Tutorial wird von FMZ erstellt, dem Erfinder der quantitativen Handelsplattform für digitale Währungen (www.fmz.com). Willkommen in der QQ-Gruppe: 863946592 zur Kommunikation.

2. Daten und Referenzen

Ein entsprechendes Beispiel für eine Preisvorhersage: https://yq.aliyun.com/articles/538484 Detaillierte Einführung in das RNN-Modell: https://zhuanlan.zhihu.com/p/27485750 Ein- und Ausgabe von RNN verstehen: https://www.zhihu.com/question/41949741/answer/318771336 Über Pytorch: Offizielle Dokumentation https://pytorch.org/docs Suchen Sie selbst nach weiteren Informationen. Darüber hinaus sind zum Verständnis dieses Artikels einige Vorkenntnisse erforderlich, z. B. zu Pandas/Crawlern/Datenverarbeitung usw., aber es macht nichts, wenn Sie diese nicht kennen.

3. Parameter des PyTorch-LSTM-Modells

Parameter von LSTM:

Als ich diese dicht gepackten Parameter zum ersten Mal im Dokument sah, war meine Reaktion: Als ich langsam las, verstand ich es schließlich.

input_size: Die Merkmalsgröße des Eingabevektors x. Wenn der Schlusskurs zur Vorhersage des Schlusskurses verwendet wird, dann ist input_size = 1; wenn der Schlusskurs durch Eröffnungshoch und Schlusstief vorhergesagt wird, dann ist input_size = 4 hidden_size: Versteckte Ebenengröße num_layers: Anzahl der RNN-Schichten batch_first: Wenn True, ist die erste Eingabedimension batch_size. Dieser Parameter ist ebenfalls sehr verwirrend und wird weiter unten ausführlich beschrieben.

Eingabedatenparameter:

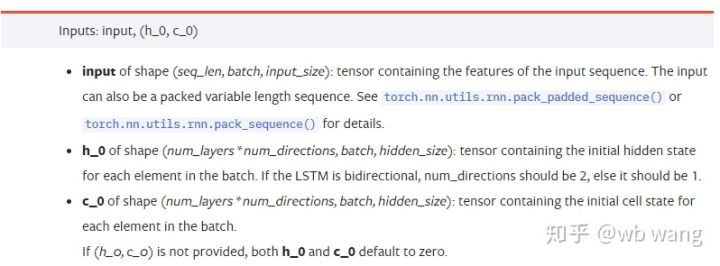
input: Die spezifischen Eingabedaten sind ein dreidimensionaler Tensor mit einer spezifischen Form von (Seq_Len, Batch, Input_Size). Unter ihnen bezieht sich seq_len auf die Länge der Sequenz, d. h., wie lange die historischen Daten LSTM berücksichtigen muss. Beachten Sie, dass sich dies nur auf das Format der Daten bezieht, nicht auf die interne Struktur des LSTM. Das gleiche LSTM-Modell kann Geben Sie Daten mit unterschiedlicher Sequenzlänge ein und können Sie Vorhersagen treffen. Ergebnis: Batch bezieht sich auf die Batchgröße, die angibt, wie viele unterschiedliche Datengruppen vorhanden sind; Eingabegröße ist die vorherige Eingabegröße. h_0: Anfänglicher verborgener Zustand, Form ist (Anzahl Ebenen * Anzahl Richtungen, Stapel, verborgene Größe), wenn es sich um ein bidirektionales Netzwerk handelt, ist Anzahl Richtungen = 2 c_0: Anfänglicher Zellzustand, die Form ist dieselbe wie oben, kann nicht angegeben werden.

Ausgabeparameter:

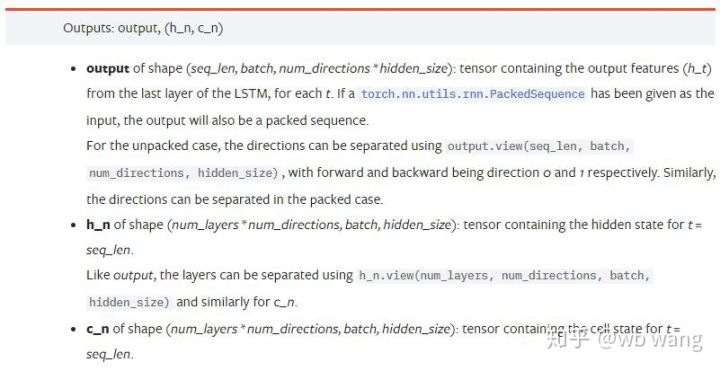
output: Ausgabeform (seq_len, batch, num_directions * hidden_size), beachten Sie, dass sie mit dem Modellparameter batch_first zusammenhängt h_n: h-Zustand zum Zeitpunkt t = seq_len, gleiche Form wie h_0 c_n: c-Zustand zum Zeitpunkt t = seq_len, gleiche Form wie c_0

4. Einfaches Beispiel für LSTM-Eingabe und -Ausgabe

Importieren Sie zunächst die benötigten Pakete

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Definieren des LSTM-Modells

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Vorbereiten der Eingabedaten

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

Die Form von x ist (3,4,5), da wir definiert habenbatch_first=True, zu diesem Zeitpunkt beträgt batch_size 3, sqe_len 4 und input_size 5. X[0] stellt die erste Charge dar.

Wenn batch_first nicht definiert ist, wird standardmäßig „False“ verwendet und die Daten werden völlig anders dargestellt, mit einer Batchgröße von 4, sqe_len von 3 und input_size von 5. Zu diesem Zeitpunkt x[0] stellt die Daten aller Chargen bei t=0 dar, und so weiter. Ich persönlich finde, dass diese Einstellung nicht intuitiv ist, deshalb habe ich den Parameter hinzugefügtbatch_first=True.

Auch die Konvertierung der Daten zwischen beiden ist sehr komfortabel:x.permute(1,0,2)

Ein- und Ausgabe

Die Form der LSTM-Ein- und -Ausgabe kann leicht verwechselt werden. Die folgende Abbildung soll dabei helfen, das Problem zu verstehen:
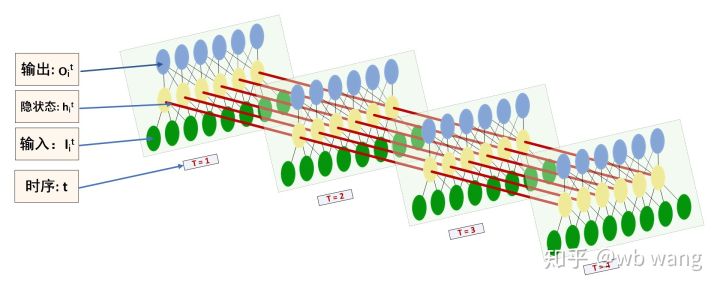
Quelle: https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Beachten Sie die Ausgabeergebnisse, die mit der vorherigen Parametererklärung übereinstimmen. Beachten Sie, dass der zweite Wert von hn.size() 3 ist, was mit der Größe von batch_size übereinstimmt und darauf hinweist, dass in hn kein Zwischenzustand gespeichert wird, sondern nur der letzte Schritt. Da unser LSTM-Netzwerk zwei Schichten hat, ist die Ausgabe der letzten Schicht von hn tatsächlich der Ausgabewert und die Form der Ausgabe ist[3, 4, 10] speichert die Ergebnisse aller Momente t=0,1,2,3, also:

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Bereiten Sie Bitcoin-Marktdaten vor

So viel von dem, was ich zuvor gesagt habe, ist nur ein Vorspiel. Es ist sehr wichtig, die Eingabe und Ausgabe von LSTM zu verstehen. Andernfalls können leicht Fehler gemacht werden, wenn Sie zufällig einige Codes aus dem Internet kopieren. Aufgrund der leistungsstarken Fähigkeit von LSTM in Zeitreihen, selbst wenn das Modell falsch ist, können Sie am Ende gute Ergebnisse erzielen.

Datenerfassung

Die verwendeten Daten sind die Marktdaten des BTC_USD-Handelspaares der Bitfinex-Börse.

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

Das Datenformat ist wie folgt:

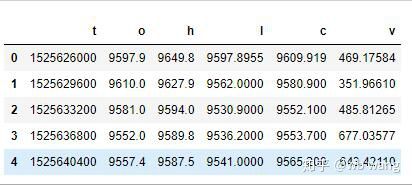
Datenvorverarbeitung

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

Die Methode der Datenstandardisierung ist sehr grob und es wird einige Probleme geben. Sie dient nur zur Demonstration. Sie können Datenstandardisierungen wie z. B. Yield verwenden.

Trainingsdaten vorbereiten

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

Die endgültigen Formen von train_x und train_y sind: torch.Size([800, 10, 5]), torch.Size([800, 10, 1]). Da unser Modell den Schlusskurs der nächsten Periode auf Grundlage der Daten aus 10 Perioden vorhersagt, sind für 800 Batches theoretisch nur 800 vorhergesagte Schlusskurse erforderlich. Aber train_y hat 10 Daten in jedem Batch. Tatsächlich werden die Zwischenergebnisse jeder Batch-Vorhersage beibehalten, nicht nur die letzte. Bei der Berechnung des endgültigen Verlusts können alle 10 Vorhersageergebnisse berücksichtigt und mit den tatsächlichen Werten in train_y verglichen werden. Theoretisch ist es auch möglich, nur den Verlust des letzten Prognoseergebnisses zu berechnen. Ich habe ein grobes Diagramm gezeichnet, um dieses Problem zu veranschaulichen. Da das LSTM-Modell den Parameter seq_len eigentlich nicht enthält, das Modell auf unterschiedliche Längen angewendet werden kann und die Zwischenvorhersageergebnisse auch aussagekräftig sind, neige ich dazu, die Berechnung des Verlusts zusammenzuführen.

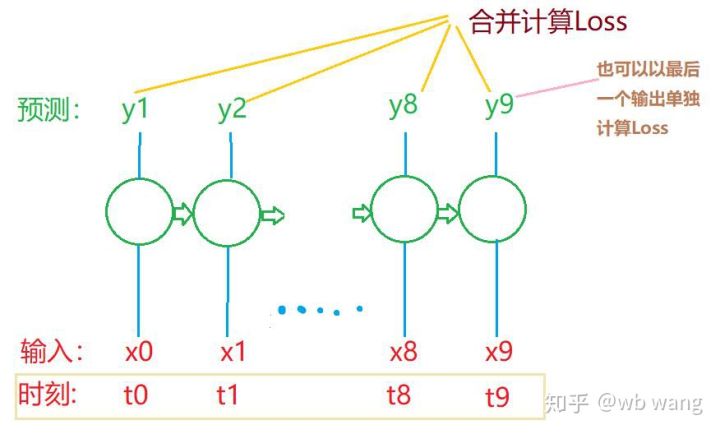
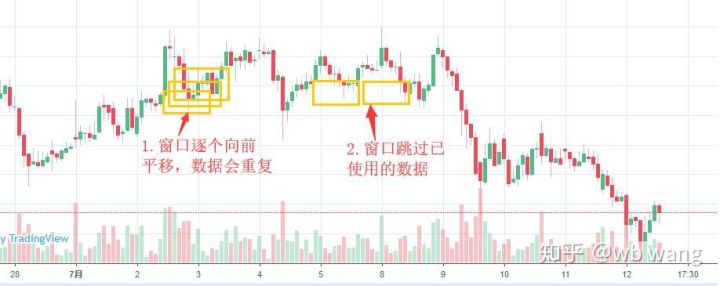
Beachten Sie, dass beim Vorbereiten der Trainingsdaten die Bewegung des Fensters sprunghaft ist und die verwendeten Daten nicht mehr verwendet werden. Natürlich können die Fenster auch einzeln verschoben werden, sodass der erhaltene Trainingssatz viel größer ist . Ich hatte jedoch das Gefühl, dass sich die angrenzenden Batchdaten zu sehr wiederholten, sodass ich die aktuelle Methode übernahm.

6. Erstellen eines LSTM-Modells

Das endgültige Modell sieht wie folgt aus und umfasst ein zweischichtiges LSTM und eine lineare Schicht.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. Beginnen Sie mit dem Training des Modells

Endlich ist das Training gestartet, der Code lautet wie folgt:

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
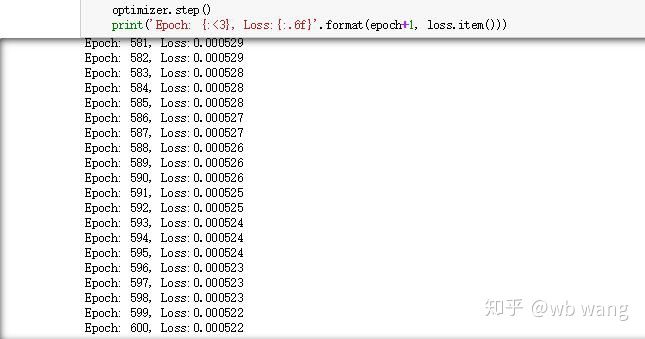
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Die Trainingsergebnisse sind wie folgt:

8. Modellbewertung

Die vom Modell vorhergesagten Werte sind:

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

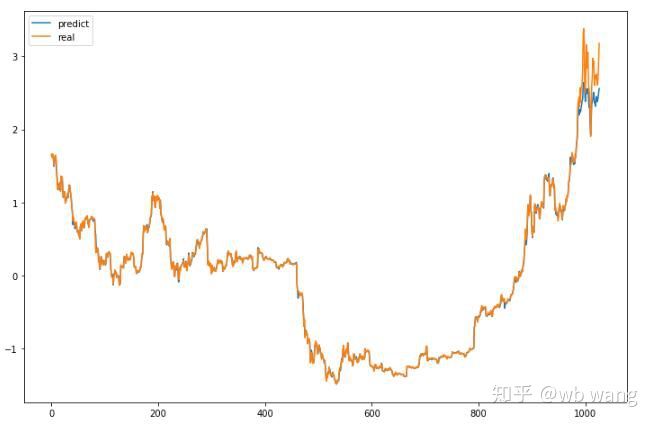
Wie aus der Abbildung ersichtlich ist, ist der Anpassungsgrad der Trainingsdaten (vor 800) sehr hoch, aber der Preis von Bitcoin ist später auf ein neues Hoch gestiegen, und das Modell hat diese Daten nicht gesehen, daher ist die Vorhersage nicht in der Lage, gute Leistungen zu erbringen. Dies zeigt auch, dass es bei der bisherigen Datenstandardisierung ein Problem gab. Auch wenn der vorhergesagte Preis möglicherweise nicht genau ist, wie genau ist die Vorhersage des Anstiegs und des Rückgangs? Sehen Sie sich einen Abschnitt der Vorhersagedaten an:

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

Die Genauigkeit der Vorhersage von Anstieg und Rückgang erreichte 81,4 % und übertraf damit meine Erwartungen. Ich weiß nicht, ob ich irgendwo einen Fehler gemacht habe.

Natürlich hat dieses Modell keinen wirklichen Wert, aber es ist einfach und leicht zu verstehen. Verwenden Sie es einfach als Ausgangspunkt. Es wird weitere Einführungskurse zur Anwendung neuronaler Netzwerke bei der Quantifizierung digitaler Währungen geben.