Reflexiones sobre estrategias de trading de alta frecuencia (3)
 0
0
 2664
2664

En el artículo anterior, presenté cómo modelar el volumen comercial acumulado y analicé brevemente el fenómeno del shock de precios. Este artículo continuará analizando los datos de órdenes comerciales. En los últimos dos días, YGG lanzó contratos basados en Binance U, y el precio fluctuó mucho, y el volumen de operaciones incluso superó a BTC en un momento dado. Analicémoslo hoy.
Intervalo de tiempo del pedido
En general, se supone que el tiempo en que llegan los pedidos sigue un proceso de Poisson. Aquí hay un artículo que presentaProceso de Poisson . Lo demostraré a continuación.
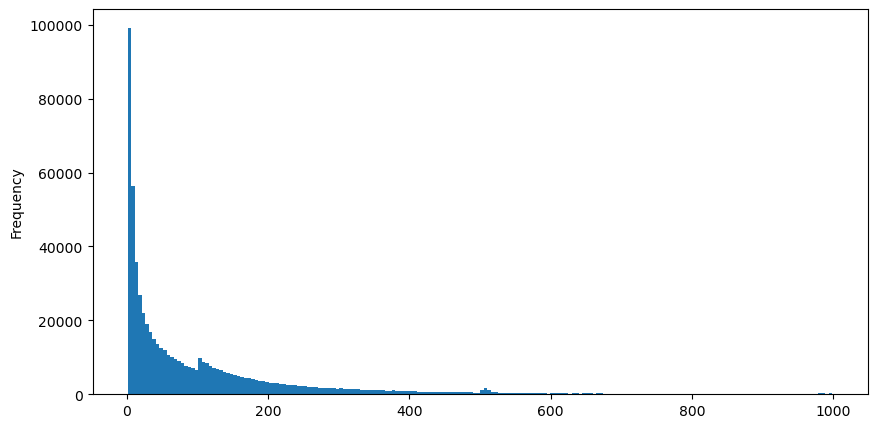
Descargue aggTrades el 5 de agosto, hay 1.931.193 operaciones en total, lo cual es bastante exagerado. En primer lugar, echemos un vistazo a la distribución de las órdenes de compra. Podemos ver que hay un pico local desigual en torno a los 100 ms y los 500 ms. Esto debería deberse a las órdenes programadas que coloca el robot encargado por Iceberg. Esta también puede ser una de las de las razones por las que las condiciones del mercado ese día eran inusuales.
La función de masa de probabilidad (PMF) de la distribución de Poisson viene dada por:
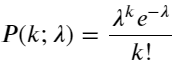
en:
- k es el número de eventos que nos interesan.
- λ es la tasa promedio de ocurrencia de eventos por unidad de tiempo (o unidad de espacio).
- P(k; λ) es la probabilidad de que ocurran exactamente k eventos, dada una tasa de ocurrencia promedio λ.
En un proceso de Poisson, los intervalos de tiempo entre eventos siguen una distribución exponencial. La función de densidad de probabilidad (PDF) de la distribución exponencial viene dada por:
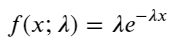
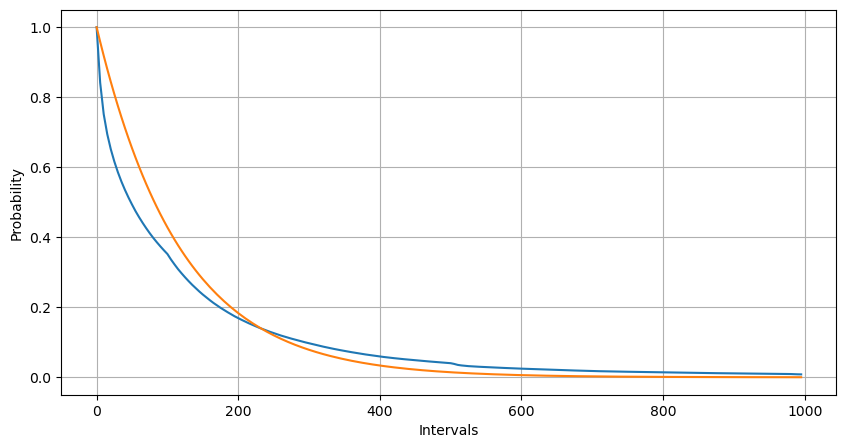
Mediante el ajuste, se encontró que los resultados eran bastante diferentes de los resultados esperados de la distribución de Poisson. El proceso de Poisson subestimó la frecuencia de intervalos largos y sobreestimó la frecuencia de intervalos cortos. (La distribución de intervalo real es más cercana a la distribución de Pareto modificada)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
La distribución estadística del número de órdenes que ocurren dentro de 1 segundo y la comparación con la distribución de Poisson también muestran una diferencia muy obvia. La distribución de Poisson subestima significativamente la frecuencia de eventos de baja probabilidad. Posibles causas:
- Tasa de ocurrencia no constante: el proceso de Poisson supone que la tasa promedio de eventos que ocurren en un período de tiempo determinado es constante. Si esta suposición no se cumple, entonces la distribución de los datos se desviará de una distribución de Poisson.
- Interacción de procesos: Otro supuesto básico del proceso de Poisson es que los eventos son independientes entre sí. Si los eventos del mundo real se influyen entre sí, su distribución puede desviarse de la distribución de Poisson.
Es decir, en un entorno real, la frecuencia de los pedidos no es constante, necesita actualizarse en tiempo real y se producirán incentivos, es decir, más pedidos en un tiempo fijo estimularán más pedidos. Esto hace imposible fijar un solo parámetro en la estrategia.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
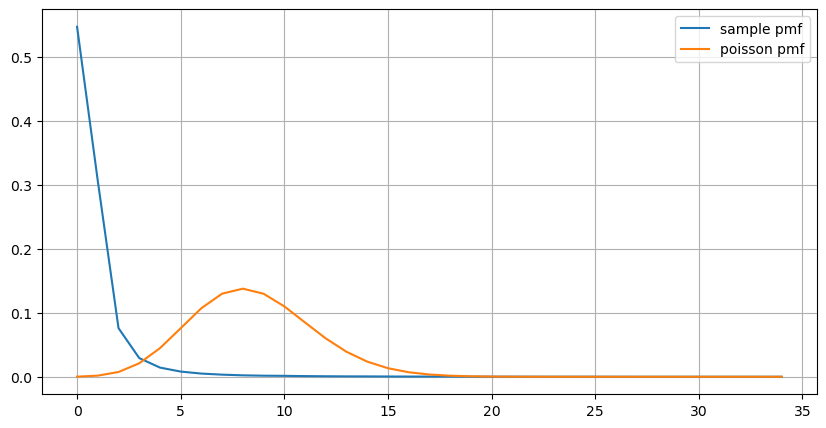
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Parámetros de actualización en tiempo real
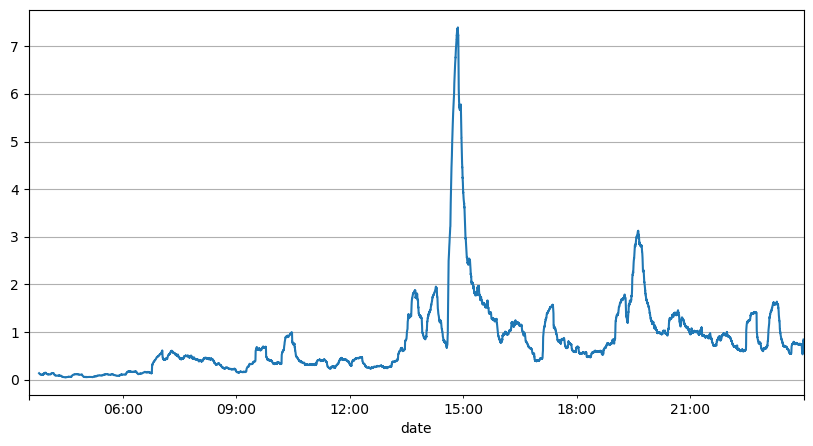
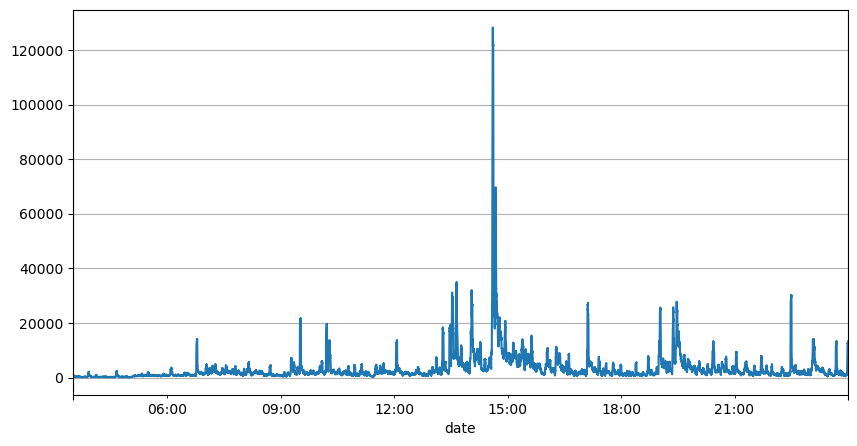
El análisis anterior de los intervalos de órdenes muestra que los parámetros fijos no son adecuados para las condiciones reales del mercado, y los parámetros clave de la descripción del mercado de la estrategia deben actualizarse en tiempo real. La solución más fácil de pensar es la media móvil de la ventana deslizante. Las dos cifras siguientes son la frecuencia de las órdenes de compra en un segundo y el promedio de 1000 ventanas de volumen de operaciones. Se puede observar que existe un fenómeno de agrupamiento en las transacciones, es decir, la frecuencia de las órdenes es significativamente mayor de lo habitual para una período de tiempo, y el volumen en este momento también aumenta sincrónicamente. Aquí, la media anterior se utiliza para predecir el valor del último segundo, y el error absoluto medio del residuo se utiliza para medir la calidad de la predicción.
A partir del gráfico, también podemos entender por qué la frecuencia de pedidos se desvía tanto de la distribución de Poisson. Aunque el número medio de pedidos por segundo es solo 8,5 veces, en casos extremos el número medio de pedidos por segundo se desvía mucho de ella.
Se descubre aquí que utilizar la media de los dos segundos anteriores para predecir el error residual es el más pequeño y es mucho mejor que el resultado de la predicción de la media simple.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Resumir
Este artículo presenta brevemente las razones por las que el intervalo de tiempo de orden se desvía del proceso de Poisson, principalmente porque los parámetros cambian con el tiempo. Para predecir el mercado con mayor precisión, la estrategia debe realizar predicciones en tiempo real sobre los parámetros básicos del mercado. Los residuos se pueden utilizar para medir la calidad de las predicciones. El ejemplo anterior es el más sencillo. Existen muchos estudios relacionados sobre análisis de series temporales, agregación de volatilidad, etc., que se pueden mejorar aún más.