Application Python Naive Bayes

Si les variables sont indépendantes les unes des autres, on obtient une classification simple selon le théorème de Bayes. En d’autres termes, un classificateur simple de Bayes suppose qu’une caractéristique d’une classification est sans rapport avec les autres caractéristiques de cette classification. Par exemple, si un fruit est rond et rouge et a un diamètre d’environ 3 pouces, alors il peut être une pomme.

• #### Les modèles Bayes simples sont faciles à construire et très utiles pour les grands ensembles de données. Bien qu’ils soient simples, les performances de Bayes simples dépassent les méthodes de classification très complexes.

Le théorème de Bayes fournit une méthode pour calculer la probabilité de retracement P (c < x) à partir de P ©, P (x) et P (x < c). Consultez l’équation suivante:

Je ne sais pas quoi dire.

P © {\displaystyle \sigma © } est la probabilité d’exécution de la classe (objectif) avec une variable de prédiction (attribut) connue. P © est la probabilité prioritaire de la classe P (x) {\displaystyle P (x) } est la probabilité, c’est-à-dire la probabilité de prédire une variable en supposant une classe connue. P (x) est la probabilité prioritaire de la variable de prédiction Exemple: pour comprendre ce concept, prenons un exemple. Ci-dessous, j’ai un ensemble d’entraînement pour la météo et la variable cible correspondante, le jeu. Maintenant, nous devons classer les joueurs et les non-joueurs en fonction de la météo.

Étape 1: Convertissez le jeu de données en tableaux de fréquences.

Étape 2: Créer un tableau de probabilité en utilisant une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,29 pour jouer avec une probabilité de 0,29 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,29 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,29 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,29 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer avec une probabilité de 0,64 pour jouer.

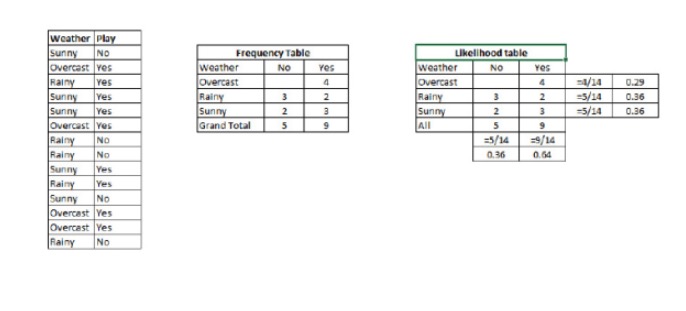
Étape 3: Maintenant, on calcule la post-probabilité de chaque classe en utilisant une simple équation de Bayes. La classe avec la plus grande post-probabilité est le résultat prévu.

Question: Est-ce que cette affirmation est correcte ?

Nous pouvons résoudre ce problème en utilisant la méthode que nous avons discutée. Donc P (jouer) = P (jouer) * P (jouer) / P (jouer).

Nous avons P = ³⁄₉ = 0,33, P = ⁵⁄₁₄ = 0,36, P = ⁹⁄₁₄ = 0,64.

Maintenant, P (jouer) est égal à 0,33 fois 0,64 / 0,36 = 0,60, il y a une plus grande probabilité que ce soit le cas.

La simplicité de Bayes utilise une méthode similaire pour prédire la probabilité de différentes catégories par différents attributs. Cette algorithme est généralement utilisé pour la classification de texte, ainsi que pour des problèmes impliquant plusieurs catégories.

• #### Le code Python:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)