Aplikasi Naive Bayes Python

Dengan asumsi bahwa variabel-variabel tersebut saling independen, maka dapat diperoleh metode klasifikasi Bayes yang sederhana berdasarkan teorema Bayes. Dengan kata lain, sebuah klasifikasi Bayes yang sederhana mengasumsikan bahwa satu sifat dari suatu klasifikasi tidak berhubungan dengan sifat-sifat lainnya dari klasifikasi tersebut. Sebagai contoh, jika sebuah buah bulat dan merah, dan berdiameter sekitar 3 inci, maka buah tersebut mungkin merupakan sebuah apel. Bahkan jika sifat-sifat tersebut saling bergantung satu sama lain, atau bergantung pada sifat-sifat lain, klasifikasi Bayes yang sederhana akan mengasumsikan bahwa sifat-sifat tersebut secara independen mengisyaratkan bahwa buah tersebut adalah sebuah apel.

• #### Model Bayesian sederhana mudah dibangun, dan sangat berguna untuk dataset besar. Meskipun sederhana, Bayesian sederhana berkinerja melampaui metode klasifikasi yang sangat rumit.

Teorema Bayes memberikan sebuah metode untuk menghitung probabilitas retrospektif P (c atau x) dari P ©, P (x) dan P (x). Lihat persamaan berikut:

Di sini,

P (c < c < x) adalah probabilitas terbalik dari kelas (< target) dengan asumsi bahwa variabel prediksi (< sifat) diketahui P © adalah probabilitas awal dari kelas P (x) adalah probabilitas, yaitu probabilitas prediksi variabel dengan asumsi kelas yang diketahui. P (x) adalah probabilitas awal dari variabel prediksi Contoh: Mari kita pahami konsep ini dengan sebuah contoh. Di bawah ini, saya memiliki set latihan cuaca dan variabel target yang sesuai dengan Play . Sekarang, kita perlu mengklasifikasikan peserta yang akan bermain dan yang tidak bermain berdasarkan kondisi cuaca. Mari kita lakukan langkah-langkah berikut.

Langkah 1: Konversi dataset ke tabel frekuensi.

Langkah 2: Buat tabel Likelihood dengan probabilitas seperti 0.64 jika probabilitas Overcast adalah 0.29 dan probabilitas bermain adalah 0.64 jika probabilitas Overcast adalah 0.29 dan probabilitas bermain adalah 0.64.

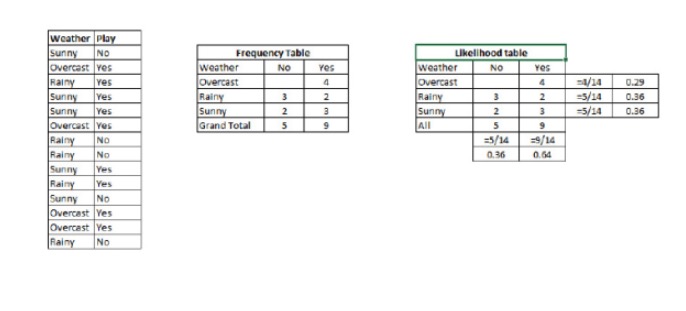
Langkah 3: Sekarang, gunakan persamaan Bayes sederhana untuk menghitung probabilitas terbalik dari setiap kelas. Kelas dengan probabilitas terbalik terbesar adalah hasil yang diprediksi.

Pertanyaan: Apakah pernyataan ini benar bahwa peserta dapat bermain jika cuaca cerah?

Kita bisa menggunakan metode yang telah kita bahas. Jadi P (bermain) = P (bermain) / P (bermain).

Jadi kita punya P = ³⁄₉ = 0.33, P = ⁵⁄₁₄ = 0.36, P = ⁹⁄₁₄ = 0.64.

Sekarang, P (bermain) = 0.33 * 0.64 / 0.36 = 0.60, ada kemungkinan yang lebih besar.

Bayes yang polos menggunakan metode serupa untuk memprediksi probabilitas dari berbagai kategori dengan berbagai atribut. Algoritma ini biasanya digunakan untuk mengklasifikasikan teks, dan untuk masalah yang melibatkan beberapa kategori.

• #### Kode Python:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)