高頻度取引戦略についての考察(3)
 0
0
 2665
2665

前回の記事では、累計取引量をモデル化する方法を紹介し、価格ショック現象について簡単に分析しました。この記事では、引き続き取引注文データを分析します。過去2日間、YGGはBinance Uベースの契約を開始し、価格が大きく変動し、取引量は一時BTCを超えました。今日はそれを分析してみましょう。
注文時間間隔
一般的に、注文が到着する時間はポアソン過程に従うと想定されています。ここでは、ポアソン過程 。以下でこれを説明します。
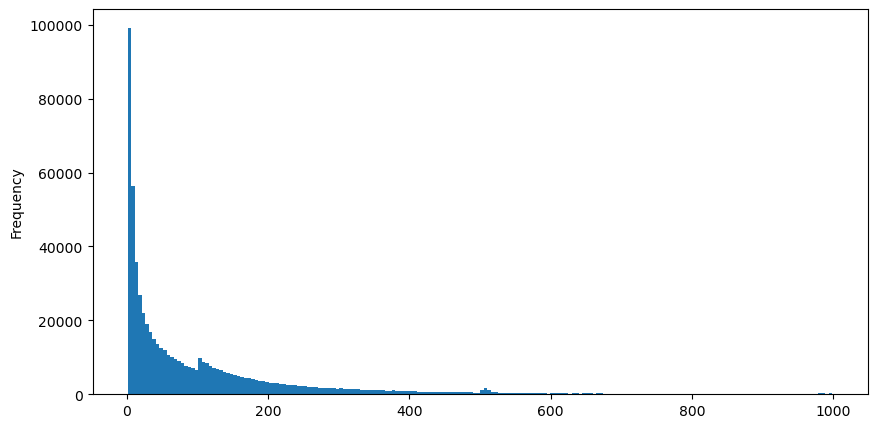
8月5日にaggTradesをダウンロードすると、合計1,931,193件の取引があり、かなり誇張されています。まず、買い注文の分布を見てみましょう。100msと500ms付近に不均一な局所的なピークがあることがわかります。これは、アイスバーグに委託されたロボットが発注したスケジュールされた注文が原因であると考えられます。これも、その日の市場状況が異常であった理由について。
ポアソン分布の確率質量関数 (PMF) は次のように表されます。
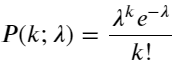
で:
- k は、関心のあるイベントの数です。
- λ は単位時間(または単位空間)あたりのイベントの平均発生率です。
- P(k; λ)は、平均発生率λが与えられた場合に、ちょうどk個のイベントが発生する確率です。
ポアソン過程においては、イベント間の時間間隔は指数分布に従います。指数分布の確率密度関数 (PDF) は次のように表されます。
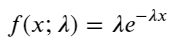
フィッティングにより、結果はポアソン分布の予想結果とはかなり異なることがわかりました。ポアソン過程は長い間隔の頻度を過小評価し、短い間隔の頻度を過大評価しました。 (実際の区間分布は修正パレート分布に近いです)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
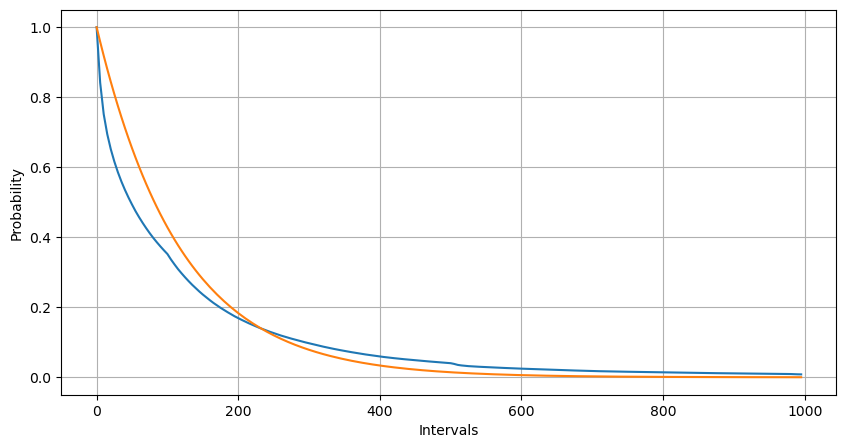
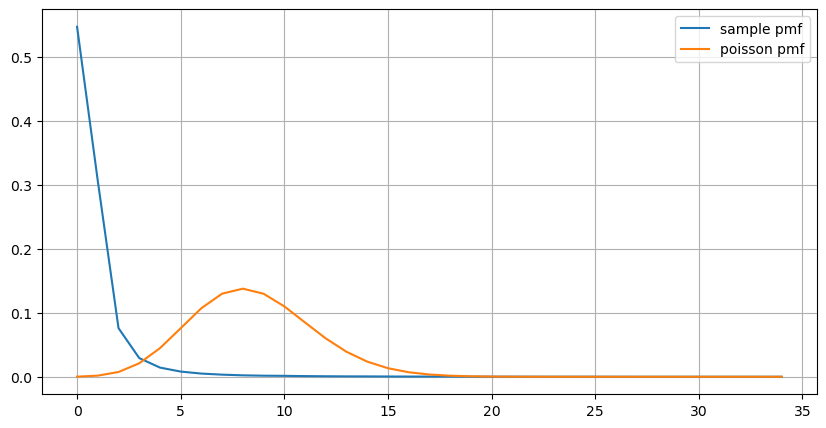
1 秒以内に発生する注文数の統計分布とポアソン分布との比較でも、非常に明らかな違いが見られます。ポアソン分布は、低確率のイベントの頻度を大幅に過小評価します。考えられる原因:
- 発生率が一定でない: ポアソン過程は、特定の期間に発生するイベントの平均発生率が一定であると想定します。この仮定が成り立たない場合、データの分布はポアソン分布から外れます。
- プロセスの相互作用: ポアソン過程のもう 1 つの基本的な仮定は、イベントが互いに独立しているということです。現実世界の出来事が相互に影響し合う場合、その分布はポアソン分布から逸脱する可能性があります。
つまり、実際の環境では、注文の頻度は一定ではなく、リアルタイムで更新する必要があり、インセンティブが発生します。つまり、一定時間内に注文が増えると、より多くの注文が刺激されます。これにより、戦略内の単一のパラメータを固定することは不可能になります。
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
リアルタイム更新パラメータ
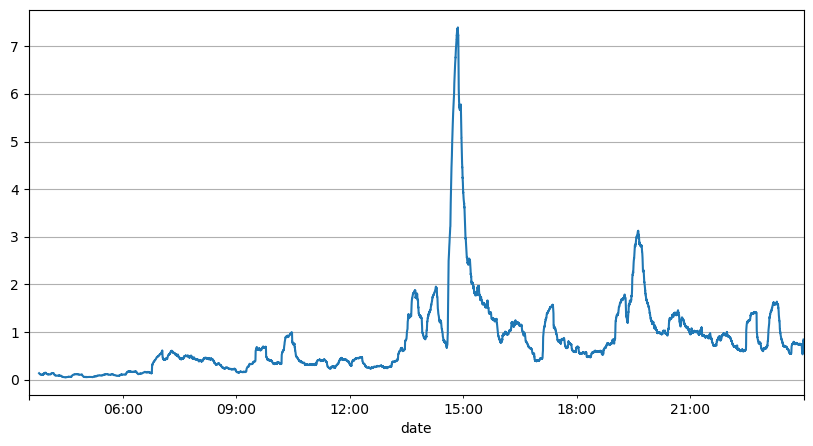
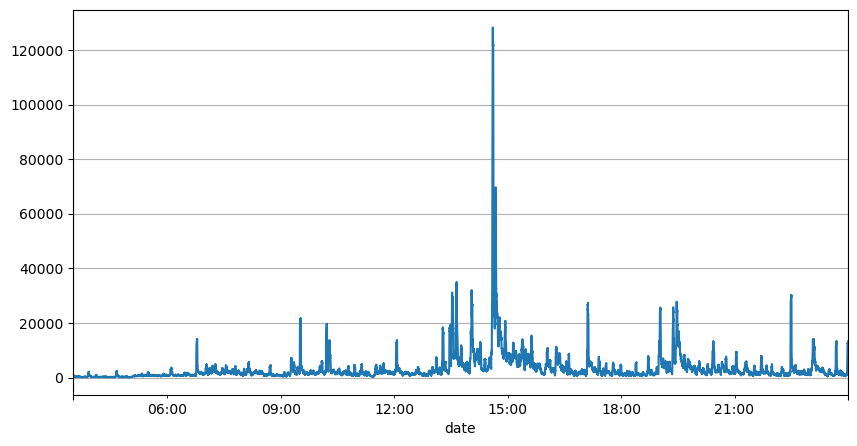
注文間隔のこれまでの分析では、固定パラメータは実際の市場状況には適しておらず、戦略の市場説明の主要パラメータはリアルタイムで更新する必要があることが示されています。考えられる最も簡単な解決策は、スライディング ウィンドウの移動平均です。下の2つの図は、1秒以内の買い注文の頻度と、取引量1000ウィンドウの平均です。取引にクラスタリング現象が発生していることがわかります。つまり、注文の頻度が通常よりも大幅に高くなっています。一定期間が経過し、このときの音量も同期して増加します。ここでは、前回の平均を使用して最新の秒の値を予測し、残差の平均絶対誤差を使用して予測の品質を測定します。
グラフから、注文頻度がポアソン分布から大きく外れている理由もわかります。1 秒あたりの平均注文数はわずか 8.5 回ですが、極端な場合には 1 秒あたりの平均注文数はそこから大きく外れます。
ここでは、過去 2 秒間の平均を使用して残差誤差を予測すると、最小になり、単純な平均予測結果よりもはるかに優れていることがわかります。
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
要約する
この記事では、主にパラメータが時間の経過とともに変化するために、注文時間間隔がポアソン過程から逸脱する理由を簡単に紹介します。市場をより正確に予測するためには、戦略によって市場の基本的なパラメータをリアルタイムで予測する必要があります。残差は予測の質を測定するために使用できます。上記の例は最も単純なものです。時系列分析、ボラティリティ集約など、さらに改善できる関連研究は数多くあります。