파이썬 나이브 베이즈 응용 프로그램

예측 변수들 사이의 상호 독립성을 전제로, 베이즈 이론에 따라 순수 베이즈의 분류법을 얻을 수 있다. 더 간단하게 말해서, 순수 베이즈 분류자는 분류의 한 특성이 그 분류의 다른 특성과 관련이 없다는 것을 가정한다. 예를 들어, 만약 과일도 둥글고 빨간색이고 지름이 약 3인치인다면, 그 열매는 사과일 수 있다. 이러한 특성이 서로 의존하거나 다른 특성에 의존하더라도, 순수 베이즈 분류자는 이러한 특성이 개별적으로 존재한다고 가정하여 과일이 사과라는 것을 암시한다.

• #### 단순 베이스 모델은 쉽게 만들 수 있으며, 큰 데이터 세트에서 매우 유용하다. 단순하지만 단순 베이스 모델은 매우 복잡한 분류 방법을 뛰어넘는다.

베이스 정리 (Beyes theorem) 는 P © 와 P (x) 와 P (x) 와 P © 에서 P © 와 C (x) 의 후진 확률을 계산하는 방법을 제공한다. 다음 방정식을 참조하십시오:

여기,

P © 는 예측 변수 (属性) 가 알려진 경우, 클래스 (목적) 의 후시험 확률이다. P © 는 클래스의 선행 확률이다. P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn Yksi) on todennäköisyys, joka ennustaa muuttujan, jos muuttujan luonne on tiedossa. P (x) 는 예측 변수의 선행 확률이다. 예: 이 개념을 한 가지 예로 설명해 보겠습니다. 아래에는 날씨에 대한 훈련 세트와 그에 따른 목표 변수인 Play이 있습니다. 이제 우리는 날씨에 따라 플레이하는 사람과 그렇지 않은 참가자를 분류해야 합니다. 다음 단계를 수행해 보겠습니다.

1단계: 데이터 세트를 주파수 표로 변환합니다.

2단계: 오버캐스트 확률이 0.29일 때, 놀이의 확률이 0.64일 때, 비슷한 을 사용하여 Likelihood 표를 생성한다.

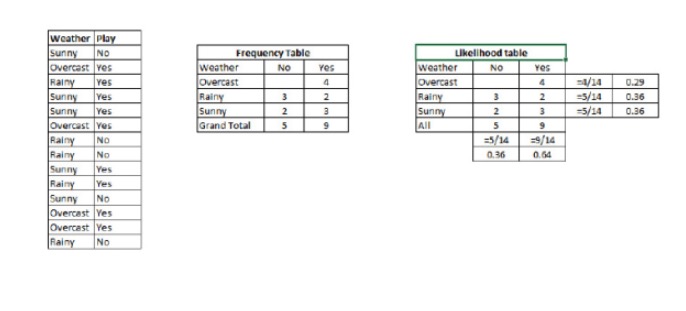
3단계: 이제, 단순 베이즈 방정식을 사용하여 각 클래스의 후진 확률을 계산한다. 후진 확률이 가장 큰 클래스는 예측된 결과이다.

질문: 참가자들은 날씨가 맑으면 게임을 할 수 있습니다.

이 문제를 풀기 위해 우리가 논의한 방법을 사용할 수 있습니다. 그래서 P (Play) = P (Play) / P (Play)

P가 있습니다. ³⁄₉ = 0.33, P는 ⁵⁄₁₄ = 0.36, P는 ⁹⁄₁₄ = 0.64.

이제 P는 0.33 * 0.64 / 0.36 = 0.60 입니다.

순진한 베이스 (Prudent Bayes) 는 비슷한 방법을 사용하여 다른 속성을 통해 다른 범주의 확률을 예측한다. 이 알고리즘은 일반적으로 텍스트 분류와 여러 범주에 관련된 문제에 사용됩니다.

• #### 파이썬 코드:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)