1. 간략한 소개

최근 몇 년 동안 딥 뉴럴 네트워크는 점점 더 인기를 끌면서 다양한 분야에서 이전에는 해결할 수 없었던 문제를 해결하고 강력한 역량을 보여주고 있습니다. 시계열 예측에서 일반적으로 사용되는 신경망 가격은 RNN입니다. RNN은 현재 데이터 입력뿐만 아니라 과거 데이터 입력도 있기 때문입니다. 물론 RNN이 가격을 예측한다고 말할 때 우리는 종종 RNN 유형에 대해 이야기합니다. : LSTM . 이 글에서는 PyTorch를 기반으로 비트코인 ​​가격을 예측하는 모델을 구축하겠습니다. 인터넷에는 관련 정보가 많이 있지만 아직 충분히 철저하지 않고, pytorch를 사용하는 사람도 상대적으로 적습니다. 여전히 글을 써야 합니다. 최종 결과는 시가, 종가를 사용하는 것입니다. 비트코인 시장의 최고가, 최저가, 거래량을 파악하여 다음 종가를 예측합니다. 제가 신경망에 대해 아는 바는 보통 수준이고, 여러분의 비판과 수정을 환영합니다. 이 튜토리얼은 디지털 통화 양적 거래 플랫폼(www.fmz.com)의 발명가인 FMZ가 제작했습니다. QQ 그룹에 가입해 주셔서 감사합니다: 863946592로 연락해 주세요.

2. 데이터 및 참고문헌

관련 가격 예측 예: https://yq.aliyun.com/articles/538484 RNN 모델에 대한 자세한 소개: https://zhuanlan.zhihu.com/p/27485750 RNN의 입력 및 출력 이해: https://www.zhihu.com/question/41949741/answer/318771336 PyTorch에 대하여: 공식 문서 https://pytorch.org/docs 다른 정보는 직접 검색해 보세요. 이 외에도 이 글을 이해하려면 판다스/크롤러/데이터 처리 등의 사전 지식이 필요한데, 몰라도 상관없습니다.

3. PyTorch LSTM 모델의 매개변수

LSTM의 매개변수:

처음 문서에서 이렇게 밀집되어 있는 매개변수를 봤을 때, 제 반응은 다음과 같았습니다. 천천히 읽어 내려가다가 마침내 이해하게 되었습니다.

input_size: 입력 벡터 x의 특징 크기. 종가를 사용하여 종가를 예측하는 경우 input_size=1입니다. 종가를 시가와 종가로 예측하는 경우 input_size=4입니다. hidden_size: 숨겨진 레이어 크기 num_layers: RNN의 레이어 수 batch_first: True이면 첫 번째 입력 차원은 batch_size입니다. 이 매개변수도 매우 혼란스럽고 아래에서 자세히 설명합니다.

입력 데이터 매개변수:

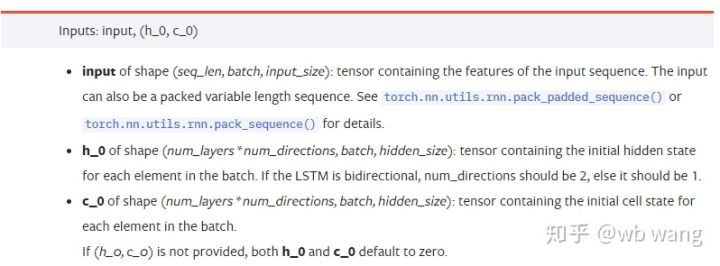
input: 특정 입력 데이터는 (seq_len, batch, input_size)의 특정 모양을 갖는 3차원 텐서입니다. 그 중 seq_len은 시퀀스의 길이, 즉 LSTM이 과거 데이터를 고려해야 하는 길이를 나타냅니다. 이는 LSTM의 내부 구조가 아닌 데이터 형식에만 해당합니다. 동일한 LSTM 모델은 seq_len이 다른 입력 데이터이며 예측을 제공할 수 있습니다. 결과; 배치는 배치 크기를 나타내며, 이는 서로 다른 데이터 그룹의 수를 나타냅니다. 입력 크기는 이전 입력 크기입니다. h_0: 초기 숨겨진 상태, 모양은 (num_layers * num_directions, batch, hidden_size)이고, 양방향 네트워크인 경우 num_directions=2입니다. c_0: 초기 셀 상태, 모양은 위와 동일하며, 지정하지 않아도 됩니다.

출력 매개변수:

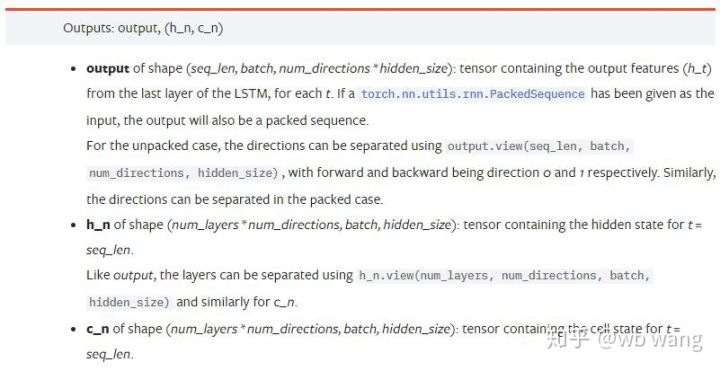
output: 출력 모양(seq_len, batch, num_directions * hidden_size), 이는 모델 매개변수 batch_first와 관련되어 있다는 점에 유의하세요. h_n: 시간 t = seq_len에서의 h 상태, h_0와 동일한 모양 c_n: t = seq_len 시점의 c 상태, c_0와 동일한 모양

4. LSTM 입력 및 출력의 간단한 예

먼저 필요한 패키지를 가져옵니다.

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

LSTM 모델 정의

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

입력 데이터 준비

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

x의 모양은 (3,4,5)입니다.batch_first=True이때 batch_size는 3, sqe_len은 4, input_size는 5입니다. 엑스[0]은 첫 번째 배치를 나타냅니다.

batch_first가 정의되지 않으면 False가 기본값으로 설정되고, 데이터는 배치 크기가 4, sqe_len이 3, input_size가 5로 완전히 다르게 표현됩니다. 이 때 x[0]은 t=0에서의 모든 배치의 데이터를 나타냅니다. 개인적으로 이 설정이 직관적이지 않다고 생각해서 매개변수를 추가했습니다.batch_first=True.

두 가지 사이의 데이터 변환도 매우 편리합니다.x.permute(1,0,2)

입력 및 출력

LSTM의 입력과 출력 형태는 혼동되기 쉽습니다. 다음 그림을 통해 이해해 보세요.
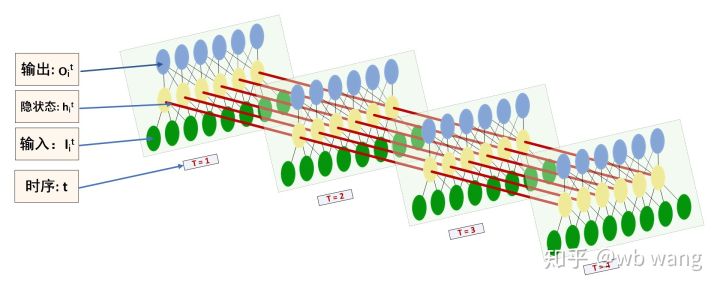
출처: https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

이전 매개변수 설명과 일치하는 출력 결과를 관찰합니다. hn.size()의 두 번째 값은 3이며, 이는 batch_size의 크기와 일치합니다. 즉, hn에는 중간 상태가 저장되지 않고 마지막 단계만 저장된다는 것을 나타냅니다. LSTM 네트워크에는 두 개의 레이어가 있으므로 hn의 마지막 레이어의 출력은 실제로 출력의 값이며 출력의 모양은 다음과 같습니다.[3, 4, 10]은 모든 순간 t=0,1,2,3의 결과를 저장하므로:

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. 비트코인 ​​시장 데이터 준비

제가 이전에 말한 것의 대부분은 서론일 뿐입니다. LSTM의 입력과 출력을 이해하는 것이 매우 중요합니다. 그렇지 않으면 인터넷에서 무작위로 일부 코드를 복사하면 실수를 하기 쉽습니다. 강력한 능력으로 인해 LSTM은 시계열에서, 모델이 틀렸더라도 결국에는 얻을 수 있습니다. 좋은 결과입니다.

데이터 수집

사용된 데이터는 Bitfinex 거래소의 BTC_USD 거래 쌍에 대한 시장 데이터입니다.

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

데이터 형식은 다음과 같습니다.

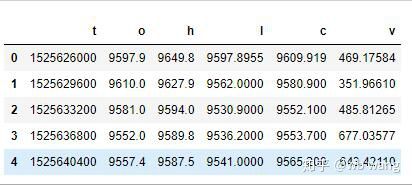
데이터 전처리

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

데이터 표준화 방법은 매우 거칠고 몇 가지 문제가 있을 것입니다. 그것은 단지 시범을 위한 것입니다. 수율과 같은 데이터 표준화를 사용할 수 있습니다.

훈련 데이터 준비

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

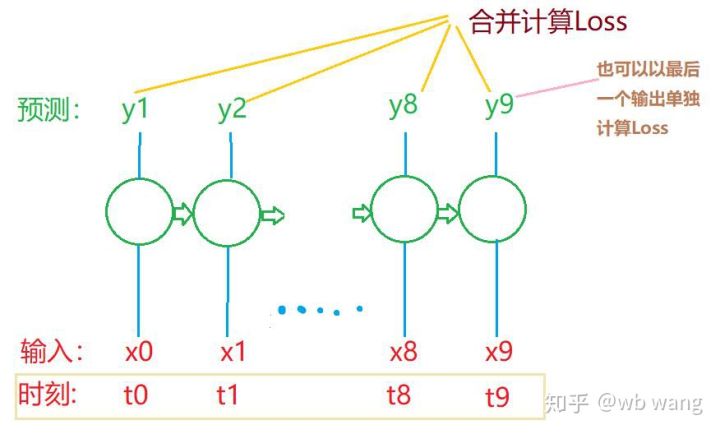
train_x와 train_y의 최종 모양은 다음과 같습니다. torch.Size([800, 10, 5]), torch.Size([800, 10, 1]). 우리 모델은 10개 기간의 데이터를 기반으로 다음 기간의 종가를 예측하므로 이론적으로 800개 배치에는 800개의 예측 종가만 필요합니다. 하지만 train_y는 각 배치에 10개의 데이터를 가지고 있습니다. 사실, 각 배치 예측의 중간 결과는 마지막 결과만이 아니라 유지됩니다. 최종 손실을 계산할 때 10개의 예측 결과를 모두 고려하여 train_y의 실제 값과 비교할 수 있습니다. 이론적으로는 마지막 예측 결과의 손실만 계산하는 것도 가능합니다. 이 문제를 설명하기 위해 대략적인 다이어그램을 그렸습니다. LSTM 모델은 실제로 seq_len 매개변수를 포함하지 않기 때문에 모델을 다른 길이에 적용할 수 있으며, 중간 예측 결과도 의미가 있기 때문에 Loss 계산을 병합하는 경향이 있습니다.

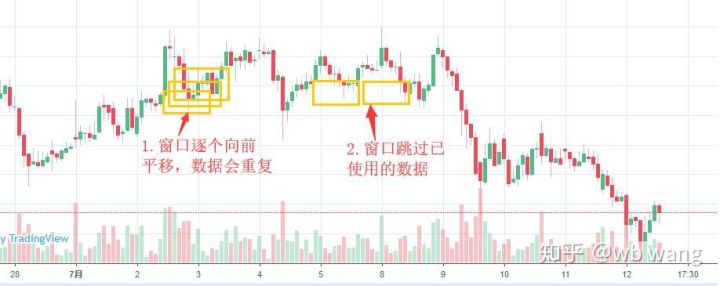
학습 데이터를 준비할 때 윈도우의 움직임이 불규칙하고, 사용된 데이터는 더 이상 사용되지 않는다는 점에 유의하세요. 물론 윈도우를 하나씩 이동할 수도 있으므로 얻은 학습 세트가 훨씬 더 커질 것입니다. . 하지만 인접한 배치 데이터가 너무 반복적이라고 느껴져서 지금의 방식을 채택하게 되었습니다.

6. LSTM 모델 구성

최종 모델은 다음과 같습니다. 여기에는 2개 레이어의 LSTM과 선형 레이어가 포함됩니다.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. 모델 학습 시작

마침내 훈련을 시작했는데 코드는 다음과 같습니다.

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
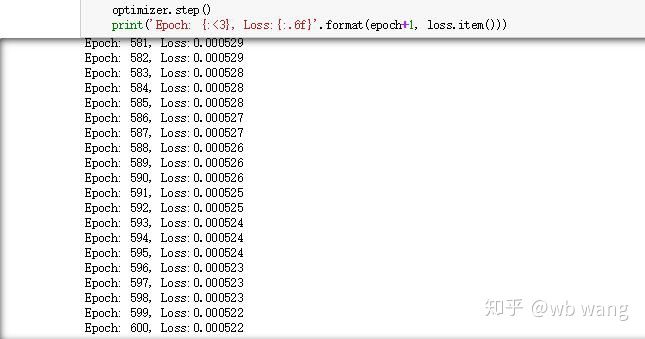
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

훈련 결과는 다음과 같습니다.

8. 모델 평가

모델의 예측 값은 다음과 같습니다.

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

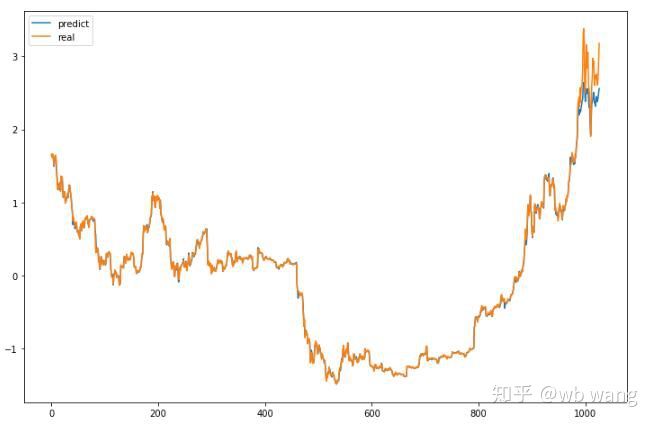
그림에서 볼 수 있듯이 학습데이터(800 이전)의 적합도는 매우 높지만 비트코인 ​​가격이 나중에 새로운 최고가로 상승했고 모델이 이러한 데이터를 보지 못했기 때문에 예측은 좋은 성과를 낼 수 없음. 이는 또한 이전의 데이터 표준화에 문제가 있었음을 보여줍니다. 예측된 가격이 정확하지 않을 수 있지만, 상승과 하락 예측은 얼마나 정확할까요? 예측 데이터의 일부를 살펴보세요.

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

상승 및 하락을 예측하는 정확도는 81.4%에 도달했는데, 이는 제가 기대했던 것보다 높은 수치입니다. 내가 어딘가 실수를 했는지 모르겠어요.

물론 이 모델은 실제 가치가 없지만 간단하고 이해하기 쉽습니다. 이것을 시작점으로 삼으세요. 디지털 통화 양적화에 신경망을 적용하는 것에 대한 입문 과정이 더 많이 있을 것입니다.