Aplicação Python Naive Bayes

Em termos mais simples, um classificador básico simples assume que uma característica da classificação não está relacionada com outras características da mesma. Por exemplo, se uma fruta é redonda e redonda, e tem cerca de 3 polegadas de diâmetro, então a fruta pode ser uma maçã. Mesmo que essas características dependam umas das outras, ou dependam de outras características, o classificador básico simples assume que essas características indicam que a fruta é uma maçã.

• #### Os modelos simples de Bayes são fáceis de construir e são muito úteis para grandes conjuntos de dados. Embora simples, o desempenho de Bayes simples ultrapassa métodos de classificação muito complexos.

O teorema de Bayes fornece uma forma de calcular a probabilidade de retorno P © {\displaystyle P © } a partir de P © {\displaystyle P © } , P (x) {\displaystyle P (x) } e P (x) {\displaystyle P (x) } . Veja a seguinte equação:

Aqui, não há nada de novo.

P © {\displaystyle \sigma © } é a probabilidade de retrospecção da classe (objectivo) assumindo que a variável de previsão (propriedade) {\displaystyle (property) } é conhecida P © é a probabilidade anterior da classe P (x) {\displaystyle \sigma (x) } é a probabilidade, isto é, a probabilidade de prever uma variável com uma classe conhecida. P (x) é a probabilidade anterior da variável de previsão Exemplo: Vamos entender o conceito com um exemplo. Abaixo, eu tenho um conjunto de treino para o tempo e a correspondente variável alvo Play. Agora, precisamos classificar os participantes que vão jogar e os que não vão jogar de acordo com o tempo. Vamos executar os seguintes passos.

Passo 1: Converter o conjunto de dados para uma tabela de frequências.

Passo 2: Criar uma tabela de likelihood usando uma probabilidade de jogar de 0,64 com uma probabilidade de Overcast de 0,29 para um jogo similar.

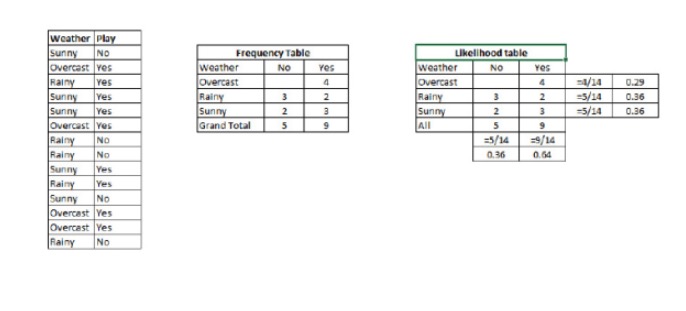
Passo 3: Agora, use a equação básica de Bayes para calcular a probabilidade de retorno de cada classe. A classe com maior probabilidade de retorno é o resultado previsto.

Pergunta: Se o tempo estiver bom, os participantes poderão jogar.

Podemos usar o método que discutimos para resolver este problema. Então, P (brincadeira) = P (brincadeira) * P (brincadeira) / P (brincadeira).

Então temos P = ³⁄₉ = 0,33, P = ⁵⁄₁₄ = 0,36, P = ⁹⁄₁₄ = 0,64.

Agora, a probabilidade de que P (Jogar) seja igual a 0,33 * 0,64 / 0,36 = 0,60 é maior.

O simplório Bayes usou um método semelhante para prever a probabilidade de diferentes categorias por meio de diferentes atributos. Este algoritmo é normalmente usado para classificação de texto, bem como para problemas envolvendo várias categorias.

• #### Código Python:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)