Наивное байесовское приложение Python

Если предположить, что переменные независимы друг от друга, то можно получить классификацию, основанную на теореме Бейеса. Говоря проще, классификатор Бейеса предполагает, что одно свойство классификации не связано с другими свойствами классификации. Например, если фрукт круглый, красный и диаметром около 3 дюймов, то это может быть яблоко. Даже если эти свойства зависят друг от друга или зависят от других свойств, классификатор Бейеса предполагает, что эти свойства независимо указывают на то, что фрукт является яблоком.

• #### Простая бейесовская модель легко построена и очень полезна для больших наборов данных. Хотя она проста, она выходит за рамки очень сложных методов классификации.

Теорема Бейеса дает способ вычислить вероятность P © {\displaystyle P © } послепроверки из P © {\displaystyle P © } , P (x) {\displaystyle P (x) } и P (x) {\displaystyle P (x) } . Обратите внимание на следующее уравнение:

Здесь, в Сирии,

P © {\displaystyle \sigma © } - вероятность последующего исхода класса (цель) при известном предсказуемом переменном (свойстве) {\displaystyle (\sigma © } P © - предыдущая вероятность класса P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn Mikä on todennäköisyys, joka ennustaa muuttujan, jos se on tunnettu P (x) - предварительная вероятность прогнозируемой переменной Пример: давайте разберем эту концепцию на примере. Ниже у меня есть тренировочный набор с погодой и соответствующая целевая переменная Play. Теперь нам нужно классифицировать участников, которые будут играть и не будут играть, в зависимости от погоды. Давайте выполним следующие шаги:

Шаг 1: Преобразование набора данных в таблицу частот.

Шаг 2: Создать таблицу вероятности, используя аналогичную таблицу, где вероятность Overcast равна 0.29, а вероятность игры равна 0.64.

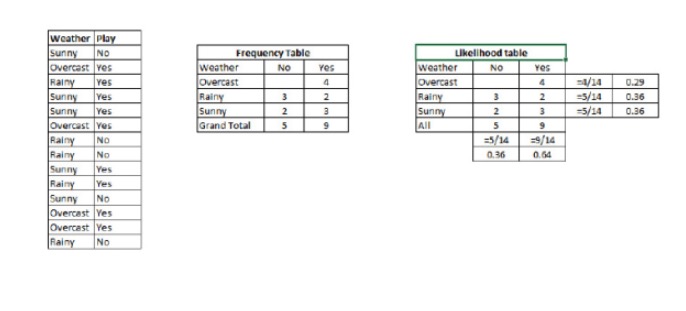
Шаг 3: Теперь, используя простое Бейесово уравнение, вычислим обратную вероятность для каждого класса. Класс с наибольшей обратной вероятностью - это результат прогноза.

Вопрос: Правильно ли это утверждение?

Мы можем решить эту задачу, используя метод, который мы обсуждали. Итак, P (играет) = P (играет) * P (играет) / P (играет).

У нас есть P (светлый) = ³⁄₉ = 0.33, P (светлый) = ⁵⁄₁₄ = 0.36, P (светлый) = ⁹⁄₁₄ = 0.64.

Теперь, P{\displaystyle P} = 0.33 * 0.64 / 0.36 = 0.60, с большей вероятностью.

Аналогичным методом, используемым простым Бейесом, для прогнозирования вероятности различных категорий с помощью различных атрибутов. Этот алгоритм обычно используется для классификации текста, а также для задач, касающихся нескольких категорий.

• #### Код Python:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)