Мысли о стратегиях высокочастотной торговли (3)
 0
0
 2664
2664

В предыдущей статье я рассказал, как моделировать совокупный объем торговли, и кратко проанализировал явление ценового шока. В этой статье мы продолжим анализировать данные по торговым ордерам. За последние два дня YGG запустил контракты на основе Binance U, и цена сильно колебалась. Объем торгов даже превысил BTC в какой-то момент. Давайте проанализируем это сегодня.
Интервал времени заказа
В общем, предполагается, что время поступления заказов следует процессу Пуассона. Вот статья, которая представляетпроцесс Пуассона . Я продемонстрирую это ниже.
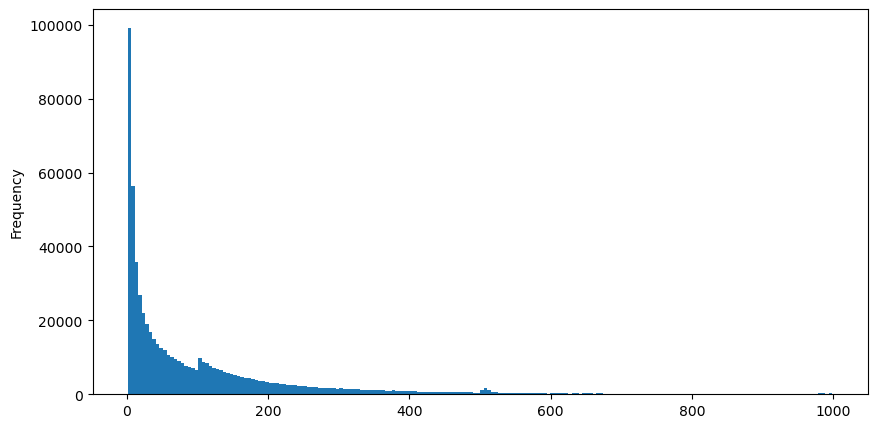
Загрузите aggTrades 5 августа, всего 1 931 193 сделки, что сильно преувеличено. Сначала давайте взглянем на распределение ордеров на покупку. Мы видим, что есть неравномерный локальный пик около 100 мс и 500 мс. Это должно быть вызвано запланированными ордерами, размещенными роботом, которому доверил Iceberg. Это также может быть одним о причинах, по которым рыночные условия в тот день были необычными.
Функция массы вероятности (PMF) распределения Пуассона определяется по формуле:
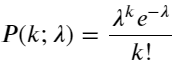
в:
- k — количество интересующих нас событий.
- λ — средняя частота возникновения событий в единицу времени (или единицу пространства).
- P(k; λ) — вероятность того, что произойдет ровно k событий, при средней частоте возникновения λ.
В процессе Пуассона временные интервалы между событиями распределены по экспоненциальному закону. Функция плотности вероятности (PDF) экспоненциального распределения определяется по формуле:
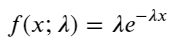
В результате подгонки было обнаружено, что результаты существенно отличаются от ожидаемых результатов распределения Пуассона. Процесс Пуассона недооценил частоту длинных интервалов и переоценил частоту коротких интервалов. (Фактическое распределение интервалов ближе к модифицированному распределению Парето)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
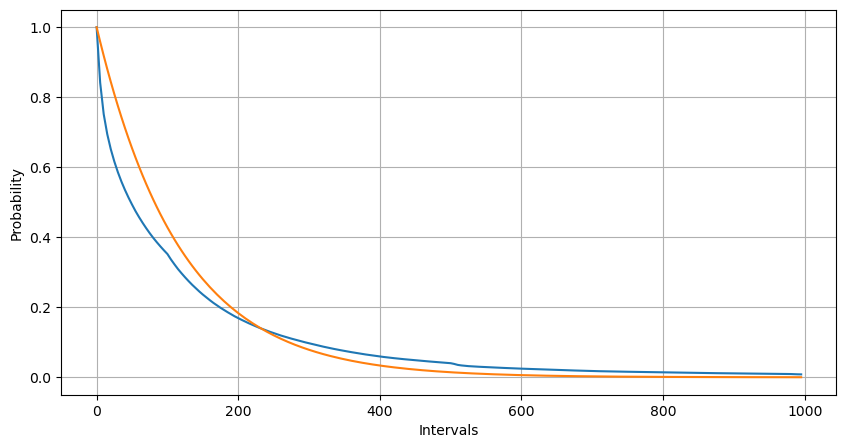
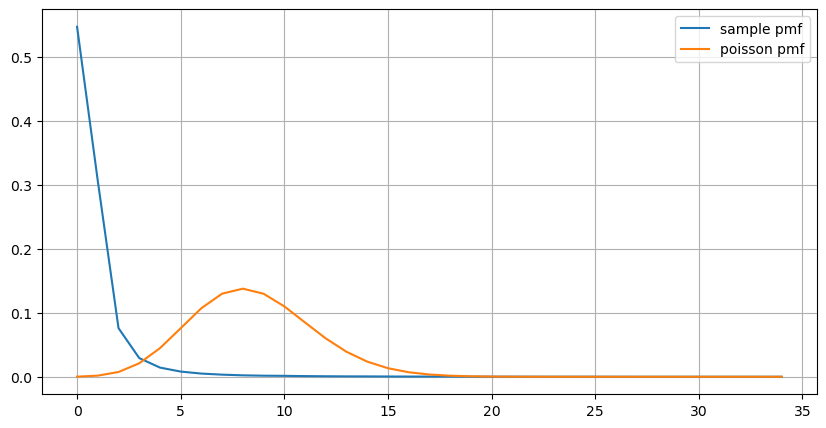
Статистическое распределение количества заказов, поступивших в течение 1 секунды, и сравнение с распределением Пуассона также показывают весьма очевидную разницу. Распределение Пуассона существенно недооценивает частоту маловероятных событий. Возможные причины:
- Непостоянная частота возникновения: процесс Пуассона предполагает, что средняя частота событий, происходящих в любой заданный период времени, постоянна. Если это предположение не выполняется, то распределение данных будет отклоняться от распределения Пуассона.
- Взаимодействие процессов: Еще одним основным предположением процесса Пуассона является то, что события независимы друг от друга. Если реальные события влияют друг на друга, их распределение может отклоняться от распределения Пуассона.
То есть в реальной среде частота заказов непостоянна, ее необходимо обновлять в режиме реального времени, и будут возникать стимулы, то есть большее количество заказов в фиксированное время будет стимулировать большее количество заказов. Это делает невозможным фиксацию хотя бы одного параметра в стратегии.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Параметры обновления в реальном времени
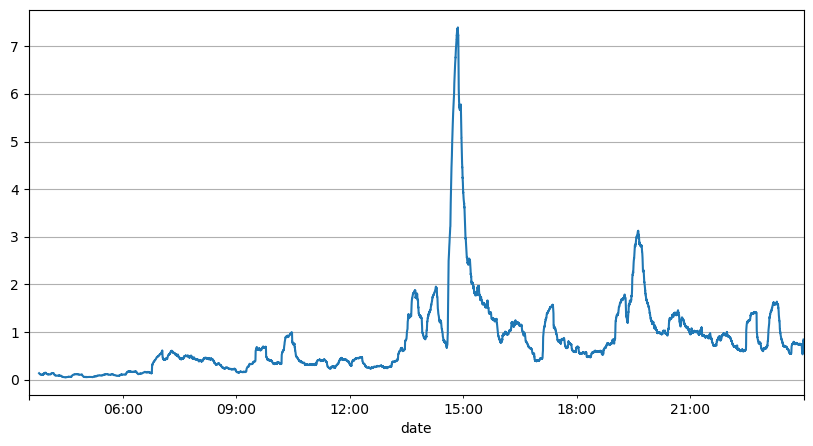
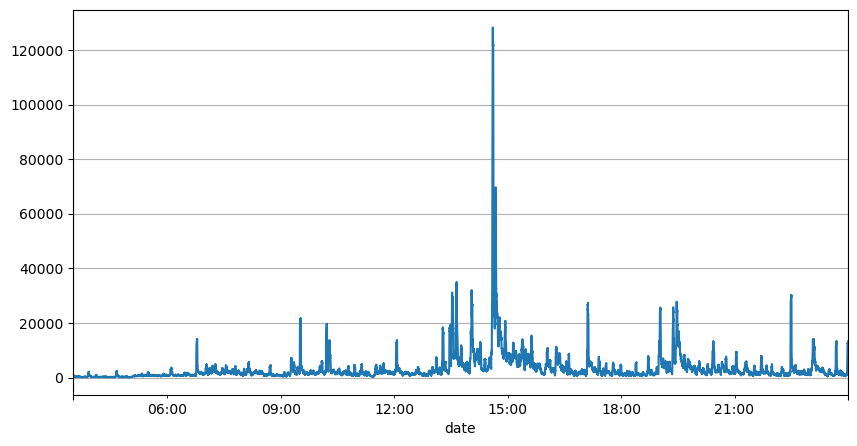
Предыдущий анализ интервалов ордеров показывает, что фиксированные параметры не подходят для реальных рыночных условий, а ключевые параметры рыночного описания стратегии необходимо обновлять в режиме реального времени. Самое простое решение — это скользящее среднее скользящего окна. Два рисунка ниже — это частота заказов на покупку в течение 1 секунды и среднее значение 1000 окон торгового объема. Видно, что в транзакциях наблюдается феномен кластеризации, то есть частота заказов значительно выше, чем обычно для период времени, и громкость в это время также увеличивается синхронно. Здесь предыдущее среднее значение используется для прогнозирования значения последней секунды, а средняя абсолютная ошибка остатка используется для измерения качества прогноза.
Из графика мы также можем понять, почему частота заказов так сильно отклоняется от распределения Пуассона. Хотя среднее число заказов в секунду составляет всего 8,5 раз, в экстремальных случаях среднее число заказов в секунду сильно отклоняется от него.
В результате было обнаружено, что использование среднего значения за предыдущие две секунды для прогнозирования остаточной ошибки является наименьшим и намного лучше, чем простой средний результат прогнозирования.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Подвести итог
В данной статье кратко рассматриваются причины, по которым временной интервал заказа отклоняется от процесса Пуассона, главным образом из-за того, что параметры изменяются со временем. Чтобы точнее прогнозировать рынок, стратегия должна делать прогнозы в режиме реального времени по основным параметрам рынка. Остатки можно использовать для измерения качества прогнозов. Приведенный выше пример является самым простым. Существует множество связанных исследований по анализу временных рядов, агрегации волатильности и т. д., которые можно улучшить.