1. Краткое введение

Глубокие нейронные сети в последние годы становятся все более популярными, решая ранее неразрешимые проблемы во многих областях и демонстрируя свои мощные возможности. При прогнозировании временных рядов обычно используемая цена нейронной сети — это RNN, поскольку RNN имеет не только текущие входные данные, но и исторические входные данные. Конечно, когда мы говорим о RNN, прогнозирующем цены, мы часто говорим о типе RNN : LSTM. В этой статье будет создана модель для прогнозирования цен на биткоины на основе pytorch. Хотя в Интернете много соответствующей информации, она все еще недостаточно полная, и сравнительно мало людей используют pytorch. Все равно необходимо написать статью. Конечный результат — использовать цену открытия, цену закрытия, самую высокую цену , самая низкая цена и объем транзакций на рынке биткоинов. для прогнозирования следующей цены закрытия. Мои личные познания в области нейронных сетей средние, и я буду рад вашей критике и исправлениям. Это руководство создано FMZ, изобретателем цифровой валютной количественной торговой платформы (www.fmz.com). Добро пожаловать в группу QQ: 863946592 для связи.

2. Данные и ссылки

Соответствующий пример прогнозирования цен: https://yq.aliyun.com/articles/538484 Подробное введение в модель RNN: https://zhuanlan.zhihu.com/p/27485750 Понимание ввода и вывода RNN: https://www.zhihu.com/question/41949741/answer/318771336 О pytorch: Официальная документация https://pytorch.org/docs Дополнительную информацию ищите самостоятельно. Кроме того, для понимания этой статьи необходимы некоторые предварительные знания, такие как pandas/crawlers/data processing и т. д., но неважно, если вы их не знаете.

3. Параметры модели LSTM pytorch

Параметры LSTM:

Когда я впервые увидел эти плотно упакованные параметры в документе, моей реакцией было: Читая медленно, я наконец понял.

input_size: Размер признака входного вектора x. Если цена закрытия используется для прогнозирования цены закрытия, то input_size=1; если цена закрытия прогнозируется по открытию максимума и закрытию минимума, то input_size=4 hidden_size: Размер скрытого слоя num_layers: Количество слоев RNN batch_first: Если True, то первым входным измерением является batch_size. Этот параметр также очень запутан и будет подробно описан ниже.

Параметры входных данных:

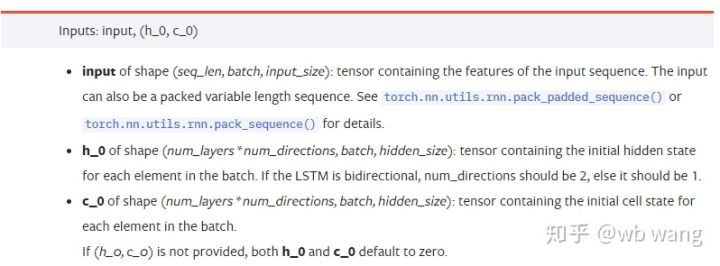
input: Конкретные входные данные представляют собой трехмерный тензор с определенной формой (seq_len, batch, input_size). Среди них seq_len относится к длине последовательности, то есть, как долго исторические данные LSTM должны учитываться. Обратите внимание, что это относится только к формату данных, а не к внутренней структуре LSTM. Та же самая модель LSTM может входные данные с разным seq_len и могут давать прогнозы. Результат; batch относится к размеру пакета, который представляет, сколько существует различных групп данных; input_size — это предыдущий input_size. h_0: Начальное скрытое состояние, форма — (num_layers * num_directions, batch, hidden_size), если это двунаправленная сеть, num_directions=2 c_0: Начальное состояние ячейки, форма та же, что и выше, можно не указывать.

Выходные параметры:

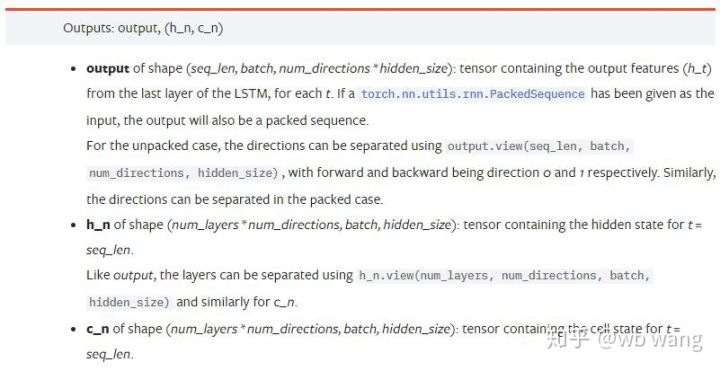
output: Выходная форма (seq_len, batch, num_directions * hidden_size), обратите внимание, что она связана с параметром модели batch_first h_n: состояние h в момент времени t = seq_len, та же форма, что и h_0 c_n: состояние c в момент времени t = seq_len, та же форма, что и c_0

4. Простой пример ввода и вывода LSTM

Сначала импортируйте необходимые пакеты.

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Определение модели LSTM

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Подготовка входных данных

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

Форма x — (3,4,5), поскольку мы определилиbatch_first=Trueв настоящее время batch_size равен 3, sqe_len равен 4, а input_size равен 5. х[0] представляет первую партию.

Если batch_first не определен, по умолчанию он равен False, и данные представляются совершенно иначе: размер пакета равен 4, sqe_len равен 3 и input_size равен 5. В это время х[0] представляет данные всех партий при t=0 и т. д. Лично я считаю, что эта настройка не интуитивно понятна, поэтому я добавил параметрbatch_first=True.

Преобразование данных между ними также очень удобно:x.permute(1,0,2)

Ввод и вывод

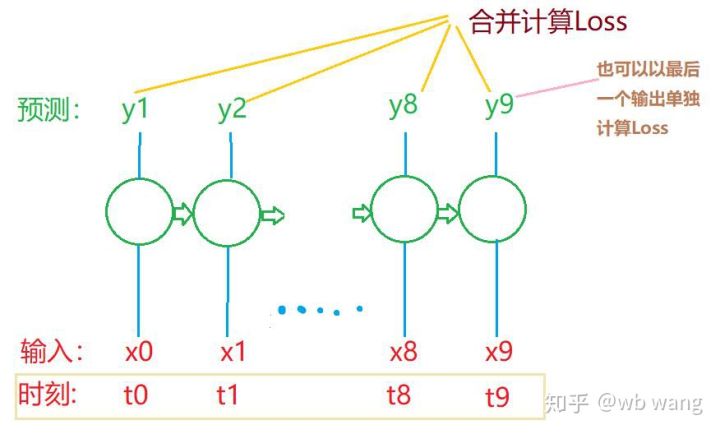
Форму входа и выхода LSTM легко спутать. Для понимания приведем следующий рисунок:
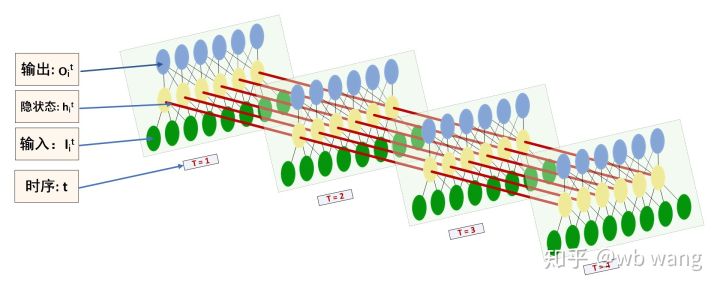
Источник: https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Обратите внимание на выходные результаты, которые согласуются с предыдущим объяснением параметров. Обратите внимание, что второе значение hn.size() равно 3, что соответствует размеру batch_size, указывая на то, что в hn не сохраняется промежуточное состояние, а сохраняется только последний шаг. Поскольку наша сеть LSTM имеет два слоя, выход последнего слоя hn на самом деле является значением выхода, а форма выхода —[3, 4, 10], сохраняет результаты всех моментов t=0,1,2,3, поэтому:

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Подготовьте данные по рынку биткоинов

Так много из того, что я сказал ранее, это всего лишь прелюдия. Очень важно понимать вход и выход LSTM. В противном случае легко ошибиться, если вы случайно скопируете некоторые коды из Интернета. Благодаря мощной способности LSTM во временных рядах, даже если модель неверна, в конце концов можно получить. Хорошие результаты.

Сбор данных

Используемые данные представляют собой рыночные данные торговой пары BTC_USD биржи Bitfinex.

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

Формат данных следующий:

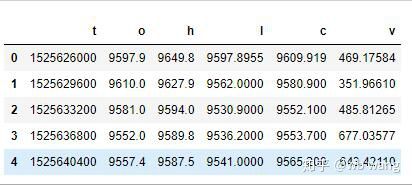
Предварительная обработка данных

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

Метод стандартизации данных очень грубый и будут некоторые проблемы. Он просто для демонстрации. Вы можете использовать стандартизацию данных, например yield.

Подготовка обучающих данных

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

Окончательные формы train_x и train_y: torch.Size([800, 10, 5]), torch.Size([800, 10, 1]). Поскольку наша модель прогнозирует цену закрытия следующего периода на основе данных за 10 периодов, теоретически для 800 партий требуется всего 800 прогнозируемых цен закрытия. Но train_y имеет 10 данных в каждой партии. Фактически, сохраняются промежуточные результаты каждого прогноза партии, а не только последний. При расчете окончательного Loss все 10 результатов прогнозирования могут быть учтены и сравнены с фактическими значениями в train_y. Теоретически также возможно рассчитать только убыток последнего результата прогноза. Я нарисовал примерную схему, чтобы проиллюстрировать эту проблему. Поскольку модель LSTM фактически не содержит параметра seq_len, модель можно применять к разным длинам, а промежуточные результаты прогнозирования также имеют смысл, поэтому я склонен объединять расчет потерь.

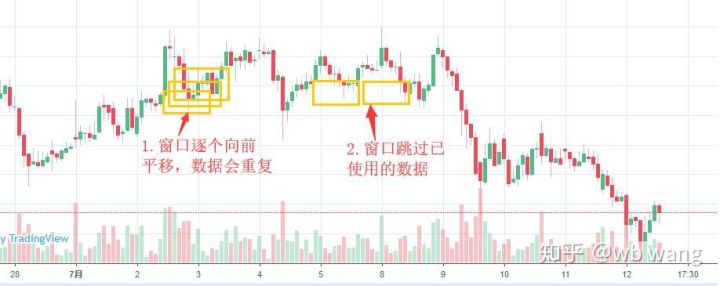
Обратите внимание, что при подготовке обучающих данных движение окна скачкообразно, и данные, которые были использованы, больше не используются. Конечно, окна также можно перемещать по одному, так что полученный обучающий набор будет намного больше . Но мне показалось, что данные смежного пакета слишком повторяются, поэтому я применил текущий метод.

6. Построение модели LSTM

Окончательная модель выглядит следующим образом: она включает двухслойную LSTM и линейный слой.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. Начните обучение модели.

Наконец-то начал обучение, код такой:

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Результаты обучения следующие:

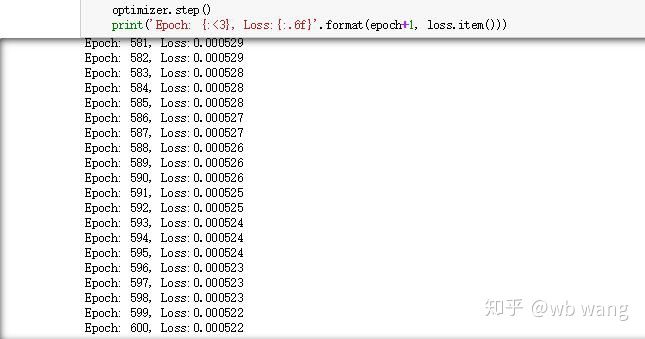
8. Оценка модели

Прогнозируемые значения модели:

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

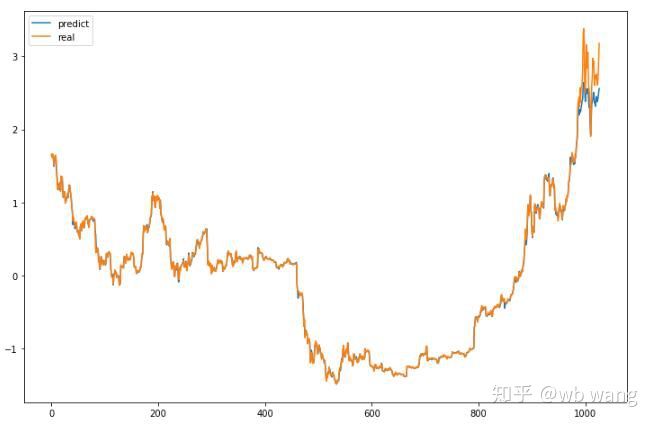
Как видно из рисунка, степень соответствия обучающих данных (до 800) очень высока, но цена биткоина позже выросла до нового максимума, и модель не увидела эти данные, поэтому прогноз неспособны хорошо выступить. Это также показывает, что в предыдущей стандартизации данных существовала проблема. Хотя прогнозируемая цена может быть неточной, насколько точным является прогноз роста и падения? Взгляните на часть данных прогноза:

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

Точность прогнозирования подъемов и падений достигла 81,4%, что превзошло мои ожидания. Не знаю, ошибся ли я где-то.

Конечно, эта модель не имеет реальной ценности, но она проста и легка для понимания. Просто используйте ее как отправную точку. Будут еще вводные курсы по применению нейронных сетей в количественной оценке цифровой валюты.