اعلی تعدد تجارتی حکمت عملی کے بارے میں خیالات (3)
 0
0
 2664
2664

پچھلے مضمون میں، میں نے مجموعی تجارتی حجم کو ماڈل بنانے کا طریقہ متعارف کرایا اور قیمت کے جھٹکے کے رجحان کا مختصراً تجزیہ کیا۔ یہ مضمون تجارت کے آرڈر کے ڈیٹا کا تجزیہ کرتا رہے گا۔ پچھلے دو دنوں میں، YGG نے Binance U پر مبنی معاہدے شروع کیے، اور قیمت میں بہت زیادہ اتار چڑھاؤ آیا، اور تجارتی حجم ایک وقت پر BTC سے بھی بڑھ گیا، آئیے آج اس کا تجزیہ کرتے ہیں۔
آرڈر ٹائم وقفہ
عام طور پر، یہ فرض کیا جاتا ہے کہ جب آرڈرز آتے ہیں تو ایک پوسن کے عمل کے بعد یہاں ایک مضمون پیش کیا جاتا ہے۔زہر کا عمل . میں ذیل میں اس کا مظاہرہ کروں گا۔
5 اگست کو aggTrades ڈاؤن لوڈ کریں، مجموعی طور پر 1,931,193 ٹریڈز ہیں، جو کہ کافی مبالغہ آمیز ہے۔ سب سے پہلے، آئیے خرید آرڈرز کی تقسیم پر ایک نظر ڈالتے ہیں کہ تقریباً 100ms اور 500ms پر ایک غیر مساوی چوٹی ہے جو کہ Iceberg کے ذریعے سونپے گئے مقررہ آرڈرز کی وجہ سے ہو سکتی ہے۔ ان وجوہات میں سے کیوں کہ اس دن مارکیٹ کے حالات غیر معمولی تھے۔
Poisson کی تقسیم کا امکانی ماس فنکشن (PMF) بذریعہ دیا گیا ہے:
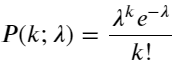
میں:
- k وہ واقعات کی تعداد ہے جس میں ہماری دلچسپی ہے۔
- λ فی یونٹ وقت (یا یونٹ کی جگہ) کے واقعات کی اوسط وقوع کی شرح ہے۔
- P(k؛ λ) واقع ہونے کی اوسط شرح λ کے پیش نظر، بالکل k کے واقعات کا امکان ہے۔
Poisson کے عمل میں، واقعات کے درمیان وقت کے وقفے ایک کفایتی تقسیم کی پیروی کرتے ہیں۔ کفایتی تقسیم کا امکانی کثافت فنکشن (PDF) بذریعہ دیا گیا ہے:
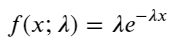
فٹنگ کے ذریعے، یہ پایا گیا کہ نتائج پوسن کی تقسیم کے متوقع نتائج سے کافی مختلف تھے، پوسن کے عمل نے طویل وقفوں کی تعدد کو کم کیا اور مختصر وقفوں کی تعدد کو بڑھاوا دیا۔ (اصل وقفہ کی تقسیم ترمیم شدہ پیریٹو تقسیم کے قریب ہے)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
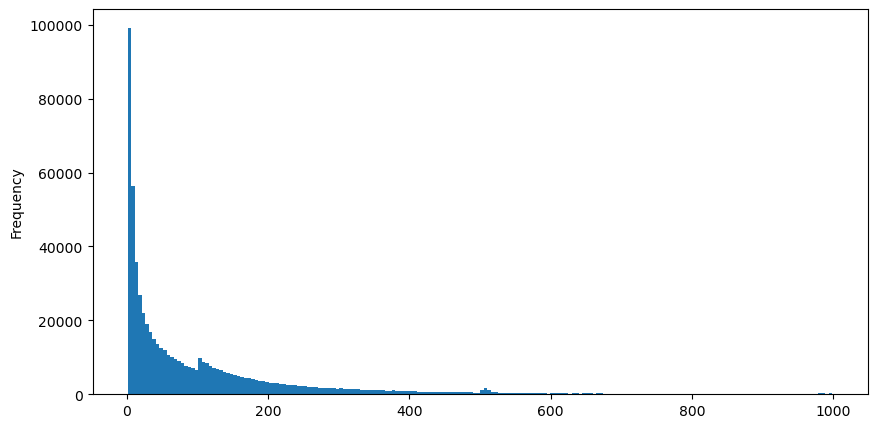
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
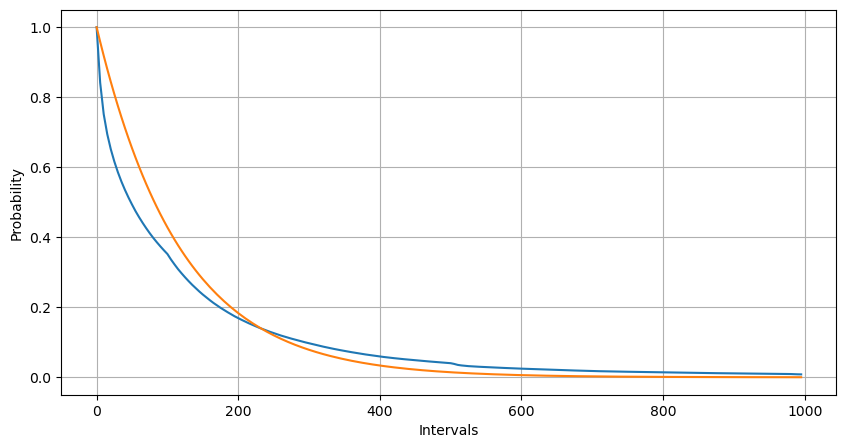
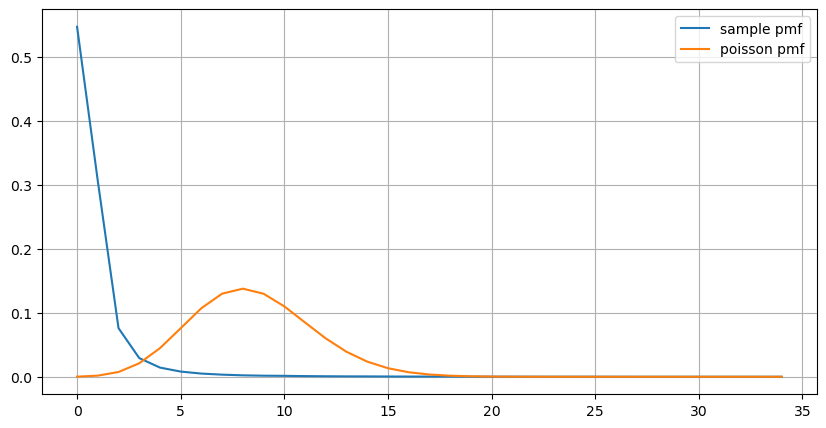
آرڈرز کی تعداد کی شماریاتی تقسیم جو 1 سیکنڈ کے اندر ہوتی ہے اور پوسن کی تقسیم سے موازنہ بھی بہت واضح فرق ظاہر کرتا ہے۔ پوسن کی تقسیم کم امکانی واقعات کی تعدد کو نمایاں طور پر کم کرتی ہے۔ ممکنہ وجوہات:
- وقوع کی غیر مستقل شرح: Poisson عمل یہ فرض کرتا ہے کہ کسی بھی مدت میں رونما ہونے والے واقعات کی اوسط شرح مستقل ہے۔ اگر یہ مفروضہ برقرار نہیں رہتا ہے، تو ڈیٹا کی تقسیم Poisson کی تقسیم سے ہٹ جائے گی۔
- عمل کا تعامل: Poisson کے عمل کا ایک اور بنیادی مفروضہ یہ ہے کہ واقعات ایک دوسرے سے آزاد ہیں۔ اگر حقیقی دنیا کے واقعات ایک دوسرے پر اثر انداز ہوتے ہیں، تو ان کی تقسیم Poisson کی تقسیم سے ہٹ سکتی ہے۔
کہنے کا مطلب یہ ہے کہ، ایک حقیقی ماحول میں، آرڈرز کی فریکوئنسی غیر مستقل ہوتی ہے، اسے حقیقی وقت میں اپ ڈیٹ کرنے کی ضرورت ہوتی ہے، اور مراعات ملیں گی، یعنی ایک مقررہ وقت میں زیادہ آرڈرز زیادہ آرڈرز کو متحرک کریں گے۔ اس سے حکمت عملی میں کسی ایک پیرامیٹر کو ٹھیک کرنا ناممکن ہو جاتا ہے۔
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
ریئل ٹائم اپ ڈیٹ کے پیرامیٹرز
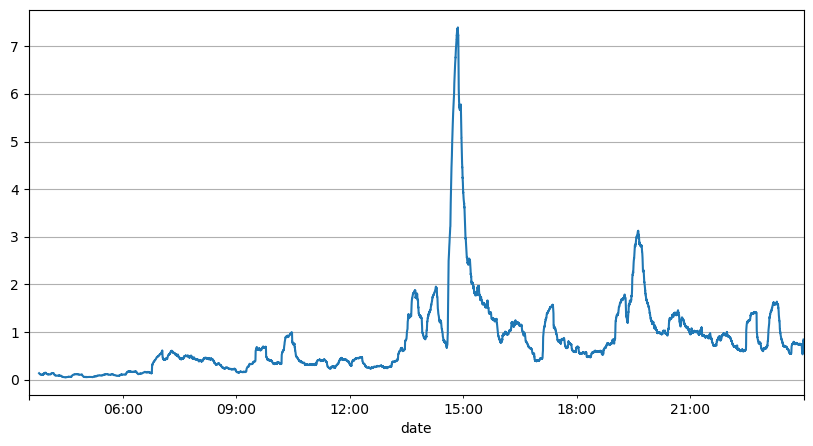
آرڈر کے وقفوں کے پچھلے تجزیے سے پتہ چلتا ہے کہ فکسڈ پیرامیٹرز حقیقی مارکیٹ کے حالات کے لیے موزوں نہیں ہیں، اور حکمت عملی کی مارکیٹ کی تفصیل کے اہم پیرامیٹرز کو حقیقی وقت میں اپ ڈیٹ کرنے کی ضرورت ہے۔ سوچنے کا سب سے آسان حل سلائیڈنگ ونڈو کی متحرک اوسط ہے۔ نیچے دیے گئے دو اعداد و شمار 1 سیکنڈ کے اندر خریداری کے آرڈرز اور ٹریڈنگ والیوم کی اوسط 1000 ونڈوز ہیں، یہ دیکھا جا سکتا ہے کہ لین دین میں کلسٹرنگ کا رجحان ہے، یعنی آرڈرز کی فریکوئنسی ایک کے لیے معمول سے زیادہ ہے۔ وقت کی مدت، اور اس وقت حجم بھی ہم آہنگی سے بڑھتا ہے۔ یہاں، پچھلے وسط کو تازہ ترین سیکنڈ کی قدر کی پیشین گوئی کرنے کے لیے استعمال کیا جاتا ہے، اور بقایا کی اوسط مطلق غلطی پیشین گوئی کے معیار کی پیمائش کے لیے استعمال ہوتی ہے۔
گراف سے، ہم یہ بھی سمجھ سکتے ہیں کہ آرڈر فریکوئنسی Poisson کی تقسیم سے اتنی زیادہ انحراف کیوں کرتی ہے، حالانکہ فی سیکنڈ آرڈرز کی اوسط تعداد صرف 8.5 گنا ہے، انتہائی صورتوں میں آرڈرز کی اوسط تعداد اس سے بہت دور ہوتی ہے۔
یہاں یہ پایا جاتا ہے کہ بقایا غلطی کی پیشین گوئی کرنے کے لیے پچھلے دو سیکنڈز کا اوسط استعمال کرنا سب سے چھوٹا ہے اور سادہ اوسط پیشین گوئی کے نتیجے سے بہت بہتر ہے۔
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
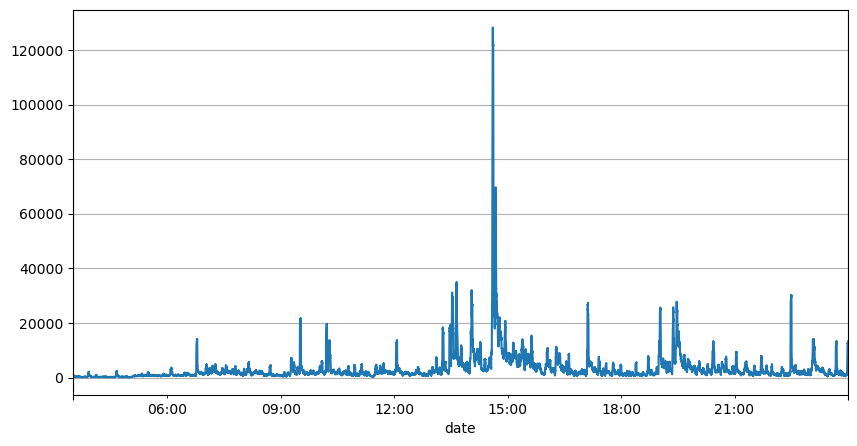
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
خلاصہ کریں۔
اس مضمون میں مختصراً ان وجوہات کا تعارف کرایا گیا ہے جن کی وجہ سے آرڈر ٹائم وقفہ پوسن کے عمل سے ہٹ جاتا ہے، بنیادی طور پر اس وجہ سے کہ وقت کے ساتھ ساتھ پیرامیٹرز تبدیل ہوتے رہتے ہیں۔ مارکیٹ کی زیادہ درست پیشین گوئی کرنے کے لیے، حکمت عملی کو مارکیٹ کے بنیادی پیرامیٹرز پر حقیقی وقت کی پیشین گوئیاں کرنے کی ضرورت ہے۔ باقیات کا استعمال پیشین گوئیوں کے معیار کی پیمائش کے لیے کیا جا سکتا ہے۔