بیز - احتمال کا راز کھولنا، فیصلے کرنے کے پیچھے ریاضی کی حکمت کی تلاش

بیزین شماریات ریاضی کے میدان میں ایک طاقتور نظم و ضبط ہے ، جس میں مالی ، طبی تحقیق اور انفارمیشن ٹکنالوجی سمیت بہت سارے شعبوں میں وسیع پیمانے پر اطلاق ہوتا ہے۔ یہ ہمیں نئے بعد کے عقائد اخذ کرنے کے لئے سابقہ عقائد کو شواہد کے ساتھ جوڑنے کی اجازت دیتا ہے ، جس سے ہمیں بہتر فیصلے کرنے میں مدد ملتی ہے۔

اس مضمون میں، ہم مختصر طور پر اس شعبے کے بانی اہم ریاضی دانوں میں سے کچھ متعارف کروائیں گے.

بیز سے پہلے بایزین شماریات کو بہتر طور پر سمجھنے کے لیے ہمیں 18 ویں صدی میں واپس جانا ہوگا اور ریاضی دان ڈی موئیر اور ان کے مقالے The Doctrine of Chances کا حوالہ دینا ہوگا۔

اپنے مقالے میں ، ڈی موئیر نے اپنے دور میں امکانات اور جوئے سے متعلق بہت سے مسائل حل کیے۔ جیسا کہ آپ کو معلوم ہوگا ، ان میں سے ایک مسئلے کے حل سے نارمل تقسیم کی ابتدا ہوئی ، لیکن یہ ایک اور کہانی ہے۔

اس کے کاغذ میں سب سے آسان سوالات میں سے ایک تھا:

ایک منصفانہ سکے کو تین بار لگاتار پھینکنے پر تین سر نکلنے کا کیا امکان ہے؟

The Doctrine of Chances میں بیان کردہ مسائل کو پڑھتے ہوئے ، آپ کو یہ معلوم ہوسکتا ہے کہ زیادہ تر ایک مفروضے سے شروع ہوتے ہیں جس سے وہ دیئے گئے واقعات کے لئے امکانات کا حساب لگاتے ہیں۔ مثال کے طور پر ، مذکورہ بالا سوال میں ایک مفروضہ ہے جو سکے کو منصفانہ سمجھتا ہے۔ لہذا ، ٹارش کے دوران ہیڈ حاصل کرنے کا امکان 0.5 ہے۔

یہ آج ریاضی کے لحاظ سے یوں بیان کیا جائے گا:

فارمولا

𝑃(𝑋|𝜃)

تاہم، اگر ہم نہیں جانتے کہ سکہ منصفانہ ہے یا نہیں؟𝜃 ?

تھامس بیز اور رچرڈ پرائس

تقریبا پچاس سال بعد ، 1763 میں ، لندن کی رائل سوسائٹی کے فلسفیانہ لین دین میں ایک حل نامی ایک کاغذ شائع ہوا۔

اس دستاویز کے پہلے چند صفحات میں ، ریاضی دان رچرڈ پرائس کا ایک ٹکڑا لکھا گیا ہے جو اس کے دوست تھامس بیز نے اپنی موت سے کئی سال قبل لکھا تھا اس کا خلاصہ کرتا ہے۔ اپنے تعارف میں ، پرائس نے تھامس بیز کی طرف سے کی جانے والی کچھ اہم دریافتوں کی وضاحت کی جو ڈی موئیر کے دکترین آف چانسز میں ذکر نہیں کی گئیں۔

دراصل، اس نے ایک خاص مسئلے کا ذکر کیا:

ایک نامعلوم واقعہ کی کامیابیوں اور ناکامیوں کی تعداد کے پیش نظر، دو نامعلوم ڈگریوں کے درمیان اس کا موقع تلاش کریں۔

دوسرے الفاظ میں، ایک واقعہ کا مشاہدہ کرنے کے بعد ہم اس بات کا تعین کیا ہے کہ نامعلوم پیرامیٹر کا امکان کیا ہےθدو ڈگری کے درمیان آتا ہے. یہ اصل میں تاریخ میں شماریاتی نتیجہ اخذ کرنے سے متعلق پہلے مسائل میں سے ایک ہے اور اس نے اصطلاح الٹا امکان کو جنم دیا. ریاضی کے لحاظ سے:

فارمولا

𝑃( 𝜃 | 𝑋）

یہ ہے کہ ہم آج Bayes نظریہ کے پیچھے کی تقسیم کو بلاتے ہیں.

کسی وجہ اور اثر کے بغیر

ان دو بزرگ وزراء کی تحقیق کے پیچھے حوصلہ افزائی کو سمجھنے،تھامس بیزاوررچرڈ پرائسلیکن ایسا کرنے کے لئے، ہمیں عارضی طور پر اعداد و شمار کے بارے میں کچھ علم کو ایک طرف رکھنے کی ضرورت ہے۔

ہم 18 ویں صدی میں ہیں جب ریاضی دانوں کے لئے احتمال ایک بڑھتا ہوا دلچسپ شعبہ بن رہا ہے۔ ڈی موئیر یا برنولی جیسے ریاضی دانوں نے پہلے ہی دکھایا ہے کہ کچھ واقعات کسی حد تک بے ترتیب کے ساتھ ہوتے ہیں لیکن پھر بھی مقررہ قوانین کے تحت چلتے ہیں۔ مثال کے طور پر ، اگر آپ کئی بار ڈاس پھینکتے ہیں تو ، اس وقت کا چھٹا حصہ چھ پر اترے گا۔ یہ ایسا ہی ہے جیسے کوئی پوشیدہ اصول ہے جو قسمت کے امکانات کا تعین کرتا ہے۔

اب ذرا تصور کریں کہ آپ اس دور میں رہنے والے ایک ریاضی دان اور عقیدت مند ہیں۔ آپ کو اس پوشیدہ اصول اور خدا کے درمیان تعلقات کو سمجھنے میں دلچسپی ہو سکتی ہے۔

یہ دراصل خود بیز اور پرائس نے یہ سوال کیا تھا۔ انہیں امید تھی کہ ان کا حل براہ راست ثابت کرنے پر لاگو ہوگا کہ دنیا کو حکمت اور ذہانت کا نتیجہ ہونا ضروری ہے۔ اس طرح خدا کے وجود کے لئے ثبوت فراہم کرنا حتمی وجہ کے طور پر - یعنی وجہ کے بغیر وجہ۔

لیپلاس

حیرت کی بات یہ ہے کہ تقریبا دو سال بعد 1774 میں ، تھامس بیز کے کاغذ کو پڑھنے کے بغیر ، فرانسیسی ریاضی دان لیپلاس نے ایک مقالہ لکھا جس کا عنوان تھا واقعات کے امکانات کے ذریعہ واقعات کی وجوہات کے بارے میں ، جو الٹا امکانات کے مسائل کے بارے میں ہے۔ پہلے صفحے پر ، آپ بنیادی اصول پڑھ سکتے ہیں:

اگر کوئی واقعہ n مختلف وجوہات کی وجہ سے ہوسکتا ہے تو ، پھر ان وجوہات کے مابین تناسب واقعے کو دیئے گئے امکانات ان وجوہات کو دیئے گئے واقعات کے امکانات کے برابر ہیں۔ اور ہر وجہکے وجود کا امکان اس واقعے کو دیئے گئے وجوہات کے امکان کے برابر ہے جس میں ان وجوہات میں سے ہر ایک کو دیئے گئے واقعات کے کل امکانات سے تقسیم کیا گیا ہے۔

یہ وہی ہے جو آج ہم بایز تھیوریم کے طور پر جانتے ہیں:

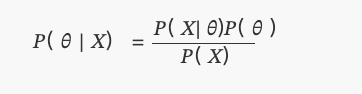
کہاںP(θ)ایک یکساں تقسیم ہے.

سکوں کا تجربہ

ہم بائیسن کے اعدادوشمار کو پیتھون اور پی آئی ایم سی لائبریری کا استعمال کرتے ہوئے موجودہ وقت میں لائیں گے، اور ایک سادہ تجربہ کریں گے.

فرض کریں کہ ایک دوست آپ کو ایک سکہ دیتا ہے اور پوچھتا ہے کہ کیا آپ کو لگتا ہے کہ یہ ایک منصفانہ سکہ ہے۔ کیونکہ اس کی جلدی ہے ، وہ آپ کو بتاتا ہے کہ آپ اس سکہ کو صرف 10 بار پھینک سکتے ہیں۔ جیسا کہ آپ دیکھ سکتے ہیں ، ایک نامعلوم پیرامیٹر ہےpاس مسئلے میں، جو کہ سکے پھینکنے میں سر حاصل کرنے کا امکان ہے، اور ہم سب سے زیادہ ممکنہ قدر کا اندازہ لگانا چاہتے ہیںp.

(نوٹ: ہم اس پیرامیٹر نہیں کہہ رہے ہیںpایک بے ترتیب متغیر ہے لیکن اس کے بجائے اس پیرامیٹر کو مقرر کیا جاتا ہے؛ ہم یہ جاننا چاہتے ہیں کہ یہ سب سے زیادہ امکان ہے.)

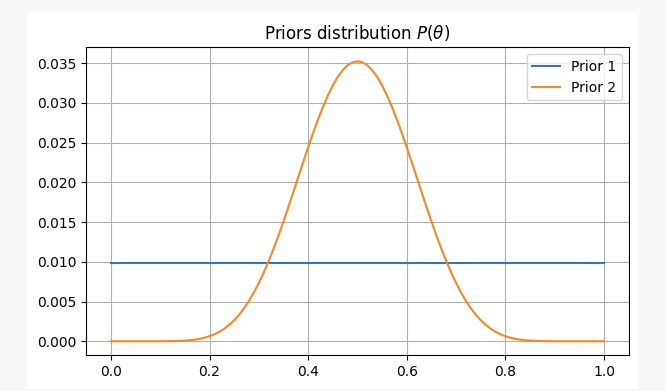
اس مسئلے کے بارے میں مختلف نظریات رکھنے کے لئے، ہم اسے دو مختلف سابقہ عقائد کے تحت حل کریں گے:

• 1. آپ کو سکہ کی انصاف کے بارے میں کوئی پیشگی معلومات نہیں ہے، لہذا آپ کو ایک برابر امکان تفویضpاس صورت میں، ہم استعمال کریں گے جو کہ غیر معلوماتی پہلے کہا جاتا ہے کیونکہ آپ نے اپنے عقائد میں کوئی معلومات شامل نہیں کی ہیں۔
• 2. آپ اپنے تجربے سے جانتے ہیں کہ اگرچہ ایک سکہ غیر منصفانہ ہو سکتا ہے، اسے انتہائی غیر منصفانہ بنانا مشکل ہے۔ لہذا آپ کو پیرامیٹر پر یقین ہےp0.3 سے کم یا 0.7 سے زیادہ ہونے کا امکان نہیں ہے۔ اس معاملے میں ، ہم ایک معلوماتی پہلے کا استعمال کریں گے۔

ان دونوں منظرناموں کے لئے، ہمارے پہلے عقائد مندرجہ ذیل ہوں گے:

ایک سکے کو 10 بار پھینکنے کے بعد، آپ کو دو بار سر ملے گا۔ اس ثبوت کے ساتھ، ہم اپنے پیرامیٹر کو کہاں تلاش کرنے کا امکان رکھتے ہیںp?

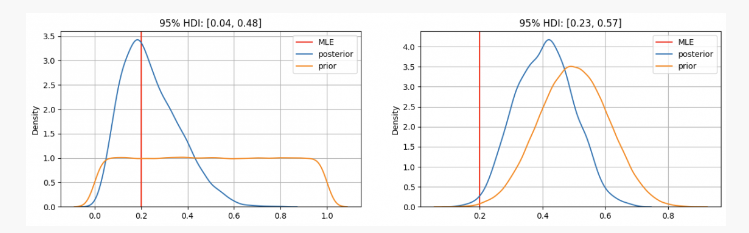
جیسا کہ آپ دیکھ سکتے ہیں، پہلی صورت میں، ہمارے پیرامیٹر کی پہلے تقسیمpزیادہ سے زیادہ امکان تخمینہ (ایم ایل ای) پر مرکوز ہےp=0.2، جو تعدد اسکول کے ذریعہ استعمال ہونے والے طریقہ کار کی طرح ہے۔ حقیقی نامعلوم پیرامیٹر 95٪ اعتماد کے وقفے کے اندر ہوگا ، 0.04 اور 0.48 کے درمیان۔

دوسری طرف، ایسے معاملات میں جہاں اعلی اعتماد ہے کہ پیرامیٹرp0.3 اور 0.7 کے درمیان ہونا چاہئے، ہم دیکھ سکتے ہیں کہ پیچھے کی تقسیم 0.4 کے ارد گرد ہے، جو ہمارے ایم ایل ای ہمیں دیتا ہے اس سے کہیں زیادہ ہے۔ اس صورت میں حقیقی نامعلوم پیرامیٹر 0.23 اور 0.57 کے درمیان 95٪ اعتماد کے وقفے کے اندر ہوگا۔

لہذا، پہلی صورت میں آپ اپنے دوست کو یقین کے ساتھ بتائیں گے کہ یہ سکہ منصفانہ نہیں ہے لیکن دوسری صورت میں آپ یہ کہیں گے کہ یہ غیر یقینی ہے کہ یہ منصفانہ ہے یا نہیں۔

جیسا کہ آپ دیکھ سکتے ہیں یہاں تک کہ جب ایک جیسے شواہد (دس میں سے دو سر پھینکنے) کا سامنا کرنا پڑتا ہے تو ، مختلف سابقہ عقائد کے تحت نتائج بہت مختلف ہوسکتے ہیں۔ روایتی طریقوں کے مقابلے میں بایسن کے اعدادوشمار کا ایک فائدہ یہ ہے: سائنسی طریقہ کار کی طرح یہ ہمیں نئے مشاہدات اور شواہد کے ساتھ ان کو جوڑ کر اپنے عقائد کو اپ ڈیٹ کرنے کی اجازت دیتا ہے۔

اختتام

آج کے مضمون میں ، ہم نے بایسن کے اعدادوشمار کی ابتدا اور اس کے اہم معاونین کو دیکھا۔ بعد میں اعدادوشمار کے اس شعبے میں بہت سے دوسرے اہم معاونین (جیفریز ، کوکس ، شینن وغیرہ) آئے ہیں ، جوquantdare.com.