SVM ভেক্টর মেশিন দিয়ে বাজি ধরে (বাণিজ্য করে) কি গরিলাদের ছাড়িয়ে যেতে পারো?

আজকে, আমরা আমাদের সর্বোচ্চ চেষ্টা করব একটি অরিন্দকে পরাজিত করার জন্য, যাকে আর্থিক জগতের সবচেয়ে ভয়ঙ্কর প্রতিদ্বন্দ্বী বলে মনে করা হয়। আমরা চেষ্টা করব এই মুদ্রা ব্যবসায়ের জাতের পরের দিনের মুনাফা অনুমান করতে। আমি আপনাকে আশ্বাস দিচ্ছি যে, একটি র্যান্ডম বাজিতে জয়লাভ করা এবং ৫০% লাভের সম্ভাবনা থাকা সত্ত্বেও, এটি একটি কঠিন কাজ। আমরা একটি মেশিন লার্নিং অ্যালগরিদম ব্যবহার করব যা ভেক্টর শ্রেণিবিন্যাসকে সমর্থন করে। এসভিএম ভেক্টর মেশিনগুলি রেগ্রেশন এবং শ্রেণিবিন্যাস কাজগুলি সমাধান করার জন্য একটি অবিশ্বাস্যভাবে শক্তিশালী পদ্ধতি।

• SVM ভেক্টর মেশিন সমর্থন করে

এসভিএম ভেক্টর মেশিনটি এই ধারণার উপর ভিত্তি করে তৈরি করা হয়েছেঃ আমরা p-ভেক্টর স্পেসের জন্য সুপারপ্লেইন ব্যবহার করে শ্রেণিবদ্ধ করতে পারি। এসভিএম ভেক্টর মেশিন অ্যালগরিদম একটি সুপারপ্লেইন এবং একটি সনাক্তকরণ মার্জিন ব্যবহার করে শ্রেণিবদ্ধকরণের সিদ্ধান্তের সীমানা তৈরি করে, যেমনটি নীচের চিত্রটিতে দেখানো হয়েছে।

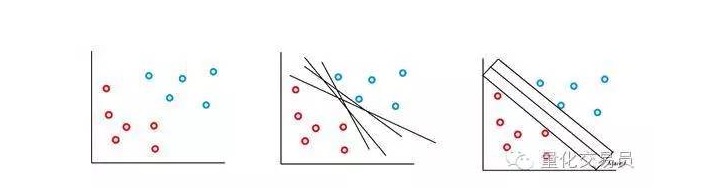
সবচেয়ে সহজ ক্ষেত্রে, রৈখিক শ্রেণীবিন্যাস সম্ভব। অ্যালগরিদম সিদ্ধান্তের সীমানা বেছে নেয়, যা শ্রেণীর মধ্যে দূরত্বকে সর্বাধিক করে তোলে।

বেশিরভাগ আর্থিক টাইম সিকোয়েন্সের ক্ষেত্রে, আপনি সহজ, লিনিয়ার বিভাজক সেটগুলির মুখোমুখি হতে পারবেন না, তবে অবিভাজক সেটগুলি প্রায়শই ঘটে থাকে। এসভিএম ভেক্টর মেশিনটি একটি পদ্ধতি প্রয়োগ করে এই সমস্যার সমাধান করে যা নরম মার্জিন পদ্ধতি হিসাবে পরিচিত।

এই ক্ষেত্রে, কিছু ভুল শ্রেণিবদ্ধকরণ অনুমোদিত, কিন্তু তারা নিজেরাই ফাংশনটি সম্পাদন করে, যাতে C (খরচ বা বাজেটের ত্রুটি অনুমোদিত হতে পারে) এর সাথে সমানুপাতিক ফ্যাক্টর এবং ত্রুটি থেকে সীমানা পর্যন্ত দূরত্বকে সর্বনিম্ন করা যায়।

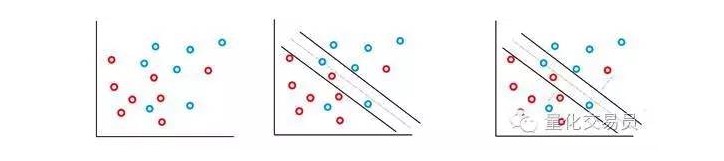
মূলত, মেশিনটি শ্রেণিবিন্যাসের মধ্যে যতটা সম্ভব ব্যবধানকে সর্বাধিক করে তোলে এবং তার C- ওজনের শাস্তি পয়েন্টগুলি যতটা সম্ভব কমিয়ে দেয়।

SVM শ্রেণিবিন্যাসকারী একটি চমৎকার বৈশিষ্ট্য আছে যে শ্রেণিবিন্যাস সিদ্ধান্তের সীমানার অবস্থান এবং আকার শুধুমাত্র সেই অংশের দ্বারা নির্ধারিত হয় যা সিদ্ধান্তের সীমানা থেকে নিকটতম। এই অ্যালগরিদমের বৈশিষ্ট্যটি এটিকে দূরবর্তী ব্যবধানের অস্বাভাবিক মানের হস্তক্ষেপের বিরুদ্ধে প্রতিরোধ করতে সক্ষম করে। যেমন উপরের চিত্রের নীল বিন্দু, সিদ্ধান্তের সীমানার উপর খুব কম প্রভাব ফেলে।

আমার মনে হয়, মজাটা তখনই শুরু হচ্ছে।

নিম্নলিখিত বিষয়গুলি বিবেচনা করুন (লাল বিন্দু এবং অন্যান্য রঙের বিন্দু আলাদা করুন):

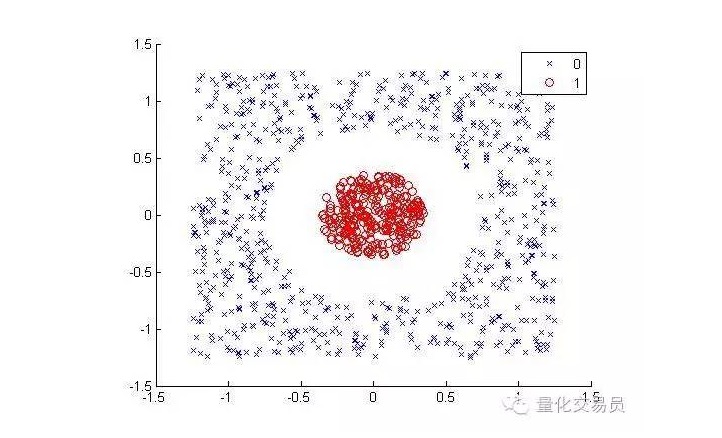
মানুষের জন্য, এটি খুব সহজেই শ্রেণিবদ্ধ করা যায় (একটি উপবৃত্তাকার লাইন) । কিন্তু মেশিনের জন্য এটি একই নয়। স্পষ্টতই, এটি একটি সরল রেখা তৈরি করতে পারে না (একটি সরল রেখা লাল বিন্দুগুলিকে আলাদা করতে পারে না) । এখানে আমরা কার্নেল কৌশল চেষ্টা করতে পারি (কার্নেল কৌশল) ।

ইন্দ্রকোষের কৌশল একটি অত্যন্ত বুদ্ধিমান গাণিতিক কৌশল যা আমাদেরকে উচ্চ মাত্রার (উচ্চায়িত) স্থানে রৈখিক শ্রেণিবিন্যাসের সমস্যা সমাধান করতে সক্ষম করে। এখন আসুন দেখি কিভাবে এটি করা হয়।

আমরা একটি 2D বৈশিষ্ট্য স্থানকে 3D তে রূপান্তর করব, এবং শ্রেণিবদ্ধকরণ শেষ হলে আমরা 2D তে ফিরে যাবো।

নীচে একটি মানচিত্রের মানচিত্র এবং শ্রেণিবদ্ধকরণ করা হয়েছেঃ

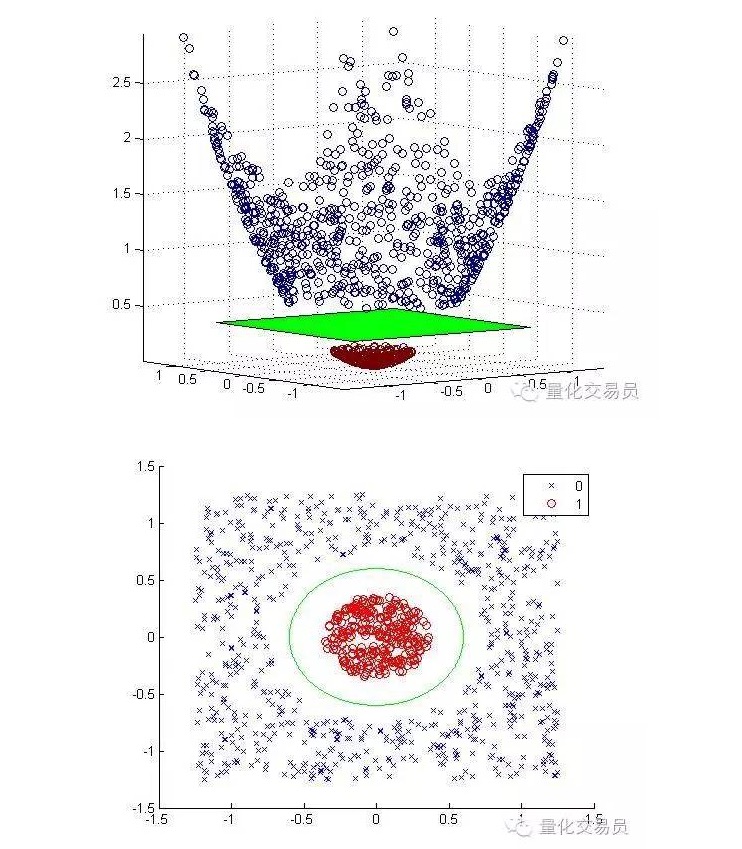
সাধারণভাবে, যদি d ইনপুট থাকে, তাহলে আপনি একটি মানচিত্র ব্যবহার করে d-dimensional ইনপুট স্পেস থেকে p-dimensional বৈশিষ্ট্য স্পেসে যেতে পারেন। উপরের সংক্ষিপ্তীকরণ অ্যালগরিদমের দ্বারা উত্পন্ন সমাধানগুলি চালান, এবং আপনার মূল ইনপুট স্পেসের p-dimensional সুপারফ্ল্যানটি ম্যাপ করুন।

উপরোক্ত গাণিতিক সমাধানের একটি গুরুত্বপূর্ণ পূর্বশর্ত, এটি নির্ভর করে কিভাবে একটি বৈশিষ্ট্যযুক্ত স্পেসে একটি ভাল বিন্দু নমুনা সেট তৈরি করা যায়।

আপনি শুধুমাত্র এই পয়েন্ট নমুনা সেট প্রয়োজন সীমানা অপ্টিমাইজেশান সঞ্চালন করতে, ম্যাপিং স্পষ্টতা প্রয়োজন হয় না, এবং ইনপুট স্থান উচ্চ মাত্রিক বৈশিষ্ট্যযুক্ত স্থান পয়েন্ট নিরাপদভাবে পারমাণবিক ফাংশন দ্বারা গণনা করা যেতে পারে (এবং Mercer এর উপপাদ্য সাহায্যে) ।

উদাহরণস্বরূপ, আপনি যদি আপনার শ্রেণিবদ্ধকরণ সমস্যাটি একটি বিশাল বৈশিষ্ট্য স্পেসে সমাধান করতে চান, ধরুন এটি 100,000 ডিগ্রি। আপনি কি কল্পনা করতে পারেন যে আপনার প্রয়োজনীয় গণনা ক্ষমতা কি? আমি আপনাকে এটি করতে সক্ষম হবে কিনা তা নিয়ে আমার খুব সন্দেহ আছে। ভাল, কার্নেল এখন আপনাকে এই বিন্দু নমুনা গণনা করতে দেয়, সুতরাং, এই প্রান্তটি আপনার কম ঘনত্বের আরামদায়ক ইনপুট স্পেস থেকে আসে।

• চ্যালেঞ্জ এবং গরিলা

এখন আমরা জেফের ভবিষ্যদ্বাণী করার ক্ষমতাকে পরাস্ত করার জন্য প্রস্তুত আছি।

জেফ অর্থ বাজারের একজন বিশেষজ্ঞ, যিনি র্যান্ডম বাজি দ্বারা 50% পূর্বাভাস নির্ভুলতা অর্জন করতে পারেন, যা পরবর্তী ট্রেডিং দিনের রিটার্নের পূর্বাভাসের সংকেত।

আমরা বিভিন্ন মৌলিক টাইম সিকোয়েন্স ব্যবহার করব, যার মধ্যে রয়েছে অফ-শপ মূল্যের টাইম সিকোয়েন্স, প্রতিটি টাইম সিকোয়েন্সের জন্য সর্বোচ্চ ১০ ল্যাগের আয়, মোট ৫৫ টি ফিচার।

আমরা যে এসভিএম ভেক্টর মেশিনটি তৈরি করতে যাচ্ছি তা হ’ল 3 ডিগ্রি কোর ব্যবহার করে। আপনি ভাবতে পারেন যে একটি উপযুক্ত কোর নির্বাচন করা আরেকটি খুব কঠিন কাজ, C এবং Γ প্যারামিটারগুলিকে ক্যালিব্রেট করার জন্য, সম্ভাব্য প্যারামিটারগুলির গ্রিডে 3 টি ক্রস যাচাইকরণ চালানো হবে এবং সেরা সেটটি নির্বাচিত হবে।

এর ফলে খুব একটা আশাব্যঞ্জক ফলাফল পাওয়া যায়নি:

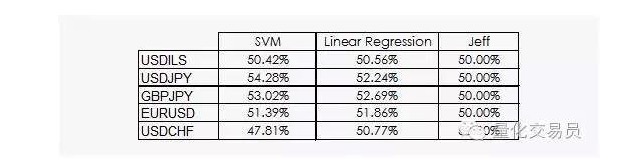
আমরা দেখতে পাচ্ছি যে, যে কোন লিনিয়ার রিগ্রেশন বা এসভিএম ভেক্টর মেশিন জেফকে পরাজিত করতে পারে। যদিও ফলাফলটি আশাবাদী নয়, আমরা তথ্য থেকে কিছু তথ্য বের করতে পারি, যা ইতিমধ্যে ভাল খবর, কারণ ডেটা বিভাগে, আর্থিক টাইম সিকোয়েন্সের দৈনিক উপার্জন সবচেয়ে কার্যকর নয়

ক্রস যাচাইয়ের পরে, ডেটাসেটটি প্রশিক্ষিত এবং পরীক্ষা করা হবে, আমরা প্রশিক্ষিত এসভিএমের পূর্বাভাসযোগ্যতা রেকর্ড করি, এবং একটি স্থিতিশীল পারফরম্যান্সের জন্য, আমরা প্রতিটি মুদ্রার জন্য 1000 টি র্যান্ডম বিভাজন পুনরাবৃত্তি করি।

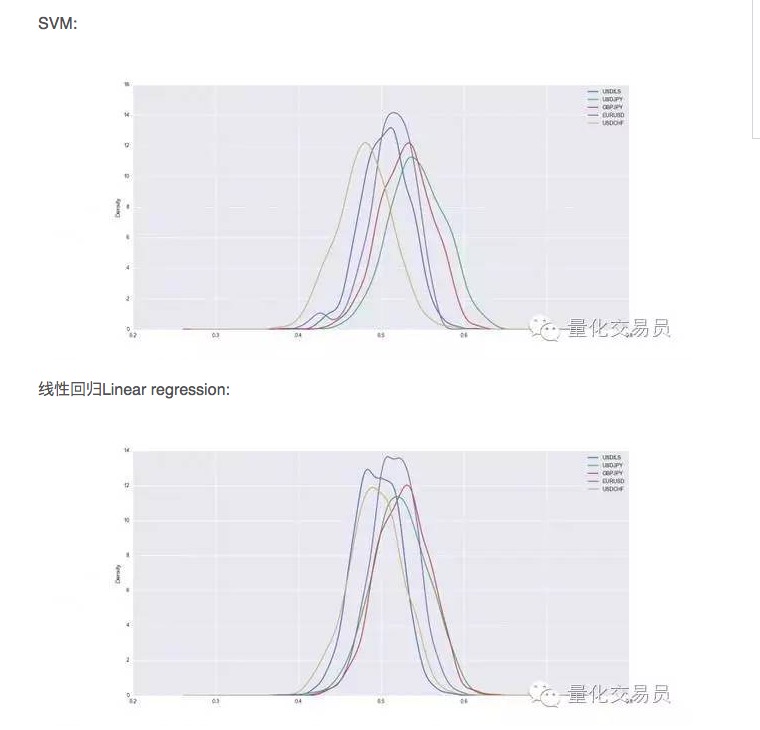
এইভাবে, কিছু ক্ষেত্রে, এসভিএম সহজ লিনিয়ার রিগ্রেশনের চেয়ে ভাল, তবে পারফরম্যান্সের পার্থক্যটি কিছুটা বেশি। উদাহরণস্বরূপ, ডলার-জেনের ক্ষেত্রে, আমরা যে সংকেতগুলি পূর্বাভাস দিতে পারি তার গড় পরিমাণ মোট সংখ্যার 54%। এটি একটি মোটামুটি ভাল ফলাফল, তবে আসুন আমরা আরও ঘনিষ্ঠভাবে দেখি!

টেড জেফের চাচাতো ভাই, এবং অবশ্যই এটিও একটি গরিলা, তবে এটি জেফের চেয়ে অনেক বেশি বুদ্ধিমান। টেড প্রশিক্ষণের নমুনা সেটগুলির দিকে নজর দেয়, এলোমেলোভাবে বাজি ধরার পরিবর্তে। তার বাজি সংকেতটি সর্বদা প্রশিক্ষণের সেটের সর্বাধিক সাধারণ আউটপুট থেকে দেওয়া হয়। আসুন এখন আমরা বুদ্ধিমান টেডকে একটি বেঞ্চমার্ক হিসাবে ব্যবহার করিঃ

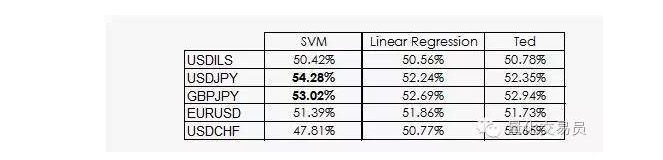
যেমনটি আমরা দেখেছি, বেশিরভাগ এসভিএমের পারফরম্যান্স কেবল একটি সত্য থেকে আসেঃ মেশিন লার্নিং যে শ্রেণিবদ্ধকরণটি প্রাইমারিটির সমান হওয়ার সম্ভাবনা নেই। প্রকৃতপক্ষে, লিনিয়ার রিগ্রেশন বৈশিষ্ট্য স্পেস থেকে কোনও তথ্য পেতে পারে না, তবে ছেদটি ((intercept) রেফারেন্সের ক্ষেত্রে অর্থবহ এবং ছেদটি একটি নির্দিষ্ট শ্রেণিবদ্ধকরণকে আরও ভালভাবে সম্পাদন করে।

আরেকটি ভাল খবর হলো, এসভিএম ভেক্টর মেশিন তথ্য থেকে কিছু অতিরিক্ত অ-রৈখিক তথ্য পেতে সক্ষম হয়েছে, যা আমাদের ভবিষ্যদ্বাণীকে ২% সঠিকতা দেয়।

দুর্ভাগ্যবশত, আমরা জানি না এটি কি ধরনের তথ্য হতে পারে, যেমন এসভিএম ভেক্টর মেশিনের নিজস্ব প্রধান অসুবিধাগুলি রয়েছে, যা আমরা ব্যাখ্যা করতে পারি না।

লেখকঃ পি লোপেজ, quantdare উইকিপিডিয়ার সর্বজনীন সংস্করণ থেকে পুনর্নির্দেশিত