মস্তিষ্কে ভেক্টর মেশিনগুলিকে সমর্থন করুন

সমর্থন ভেক্টর মেশিন (SVM) একটি গুরুত্বপূর্ণ মেশিন লার্নিং শ্রেণিবিন্যাসক, যা অ-রৈখিক রূপান্তর ব্যবহার করে একটি নিম্ন-মাত্রিক বৈশিষ্ট্যকে উচ্চ মাত্রায় প্রজেক্ট করে, যা আরও জটিল শ্রেণিবিন্যাসক কাজ সম্পাদন করতে পারে। SWM একটি গাণিতিক কৌতুক ব্যবহার করে, যা মস্তিষ্কের কোডিংয়ের সাথে সামঞ্জস্যপূর্ণ। আমরা 2013 সালের একটি প্রকৃতির নিবন্ধ থেকে পড়তে পারি এবং মেশিন লার্নিং এবং মস্তিষ্কের কাজ করার নীতিগুলির গভীর সংযোগ বুঝতে পারি। গবেষণার নামঃ জটিল জ্ঞানীয় কাজে মিশ্র নির্বাচনের গুরুত্ব (by Omri Barak al. )

• #### SVM

প্রথমত, আমরা নিউরাল কোডিংয়ের প্রকৃতি সম্পর্কে কথা বলিঃ একটি প্রাণী একটি নির্দিষ্ট সংকেত গ্রহণ করে এবং তার উপর ভিত্তি করে একটি নির্দিষ্ট আচরণ করে, একটি হল বাহ্যিক সংকেতকে নিউরো ইলেকট্রিক সংকেতে রূপান্তর করা, অন্যটি নিউরো ইলেকট্রিক সংকেতকে সিদ্ধান্ত নেওয়ার সংকেতে রূপান্তর করা, প্রথম প্রক্রিয়াটিকে এনকোডিং বলা হয়, এবং পরবর্তী প্রক্রিয়াটিকে ডিকোডিং বলা হয়। এবং নিউরাল কোডিংয়ের আসল উদ্দেশ্য হ’ল সিদ্ধান্ত নেওয়ার জন্য ডিকোডিং করা। সুতরাং, মেশিন লার্নিংয়ের সাথে চোখের কোডটি ডিকোড করার সবচেয়ে সহজ উপায় হ’ল একটি শ্রেণিবিন্যাসক, এমনকি একটি লজিস্টিক মডেলের একটি লিনিয়ার শ্রেণিবিন্যাসক, যা নির্দিষ্ট বৈশিষ্ট্য অনুসারে ইনপুট সংকেতকে শ্রেণিবিন্যাস করে। যেমন, একটি বাঘ পালিয়ে যাওয়া বা একটি বানরকে খাওয়া। অবশ্যই, কখনও কখনও কোডটি ভাল হয়, উদাহরণস্বরূপ, যখন একটি নিউরাল সংকেত অবশেষে গতিতে রূপান্তরিত হয়

এখন আসুন দেখি কিভাবে নিউরাল কোডিং করা হয়, প্রথমত নিউরনকে মূলত একটি আরসি সার্কিট হিসেবে দেখা যায়, যেটি প্রতিরোধক এবং ক্ষমতাকে বহির্মুখী ভোল্টেজ অনুযায়ী সামঞ্জস্য করে, এবং যখন বহির্মুখী সংকেত যথেষ্ট বড় হয়, তখন এটি প্রবাহিত হয়, অন্যথায় এটি বন্ধ হয়ে যায়, একটি নির্দিষ্ট সময়ের মধ্যে নির্গমনের ফ্রিকোয়েন্সি দ্বারা একটি সংকেতকে চিহ্নিত করে। এবং আমরা কোডিং সম্পর্কে কথা বলি, প্রায়শই সময়ের সাথে একটি বিচ্ছিন্ন প্রক্রিয়াকরণ করা হয়, একটি ছোট সময় উইন্ডোতে, এই নির্গমনের হারটি অপরিবর্তিত থাকে, তাই একটি নিউরাল নেটওয়ার্ক এই সময় উইন্ডোতে কোষের নির্গমনের হারকে একত্রিত করে একটি এন-ডাইমেনশনাল দিকনির্দেশ দেখতে পারে, N হল নিউরনের সংখ্যা, এই এন-ডাইমেনশনাল পরিমাণ, আমরা এটিকে কোডিং বলি, একটি চিত্র যা একটি প্রাণী দেখতে পারে, বা একটি শব্দ শুনতে পারে, যা সংশ্লিষ্ট স্তরগুলির নিউরাল নেটওয়ার্কের সংশ্লিষ্ট - অর্থাৎ বহির্মুখী

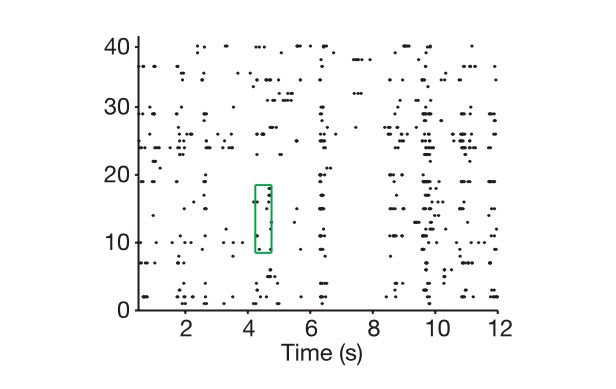
চিত্রঃ কোষের উপর, সময় দেখায় কিভাবে আমরা নিউরাল কোডিং বের করি।

N-dimensional vector আর neural coding এর মধ্যে পার্থক্য আছে, কিভাবে neural coding এর প্রকৃত মাত্রা নির্ধারণ করা যায়? প্রথমত, আমরা এই N-dimensional vector দ্বারা চিহ্নিত N-dimensional space এ প্রবেশ করি, তারপর আমরা সমস্ত সম্ভাব্য মিশ্রণ প্রদান করি, যেমন আপনাকে এক হাজার ছবি দেখাই, ধরে নিই যে এই ছবিগুলো সমগ্র বিশ্বকে প্রতিনিধিত্ব করে, এবং প্রতিবার আমরা যে Neural Coding পাই তা এই স্পেস এর একটি বিন্দু হিসেবে চিহ্নিত করি, এবং অবশেষে আমরা ভেক্টরীয় আলজেব্রিক চিন্তাধারার ব্যবহার করে এই হাজার বিন্দু দ্বারা গঠিত Subspace এর মাত্রা দেখি, অর্থাৎ Neural Signature এর প্রকৃত মাত্রা। আমি ধরে নিই যে এই N-dimensional space এর সকল বিন্দু আসলে এক লাইনের উপর অবস্থিত, তাহলে এই Signatureটি এক মাত্রিক হবে, যদি সব বিন্দুই একটি উচ্চ মাত্রিক plane এ থাকে, অর্থাৎ 2D space এর উপর।

কোডিং এর বাস্তব মাত্রা ছাড়াও, আমাদের একটি ধারণা আছে যে, বাহ্যিক সংকেতের বাস্তব মাত্রা, এখানে সংকেত হলো নিউরাল নেটওয়ার্ক দ্বারা প্রকাশিত বাহ্যিক সংকেত, অবশ্যই আপনাকে বাহ্যিক সংকেতের সব বিবরণ পুনরাবৃত্তি করতে হবে এটা একটা অসীম সমস্যা, কিন্তু আমাদের শ্রেণীবিন্যাস এবং সিদ্ধান্তের ভিত্তি সবসময়ই একটি গুরুত্বপূর্ণ বৈশিষ্ট্য, একটি মাত্রা হ্রাস প্রক্রিয়া, এটাও পিসিএ-র চিন্তা। এখানে আমরা বাস্তব কাজের মধ্যে একটি গুরুত্বপূর্ণ পরিবর্তনশীলকে কাজের বাস্তব মাত্রা হিসেবে বিবেচনা করতে পারি, যেমন ধরুন আপনি একটি হাতের গতি নিয়ন্ত্রণ করতে চাচ্ছেন, সাধারণত আপনাকে শুধু জয়েন্টের ঘূর্ণন কোণ নিয়ন্ত্রণ করতে হবে, যদি আপনি এটিকে একটি শক্ত বলবিজ্ঞানের সমস্যা হিসেবে দেখেন, তাহলে মাত্রা সম্ভবত ১০ এর বেশি হবে না, আমরা এটাকে কে বলি। এমনকি যদি এটি একটি মানুষের মুখের পার্থক্য করার মতো সমস্যা হয়, তাহলে মাত্রার সমস্যাটি এখনও অনেক কম।

তাই বিজ্ঞানীরা একটি মূল প্রশ্নের সম্মুখীন হচ্ছেন, কেন এই সমস্যা সমাধানের জন্য কোডিংয়ের মাত্রা এবং নিউরনের সংখ্যা ব্যবহার করা হচ্ছে যা প্রকৃত সমস্যার চেয়ে অনেক বেশি? এটা কি অপচয়?

এবং কম্পিউটিং নিউরোসায়েন্স এবং মেশিন লার্নিং একসাথে আমাদের বলে যে, নিউরোপ্রসেসিং এর উচ্চ মাত্রিক বৈশিষ্ট্যই এর উচ্চতর উচ্চশিক্ষার দক্ষতার ভিত্তি। কোডিংয়ের মাত্রা যত বেশি, শেখার ক্ষমতা তত বেশি। লক্ষ্য করুন যে আমরা এখানে গভীরতার নেটওয়ার্ক সম্পর্কেও কথা বলছি না। কেন? এখানে আমরা বলি যে স্নায়বিক কোডিংয়ের প্রক্রিয়াটি এসভিএম-এর মতো নীতি ব্যবহার করে, যখন আমরা একটি নিম্ন মাত্রিক সংকেতকে উচ্চ মাত্রায় প্রজেক্ট করি, আমরা যত বেশি শ্রেণিবিন্যাস করতে পারি, এমনকি যদি এটি একটি লিনিয়ার শ্রেণিবিন্যাসকারী হয় তবে আপনি অসংখ্য সমস্যার সমাধান করতে পারেন, এটি কীভাবে করা যায়? এটি কীভাবে এসভিএমের সাথে মেশিন নীতির সাথে সম্পর্কিত?

নোট করুন যে এখানে আলোচনা করা স্নায়ু কোডিং মূলত উচ্চতর স্নায়ু কেন্দ্রের স্নায়ু কোডিংকে বোঝায়, যেমন প্রিফ্রন্টাল কর্টেক্স (পিএফসি) যা এই নিবন্ধে আলোচনা করা হয়েছে, কারণ নিম্ন স্তরের স্নায়ু কেন্দ্রের কোডিং আইনগুলি শ্রেণিবদ্ধকরণ এবং সিদ্ধান্ত গ্রহণের সাথে খুব বেশি জড়িত নয়।

পিএফসি দ্বারা প্রতিনিধিত্ব করা উচ্চতর মস্তিষ্কের অঞ্চল

প্রথমত, আমরা ধরে নিই যে আমরা যখন আমাদের এনকোডিংয়ের মাত্রাটি একটি বাস্তব কাজের মধ্যে একটি গুরুত্বপূর্ণ পরিবর্তনশীল মাত্রার সমান হয় তখন আমরা একটি লিনিয়ার শ্রেণীবিভাগ ব্যবহার করে অ-রৈখিক শ্রেণীবিভাগের সমস্যার সাথে মোকাবিলা করতে সক্ষম হব না (যদি আপনি মটরশুটি থেকে একটি মটরশুটি আলাদা করতে চান তবে আপনি একটি লিনিয়ার বর্ডার দিয়ে মটরশুটিকে মটরশুটি থেকে আলাদা করতে পারবেন না) এবং এটি হ’ল একটি সাধারণ সমস্যা যা আমরা গভীর শিক্ষণ এবং এসভিএম-তে মেশিন লার্নিং না থাকলে সমাধান করতে পারি না। এই ধরণের সমস্যার জন্য এসভিএম-এর মূল ব্যাখ্যাটি পুনরায় চিত্রিত করা হয়, অর্থাৎ আমাদের মূল কোঅর্ডিনেটরি সিস্টেম থেকে একটি নতুন উচ্চতর কোঅর্ডিনেটরি সিস্টেমে রূপান্তর করা, যা বোঝায় যে আমরা যখন ক্লাসিকাল শ্রেণীবিভাগের পদ্ধতিটি ব্যবহার করতে পারি তখনও অ-রৈখিক শ্রেণীবিভাগ করতে পারি। (যদি আপনি মটরশুটি থেকে মটরশুটি আলাদা করতে চান তবে আপনি এটিকে একটি লিনিয়ার বর্ডার

SVM (ভেক্টর মেশিন সমর্থন):

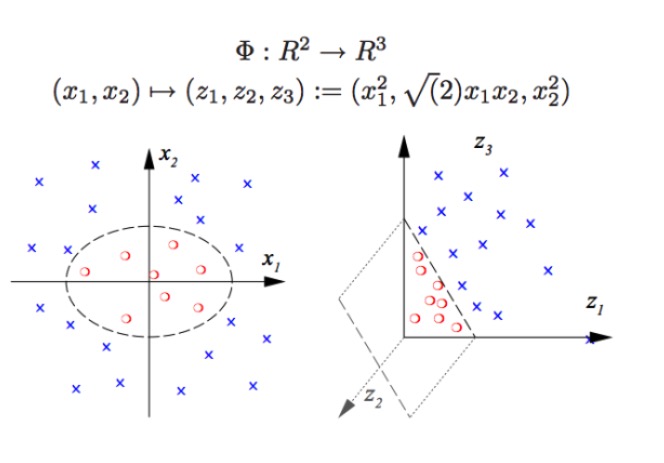
SVM অ-রৈখিক শ্রেণিবিন্যাস করতে পারে, উদাহরণস্বরূপ, চিত্রের লাল বিন্দু এবং নীল বিন্দু পৃথক করে, আমরা একটি রৈখিক সীমানা দিয়ে লাল বিন্দু এবং নীল বিন্দু পৃথক করতে পারি না (বাম চিত্র), তাই SVM ব্যবহারের পদ্ধতিটি মাত্রা বাড়ানো। এবং কেবলমাত্র পরিবর্তনশীল সংখ্যা যুক্ত করা কার্যকর নয়, যেমন (x1, x2) ম্যাপিং (x1, x2, x1 + x2) সিস্টেমটি আসলে দুই-মাত্রিক রৈখিক স্থান (একটি চিত্র আঁকতে হলে লাল বিন্দু এবং নীল বিন্দু একই সমতল) । কেবলমাত্র অ-রৈখিক ফাংশন (x1 ^ 2, x1) ব্যবহার করা হয়।*x2, x2^2) আমরা একটি মৌলিক নিম্ন মাত্রা থেকে উচ্চ মাত্রা অতিক্রম করেছি, এবং এই সময়ে আপনি নীল বিন্দুকে আকাশে ফেলে দেন, এবং তারপর আপনি আকাশে একটি সমতল আঁকুন, এবং নীল বিন্দুকে লাল বিন্দু থেকে আলাদা করুন, যেমন ডানদিকে দেখানো হয়েছে।

প্রকৃতপক্ষে, প্রকৃত নিউরাল নেটওয়ার্কগুলি ঠিক একই কাজ করে। এই ধরনের একটি লিনিয়ার ক্লাসিফায়ার (ক্রিপ্টার) দ্বারা পরিচালিত শ্রেণিবদ্ধকরণের প্রকারগুলি ব্যাপকভাবে বৃদ্ধি পেয়েছে, অর্থাৎ আমরা আগের তুলনায় অনেক বেশি শক্তিশালী প্যাটার্ন সনাক্তকরণ ক্ষমতা পেয়েছি। এখানে, উচ্চ মাত্রা উচ্চ শক্তি, উচ্চ মাত্রা আঘাত সত্য।

তাহলে কিভাবে নিউরাল কোডিং এর উচ্চ মাত্রা পাওয়া যায়? আলোক নিউরনের সংখ্যা বেশি হলে কোন লাভ নেই। কারণ আমরা লিনিয়ার অ্যালগরিদম শিখেছি যে, যদি আমাদের একটি বিশাল সংখ্যক N নিউরন থাকে এবং প্রতিটি নিউরনের স্রাবের হার শুধুমাত্র K কী বৈশিষ্ট্যের সাথে লিনিয়ারভাবে সম্পর্কিত হয়, তাহলে আমরা শেষ পর্যন্ত যে মাত্রাটি চিহ্নিত করি তা কেবলমাত্র সমস্যার মাত্রার সমান হবে, আপনার N নিউরনগুলি কোন কাজ করবে না ((অধিক সংখ্যক নিউরনগুলি K নিউরনের একটি লিনিয়ার সংমিশ্রণ) । এই বিন্দুটি অতিক্রম করার জন্য, আপনাকে K বৈশিষ্ট্যের অ-লিনিয়ারভাবে সম্পর্কিত নিউরন থাকতে হবে, এখানে আমরা অ-লিনিয়ার মিশ্রিত নিউরন বলে থাকি, এই ধরনের নিউরনগুলির উপস্থাপনা অত্যন্ত জটিল, এবং নীতিগতভাবে এসভিএম এর অ-লিনিয়ার কোডিং ফাংশনগুলির অনুরূপ। এই অ-লিনিয়ার নিউরনগুলির সাথে, একটি নিউরন কোডিংয়ের দক্ষতা বৈশিষ্ট্যযুক্ত মাত্রার কাজ করতে পারে।

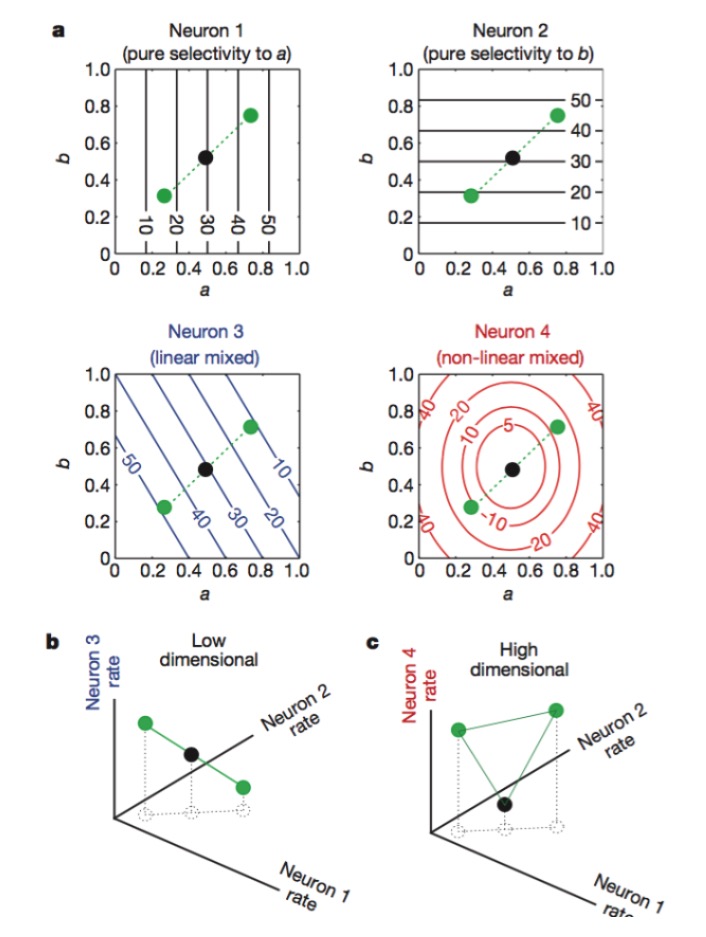
চিত্রঃ নিউরন ১ এবং ২ যথাক্রমে শুধুমাত্র বৈশিষ্ট্য a এবং b এর প্রতি সংবেদনশীল, ৩ বৈশিষ্ট্য a এবং b এর লিনিয়ার মিশ্রণের প্রতি সংবেদনশীল, এবং ৪ বৈশিষ্ট্যটির অ-লিনিয়ার মিশ্রণের প্রতি সংবেদনশীল। অবশেষে কেবল নিউরন ১, ২, ৪ এর সমন্বয়ই নিউরোন কোডিংয়ের মাত্রা বাড়িয়ে দেয় (নীচের চিত্র) ।

এই কোডিংয়ের অফিসিয়াল নাম হল মিশ্রিত কোডিং (mixed selectivity), যা আমরা তখন বুঝতে পারিনি যখন মানুষ এই কোডিংয়ের নীতিটি আবিষ্কার করেনি, কারণ এটি একটি নিউরাল নেটওয়ার্ক যা একটি নির্দিষ্ট ধরণের সংকেতের প্রতিক্রিয়া দেখায়। পার্শ্ববর্তী স্নায়ুতন্ত্রের মধ্যে, নিউরনগুলি সংকেতের বিভিন্ন বৈশিষ্ট্যগুলিকে এক্সট্র্যাক্ট এবং প্যাটার্ন সনাক্ত করার জন্য সেন্সরগুলির মতো কাজ করে। প্রতিটি নিউরন কোষের কার্যকারিতা বেশ নির্দিষ্ট, যেমন retina এর রডস এবং কনস ফোটন গ্রহণের জন্য দায়ী, এবং তারপরে গ্যাঞ্জেলিয়ন সেল কোডিং চালিয়ে যায়, প্রতিটি নিউরন একটি বিশেষভাবে প্রশিক্ষিত প্রহরী হিসাবে কাজ করে। এবং মস্তিষ্কের উচ্চতর অঞ্চলে, এই সুস্পষ্ট পার্থক্যটি দেখা যায় না, এবং আমরা দেখতে পাই যে একই নিউরন বিভিন্ন বৈশিষ্ট্যগুলির জন্য সংবেদনশীল হতে পারে, এবং এই সংবেদনশীলতাটি এখনও লিনিয়ার নয়। এটি বিভিন্ন ধরণের কাজগুলির জন্য একই ধরণের এবং একই রকমের মনে হয়), যা নিউরনগুলির জন্য এই ধরণের বিশেষ পদ্ধতিটি সনাক্ত করা কঠিন

প্রকৃতির প্রত্যেকটি বিবরণে ব্যানার রয়েছে, প্রচুর রিডার্বালিটি এবং মিশ্রিত কোডিং যা অ-পেশাদার বলে মনে হয়, যা একটি বিভ্রান্তিকর সংকেত বলে মনে হয়, যা শেষ পর্যন্ত আরও ভাল কম্পিউটিং ক্ষমতা দেয়। এই নীতির পরে, আমরা সহজেই কিছু কাজ করতে পারি যেমনঃ

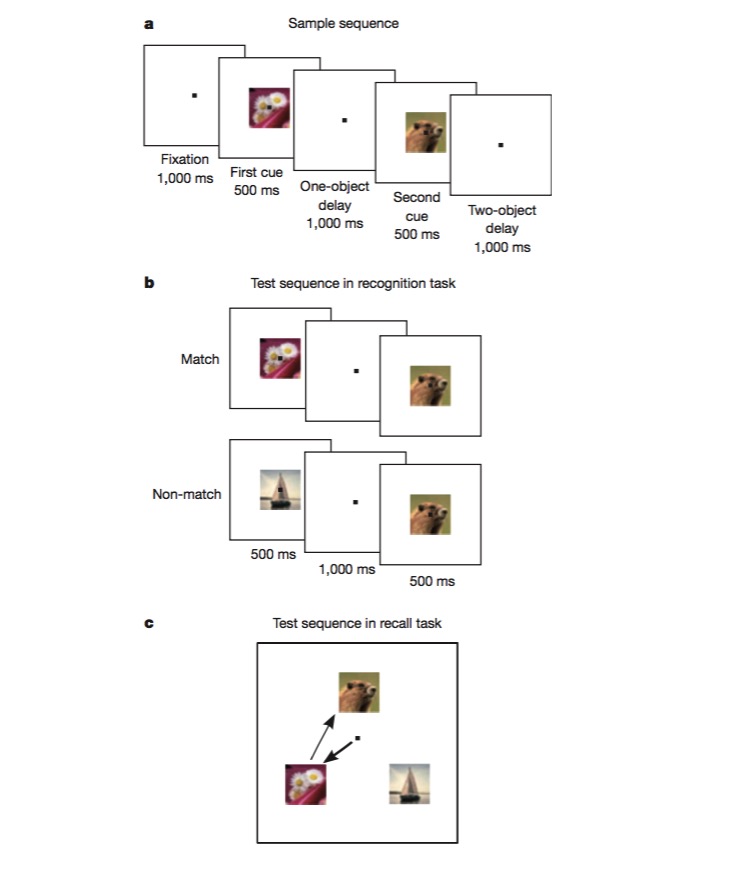
এই কাজটি করার জন্য, একটি বানরকে প্রথমে প্রশিক্ষণ দেওয়া হয় যে একটি চিত্রটি পূর্বের সাথে একই কিনা তা আলাদা করার জন্য এবং তারপরে দুটি ভিন্ন চিত্রের ক্রমানুসারে বিচার করার জন্য। এই কাজটি করার জন্য বানরকে বিভিন্ন দিকের কোডিং করতে সক্ষম হতে হবে, যেমন টাস্ক টাইপ, চিত্রের ধরণ ইত্যাদি, এবং এটিই একটি দুর্দান্ত পরীক্ষা যে কোনও মিশ্রিত নন-লাইনার কোডিং প্রক্রিয়া রয়েছে কিনা। পরীক্ষাগুলিতে প্রমাণিত হয়েছে যে প্রচুর সংখ্যক নিউরন মিশ্রিত বৈশিষ্ট্যের জন্য সংবেদনশীল এবং অ-লাইনার রয়েছে।

এই নিবন্ধটি পড়ে আমরা বুঝতে পেরেছি যে, স্নায়ুসংক্রান্ত নেটওয়ার্ক ডিজাইনের ক্ষেত্রে, কিছু অ-রৈখিক ইউনিট যুক্ত করলে প্যাটার্ন শনাক্তকরণের ক্ষমতা অনেকটাই বাড়বে, এবং এসভিএম ঠিক তাই করেছে, অ-রৈখিক শ্রেণিবিন্যাসের সমস্যা দূর করে দিয়েছে।

আমরা মস্তিষ্কের অংশগুলির কার্যকারিতা অধ্যয়ন করি, প্রথমে মেশিন লার্নিং পদ্ধতিতে ডেটা প্রক্রিয়া করি, যেমন পিসিএ দিয়ে সমস্যার মূল মাত্রা খুঁজে বের করা, তারপরে মেশিন লার্নিং প্যাটার্ন সনাক্তকরণের চিন্তাভাবনা দ্বারা নিউরাল কোডিং এবং কোডিং বোঝা, এবং শেষ পর্যন্ত আমরা যদি কিছু নতুন অনুপ্রেরণা পাই তবে আমরা মেশিন লার্নিংয়ের পদ্ধতিগুলি উন্নত করতে পারি। মস্তিষ্ক বা মেশিন লার্নিং অ্যালগরিদমের জন্য, শেষ পর্যন্ত সবচেয়ে গুরুত্বপূর্ণ বিষয় হ’ল তথ্যের সবচেয়ে উপযুক্ত উপস্থাপনা, এবং ভাল উপস্থাপনা সহ, সবকিছু সহজ। এটিই মেশিন লার্নিংয়ের ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে ধাপে

ছবিটি সৌজন্যে: