পূর্ববর্তী নিবন্ধটি দেখিয়েছিল কেন প্যারামিটারগুলি গতিশীলভাবে সামঞ্জস্য করা উচিত এবং কীভাবে অর্ডার আগমনের ব্যবধান অধ্যয়ন করে অনুমানের গুণমান মূল্যায়ন করা যায়। এই নিবন্ধটি গভীরভাবে তথ্যের উপর ফোকাস করবে এবং মধ্য-মূল্য (বা ন্যায্য-মূল্য, মাইক্রো-মূল্য ইত্যাদি) অধ্যয়ন করবে।

গভীরতার তথ্য

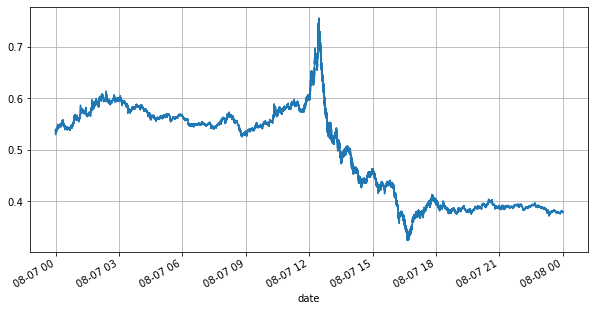
Binance সেরা উদ্ধৃতিগুলির ঐতিহাসিক ডেটা ডাউনলোড প্রদান করে, যার মধ্যে সেরা_বিড_মূল্য: সেরা বিড মূল্য, অর্থাৎ সর্বোচ্চ বিড মূল্য, সেরা_বিড_ক্যাটি: সেরা বিড মূল্যের পরিমাণ, সেরা_আস্ক_মূল্য: সেরা জিজ্ঞাসার মূল্য, সেরা_আস্ক_প্রমাণ: সেরার পরিমাণ মূল্য জিজ্ঞাসা করুন, লেনদেন_সময়: টাইমস্ট্যাম্প। এই ডেটা দ্বিতীয় স্তর এবং গভীর মুলতুবি আদেশ অন্তর্ভুক্ত করে না। এখানে বাজার বিশ্লেষণ করা হয়েছে 7 আগস্ট YGG। এই দিনে, বাজার খুব সহিংসভাবে ওঠানামা করেছিল, এবং ডেটার পরিমাণ 9 মিলিয়নেরও বেশি পৌঁছেছিল।

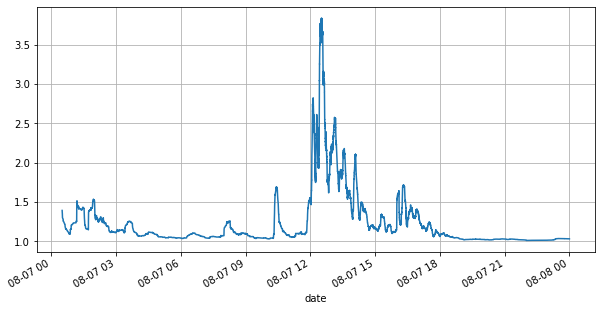
প্রথমত, দিনের বাজারের অবস্থার দিকে নজর দেওয়া যাক, এছাড়াও, দিনের অস্থির অর্ডারের সংখ্যাও ব্যাপকভাবে পরিবর্তিত হয়েছে (বিশেষ করে বিক্রয় মূল্য এবং ক্রয় মূল্যের মধ্যে পার্থক্য) খুব উল্লেখযোগ্যভাবে বাজারের প্রবণতা দেখায়। YGG-এর বাজারের পরিসংখ্যান অনুসারে, 20% সময় স্প্রেড 1 টিক বেশি হয় এই যুগে বিভিন্ন রোবট প্রতিদ্বন্দ্বিতা করে, এই পরিস্থিতি ইতিমধ্যেই বিরল।

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

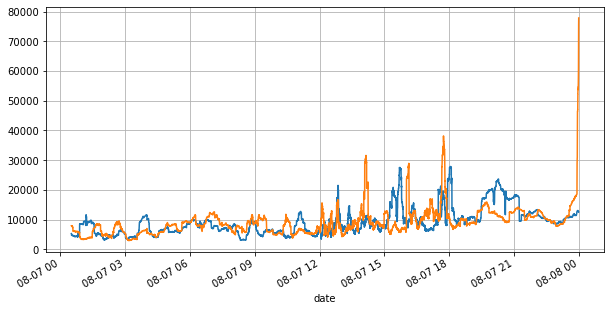
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

ভারসাম্যহীন উদ্ধৃতি

উপরোক্ত থেকে, আমরা দেখতে পাচ্ছি যে ক্রয় অর্ডার এবং বিক্রির অর্ডারের পরিমাণ বেশিরভাগ সময়ই খুব আলাদা হয় এই পার্থক্যটি স্বল্পমেয়াদী বাজারের অবস্থার উপর একটি শক্তিশালী ভবিষ্যদ্বাণীমূলক প্রভাব ফেলে। কারণটি আগের নিবন্ধে উল্লিখিত কারণের অনুরূপ যে ছোট কেনার অর্ডার পড়ে যাওয়ার প্রবণতা রয়েছে। যদি একদিকে মুলতুবি থাকা অর্ডারটি অন্য দিকের তুলনায় উল্লেখযোগ্যভাবে ছোট হয়, ধরে নিই যে সক্রিয় ক্রয়-বিক্রয় আদেশের পরিমাণ একই রকম, ছোট মুলতুবি থাকা অর্ডারটি খাওয়ার সম্ভাবনা বেশি হবে, যার ফলে মূল্য পরিবর্তনের প্রচার হবে। ভারসাম্যহীন উদ্ধৃতি I দ্বারা প্রতিনিধিত্ব করা হয়: 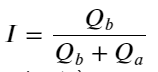তাদের মধ্যে, Q_b ক্রয় অর্ডারের পরিমাণ (best_bid_qty) প্রতিনিধিত্ব করে, এবং Q_a বিক্রয় অর্ডারের পরিমাণ (সর্বোত্তম_আস্ক_ক্যাটি) প্রতিনিধিত্ব করে।

সংজ্ঞা মধ্য-মূল্য: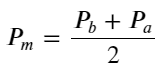

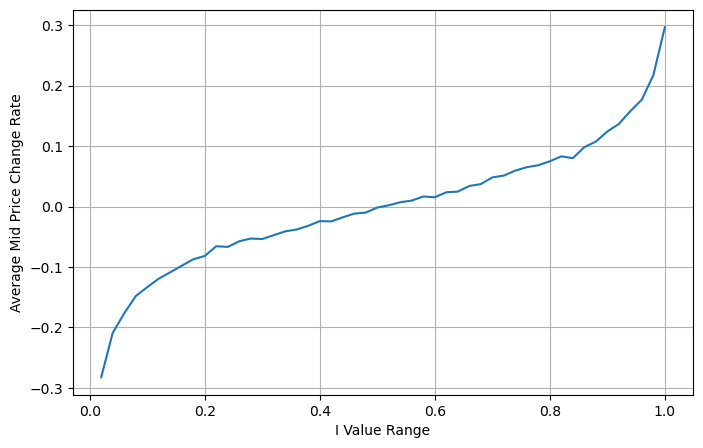
নীচের চিত্রটি পরবর্তী ব্যবধানে মধ্য-মূল্যের পরিবর্তনের হার এবং ভারসাম্যহীনতার মধ্যে সম্পর্ক দেখায়। এটি প্রত্যাশার সাথে সামঞ্জস্যপূর্ণ, আমি যত বাড়বে, মূল্য বৃদ্ধির সম্ভাবনা তত বেশি, এবং এটি 1-এর কাছাকাছি হবে। মূল্য পরিবর্তনের মাত্রাও ত্বরান্বিত হয়। উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং-এ, মধ্যম মূল্য প্রবর্তনের উদ্দেশ্য হল ভবিষ্যৎ মূল্যের পরিবর্তনগুলিকে আরও ভালভাবে অনুমান করা, অর্থাৎ, ভবিষ্যতের থেকে দামের পার্থক্য যত কম হবে, মধ্যমূল্যের সংজ্ঞা তত ভাল হবে। স্পষ্টতই মুলতুবি অর্ডারগুলির ভারসাম্যহীনতা কৌশলটির পূর্বাভাসের জন্য অতিরিক্ত তথ্য প্রদান করে, এটিকে বিবেচনায় রেখে, মধ্যম মূল্য নির্ধারণ করুন:

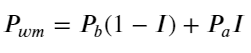
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

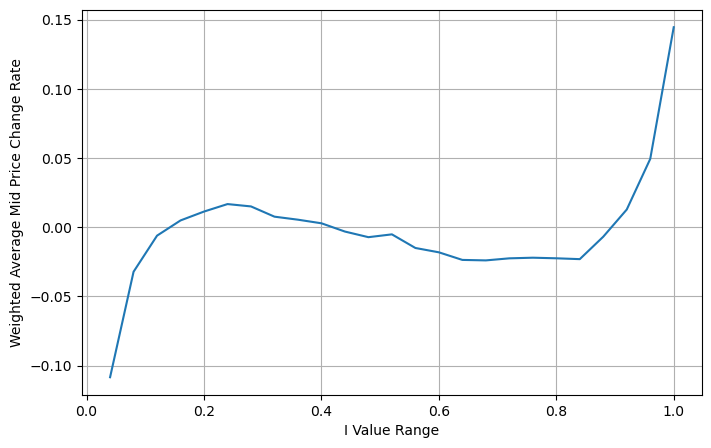
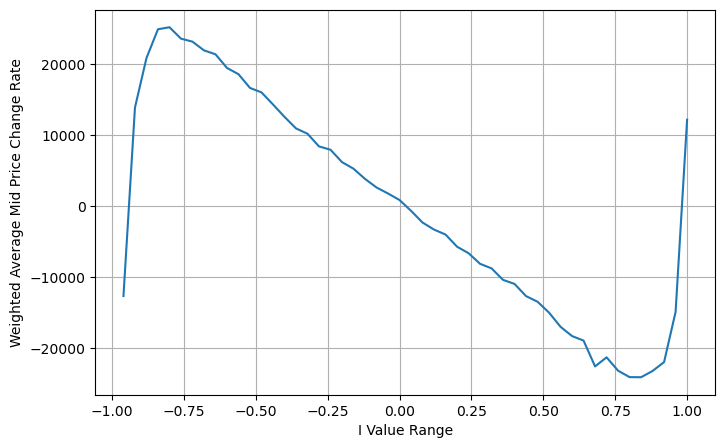
ওজন মাঝামাঝি দাম সামঞ্জস্য করুন

চিত্র থেকে, এটি দেখা যায় যে ভিন্ন I-এর তুলনায় ওজনযুক্ত মধ্য-মূল্যের পরিবর্তন অনেক ছোট, যা দেখায় যে ওজনযুক্ত মধ্য-মূল্যটি আরও উপযুক্ত। কিন্তু এখনও কিছু প্যাটার্ন আছে, যেমন প্রায় 0.2 এবং 0.8, বড় বিচ্যুতি সহ। এটি দেখায় যে আমি এখনও অতিরিক্ত তথ্য দিতে পারি। যেহেতু ওয়েটেড মিড-প্রাইস অনুমান করে যে দাম সংশোধন শব্দটি সম্পূর্ণরূপে রৈখিক, এটি স্পষ্টতই অবাস্তব, যেমনটি উপরের চিত্র থেকে দেখা যায়, যখন আমি 0 এবং 1 এর কাছাকাছি থাকি, তখন বিচ্যুতির গতি দ্রুততর হয় এবং তা নয়। একটি রৈখিক সম্পর্ক।

আরও স্বজ্ঞাতভাবে দেখার জন্য, এখানে “I” শব্দটি পুনরায় সংজ্ঞায়িত করা হয়েছে:

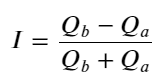
এই সময়ে:

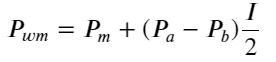
এই ফর্মটি পর্যবেক্ষণ করলে, আমরা দেখতে পাব যে ভারযুক্ত মধ্য-মূল্য হল গড় মধ্য-মূল্যের একটি সংশোধন, এবং সংশোধন শব্দটি হল I-এর একটি ফাংশন। ওজনযুক্ত মধ্য-মূল্য সহজভাবে অনুমান করে। এই সম্পর্ক হল I/2। এই সময়ে, I-এর সামঞ্জস্যপূর্ণ বন্টন (-1,1) এর সুবিধাগুলি I উৎপত্তি সম্পর্কে প্রতিসম, যা আমাদের জন্য ফাংশনের উপযুক্ত সম্পর্ক খুঁজে পেতে সুবিধা প্রদান করে। গ্রাফটি পর্যবেক্ষণ করলে, এই ফাংশনটি I-এর বিজোড় শক্তির সম্পর্ককে সন্তুষ্ট করবে, যা উভয় পক্ষের দ্রুত বৃদ্ধির সাথে সামঞ্জস্যপূর্ণ এবং উৎপত্তি সম্পর্কে প্রতিসম, এটি লক্ষ্য করা যায় যে উৎপত্তির কাছাকাছি মান রৈখিক উপরন্তু, যখন আমি 0, ফাংশন ফলাফল 0. যখন আমি 1, ফাংশন ফলাফল 0.5. তাই অনুমান এই ফাংশন মত দেখায়:

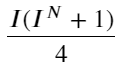
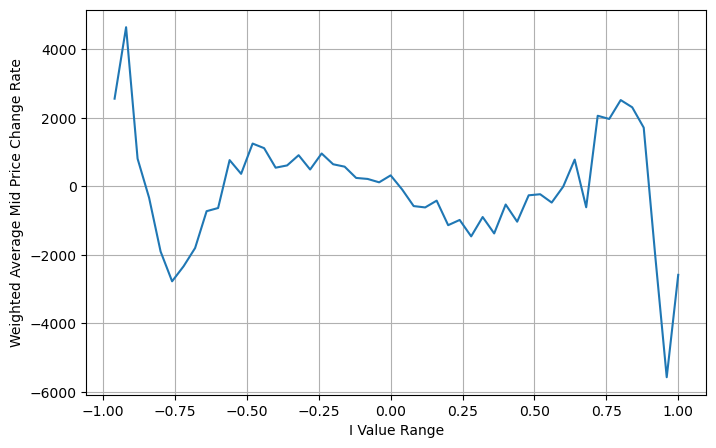
N এখানে একটি ধনাত্মক জোড় সংখ্যা প্রকৃত পরীক্ষার পরে, যখন N 8 হয় তখন এটি ভাল হয়। এখন পর্যন্ত এই নিবন্ধটি সংশোধিত ওজনযুক্ত মধ্যম মূল্যের প্রস্তাব করেছে:

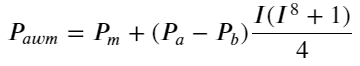
এই সময়ে, পূর্বাভাসিত কেন্দ্রীয় মূল্যের পরিবর্তনের সাথে মূলত আই-এর কোনো সম্পর্ক নেই। যদিও এই ফলাফলটি সাধারণ ওজনযুক্ত মধ্যমূল্যের চেয়ে ভাল, তবে এটি বাস্তব মূল্যের ক্ষেত্রে প্রয়োগ করা যাবে না। এস স্টোইকভের একটি 2017 নিবন্ধ মার্কভ চেইন পদ্ধতি চালু করেছেMicro-Price, এবং প্রাসঙ্গিক কোড দেওয়া আছে, আপনি এটি অধ্যয়ন করতে পারেন।

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

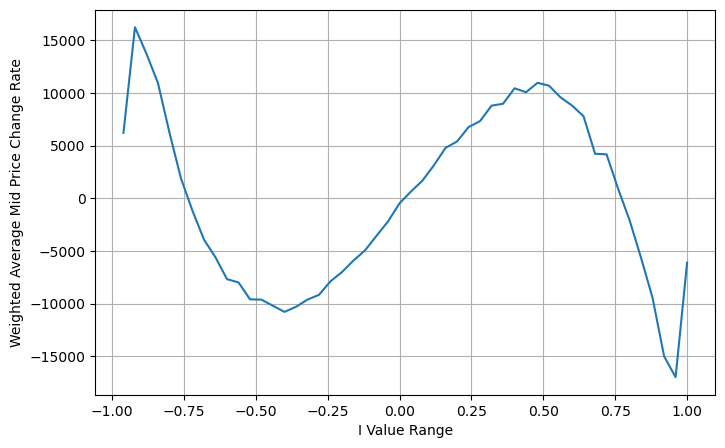
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

সারসংক্ষেপ

উচ্চ-ফ্রিকোয়েন্সি কৌশলগুলির জন্য মধ্যম মূল্য খুবই গুরুত্বপূর্ণ এটি ভবিষ্যতের স্বল্প-মেয়াদী মূল্যের পূর্বাভাস, তাই মধ্যম মূল্য যতটা সম্ভব সঠিক হতে হবে। পূর্বে প্রবর্তিত মধ্যম দামগুলি সবই প্রতিবন্ধী ডেটার উপর ভিত্তি করে, কারণ বিশ্লেষণে শুধুমাত্র একটি বাজার মূল্য ব্যবহার করা হয়। একটি বাস্তব অফারে, কৌশলটি যতটা সম্ভব সমস্ত ডেটা ব্যবহার করা উচিত, বিশেষ করে যদি প্রকৃত অফারে লেনদেন হয়, তবে মধ্যম মূল্যের পূর্বাভাস প্রকৃত লেনদেনের মূল্য দ্বারা পরীক্ষা করা উচিত। আমার মনে আছে স্টোইকভ একটি টুইট পোস্ট করেছেন, বলেছেন যে সত্যিকারের মধ্যমূল্যটি কেনা, বিক্রি এবং বন্ধ হওয়ার সম্ভাবনার ওজনযুক্ত গড় হওয়া উচিত এই সমস্যাটি পূর্ববর্তী নিবন্ধে অধ্যয়ন করা হয়েছিল। স্থান সীমাবদ্ধতার কারণে, এই বিষয়গুলি পরবর্তী নিবন্ধে বিস্তারিত আলোচনা করা হবে।