Im vorherigen Artikel wurde das Auftragsankunftsintervall untersucht und gezeigt, warum wir die Parameter dynamisch anpassen müssen und wie die Qualität der Schätzung bewertet wird. Dieser Artikel konzentriert sich auf detaillierte Daten und untersucht den Mittelpreis (auch fairer Preis, Mikropreis usw. genannt).

Tiefendaten

Binance bietet den Download historischer Daten der besten Kurse an, darunter best_bid_price: der beste Gebotspreis, d. h. der maximale Gebotspreis, best_bid_qty: die Nummer des besten Gebotspreises, best_ask_price: der beste Briefkurs, best_ask_qty: die Nummer des besten Briefkurses , transaction_time: Zeitstempel. Diese Daten umfassen nicht die zweite Ebene und tiefer liegende ausstehende Aufträge. Die hier analysierte Marktsituation ist die von YGG am 7. August. Die Marktschwankungen an diesem Tag waren sehr drastisch und die Datenmenge erreichte mehr als 9 Millionen.

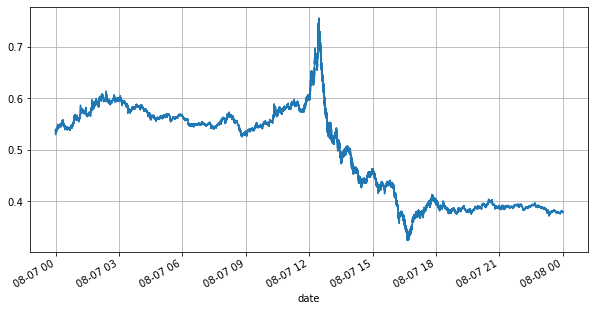
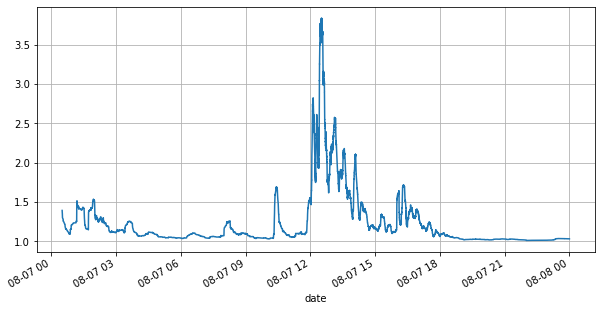
Schauen wir uns zunächst den Markt des Tages an. Er hat große Höhen und Tiefen. Darüber hinaus hat sich auch die Anzahl der anstehenden Aufträge am Tag mit den Schwankungen des Marktes stark verändert. Insbesondere der Spread (die Differenz zwischen dem Verkaufspreis und Kaufpreis) hat die Schwankungssituation des Marktes deutlich gezeigt. Laut den Marktstatistiken von YGG betrug der Spread an diesem Tag in 20 % der Fälle mehr als 1 Tick. In dieser Zeit, in der verschiedene Roboter auf dem Markt konkurrieren, ist diese Situation selten.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

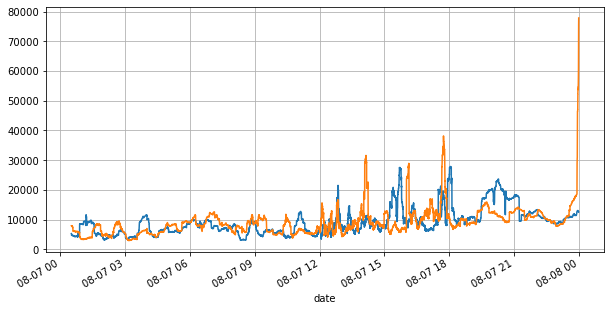
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

Unausgewogene Zitate

Aus dem Obigen können wir erkennen, dass die Volumina von Kauf- und Verkaufsaufträgen die meiste Zeit über sehr unterschiedlich sind. Dieser Unterschied hat einen starken prädiktiven Effekt auf die kurzfristigen Marktbedingungen. Der Grund hierfür ist ähnlich dem im vorherigen Artikel genannten Grund, nämlich dass kleine Kaufaufträge häufig zu Kursverlusten führen. Wenn die ausstehenden Aufträge auf der einen Seite deutlich kleiner sind als die auf der anderen Seite und vorausgesetzt, dass die Volumina der aktiven Kauf- und Verkaufsaufträge nahe beieinander liegen, ist es wahrscheinlicher, dass die Seite mit den kleineren ausstehenden Aufträgen aufgekauft wird, was den Preis in die Höhe treibt. Änderungen. Unausgeglichene Kurse werden durch I dargestellt: 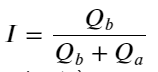Dabei stellt Q_b die Kaufauftragsmenge (best_bid_qty) und Q_a die Verkaufsauftragsmenge (best_ask_qty) dar.

Mittleren Preis definieren: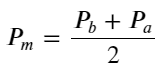

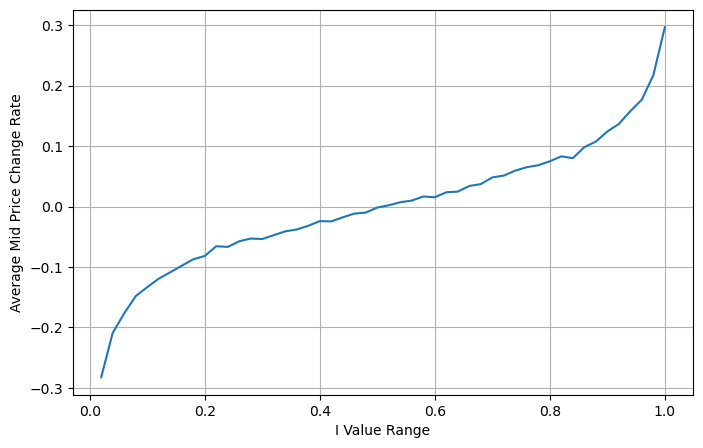
Die folgende Abbildung zeigt die Beziehung zwischen der Änderungsrate des Mittelpreises im nächsten Intervall und dem Ungleichgewicht I. Wie erwartet ist der Preisanstieg wahrscheinlicher, wenn I zunimmt, und je näher I bei 1 liegt, desto größer ist das Ausmaß des Auch die Preisänderungen beschleunigen sich. Beim Hochfrequenzhandel dient die Einführung des Mittelpreises dazu, zukünftige Preisänderungen besser vorhersagen zu können. Anders ausgedrückt: Je geringer die Differenz zum zukünftigen Preis ist, desto besser ist der Mittelpreis definiert. Offensichtlich liefert das Ungleichgewicht der ausstehenden Aufträge zusätzliche Informationen für die Prognose der Strategie. Unter Berücksichtigung dieser Tatsache definieren wir den gewichteten Mittelpreis:

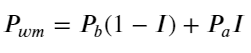
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

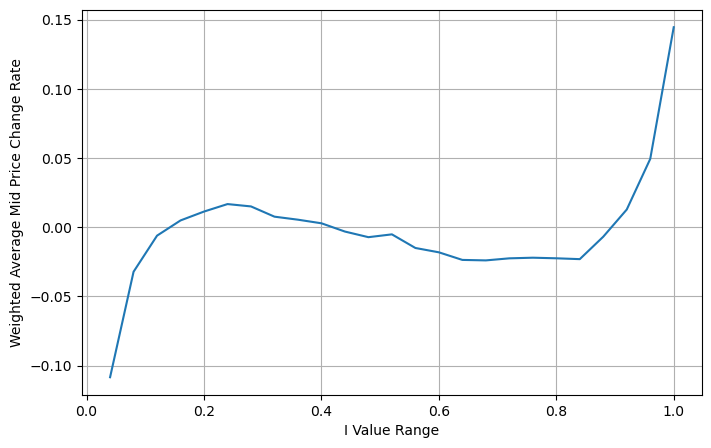
Anpassung des gewichteten Mittelpreises

Aus der Abbildung können wir erkennen, dass sich der gewichtete Mittelpreis viel weniger ändert als unterschiedliche I, was bedeutet, dass der gewichtete Mittelpreis besser passt. Es gibt aber dennoch einige Regelmäßigkeiten, etwa bei den Werten um 0,2 und 0,8, wo die Abweichungen relativ groß sind. Dies zeigt, dass ich noch zusätzliche Informationen beitragen kann. Da der gewichtete Mittelpreis davon ausgeht, dass der Preiskorrekturterm vollständig linear mit I ist, ist dies offensichtlich nicht wahr. Wie aus der obigen Abbildung ersichtlich ist, ist die Abweichung schneller, wenn I nahe bei 0 und 1 liegt, und es handelt sich nicht um eine lineare Beziehung.

Für ein intuitiveres Aussehen wird I hier neu definiert:

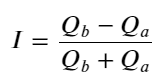
zu diesem Zeitpunkt:

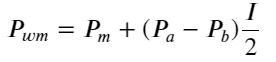
Wenn wir diese Form betrachten, können wir feststellen, dass der gewichtete Mittelpreis eine Korrektur des durchschnittlichen Mittelpreises ist. Der Koeffizient des Korrekturterms ist Spread, und der Korrekturterm ist eine Funktion von I. Der gewichtete Mittelpreis nimmt einfach an, dass diese Beziehung ist I/2. Zu diesem Zeitpunkt wird der Vorteil der angepassten Verteilung von I (-1,1) deutlich. I ist symmetrisch zum Ursprung, was es uns erleichtert, die Anpassungsbeziehung der Funktion zu finden. Betrachten Sie die Grafik. Diese Funktion sollte die Beziehung der ungeraden Potenz von I erfüllen, was mit dem schnellen Wachstum auf beiden Seiten und der Symmetrie um den Ursprung vereinbar ist. Darüber hinaus kann beobachtet werden, dass der Wert in der Nähe des Ursprungs nahezu linear ist. und wenn I 0 ist, ist das Funktionsergebnis 0, und wenn I 1 ist, ist das Funktionsergebnis 0,5. Schätzen Sie, diese Funktion sieht so aus:

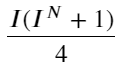
Hier ist N eine positive gerade Zahl. Nach tatsächlichen Tests ist es besser, wenn N 8 ist. Bisher schlägt dieser Artikel einen überarbeiteten gewichteten Mittelpreis vor:

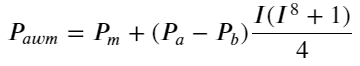
Zu diesem Zeitpunkt hat die Änderung des prognostizierten Mittelpreises im Grunde nichts mit I zu tun. Obwohl dieses Ergebnis besser ist als der einfache gewichtete Mittelpreis, kann es im tatsächlichen Handel nicht angewendet werden. Es ist hier nur eine Idee. Ein Artikel von S. Stoikov aus dem Jahr 2017 stellte die Markov-Ketten-Methode vorMicro-Price, und gibt den entsprechenden Code an, Sie können ihn auch studieren.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
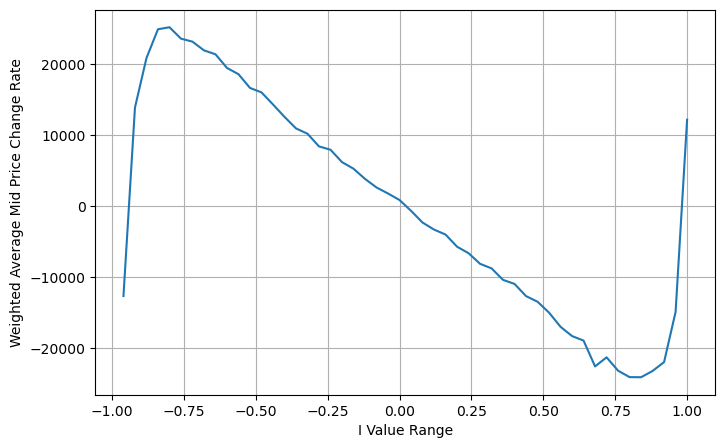
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

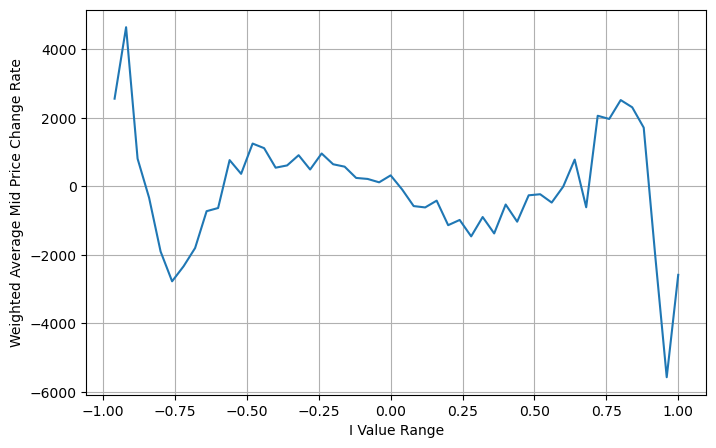
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

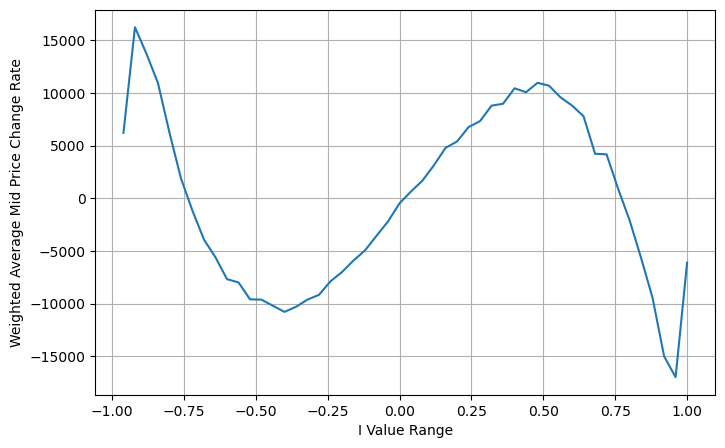
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Zusammenfassen

Der Mittelpreis ist für Hochfrequenzstrategien sehr wichtig. Er stellt eine Vorhersage zukünftiger kurzfristiger Preise dar und muss daher so genau wie möglich sein. Die oben eingeführten Mittelpreise basieren alle auf Marktdaten, da in der Analyse nur ein Marktpreis verwendet wird. Im realen Handel sollte die Strategie möglichst alle Daten nutzen, insbesondere wenn es im realen Handel zu Handelsbörsen kommt, und die Vorhersage des Mittelpreises sollte anhand des tatsächlichen Transaktionspreises getestet werden. Ich erinnere mich, dass Stoikov anscheinend einen Tweet gepostet hat, in dem er sagte, dass der reale Mittelpreis der gewichtete Durchschnitt der Wahrscheinlichkeit einer Buy-One-Sell-Transaktion sein sollte. Dieses Thema wurde gerade im vorherigen Artikel untersucht. Aus Platzgründen werden diese Probleme im nächsten Artikel ausführlich behandelt.