¿Es posible correr más rápido que los gorilas apostando (comerciando) con máquinas vectoriales SVM?

Señoras y señores, hagan sus apuestas. Hoy vamos a hacer todo lo posible para derrotar a un gorila, considerado uno de los rivales más temibles en el mundo financiero. Vamos a tratar de predecir el rendimiento del día a día de las variedades de las monedas que se negocian. Te aseguro que es muy difícil vencer a un gorila con una apuesta aleatoria y obtener un 50% de ganancia. Vamos a usar un algoritmo de aprendizaje automático que es compatible con el clasificador vectorial. La máquina vectorial SVM es una manera increíblemente poderosa para resolver tareas de regresión y clasificación.

• SVM soporta el vector

La máquina vectorial SVM está basada en la idea de que podemos clasificar el espacio de características de los pares p de un hiperplano. El algoritmo de la máquina vectorial SVM utiliza un hiperplano y un margen de identificación para crear la frontera de decisión de clasificación, como se muestra a continuación.

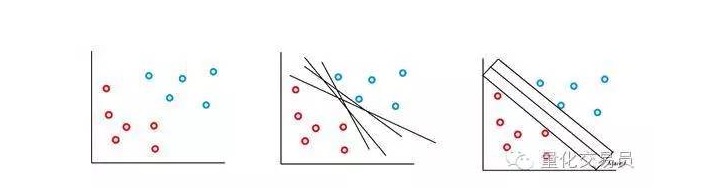
En el caso más simple, la clasificación lineal es posible. El algoritmo elige el límite de decisión, que puede maximizar la distancia entre las clases.

En la mayoría de las secuencias de tiempo financieras que se enfrentan, es poco probable que encuentren conjuntos separables simples y lineales, pero es frecuente que no lo sean. La máquina vectorial SVM resuelve este problema mediante la implementación de un método conocido como método de margen suave.

En este caso, se permiten algunas clasificaciones erróneas, pero ellas mismas ejecutan la función para reducir al mínimo el factor y la distancia del error a la frontera para que sea proporcional a C (errores de costo o presupuesto pueden ser permitidos).

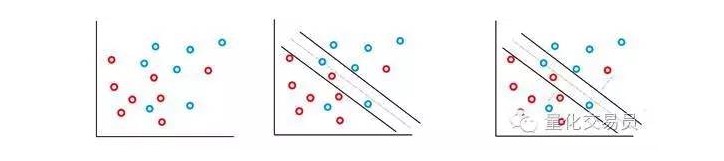
Básicamente, la máquina maximiza el espacio entre las clasificaciones y minimiza sus penalizaciones cargadas por C.

Una característica interesante del clasificador SVM es que la ubicación y el tamaño de los límites de la decisión de clasificación están determinados solo por parte de los datos, es decir, por la parte de los datos más cercana a los límites de la decisión. La característica de este algoritmo le permite resistir la interferencia de valores anormales a distancias muy lejanas.

¿No es demasiado complicado? Bueno, creo que la diversión está empezando.

Tenga en cuenta lo siguiente (separando los puntos rojos de los demás colores):

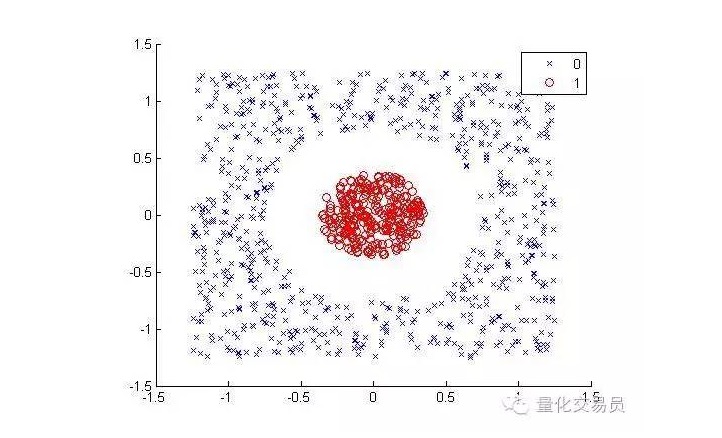
Para los humanos, la clasificación es muy sencilla (un hilo ovalado) pero no lo es para las máquinas. Obviamente, no se puede hacer una línea recta (una línea recta no puede separar los puntos rojos). Aquí podemos probar el truco del núcleo del núcleo.

La técnica del núcleo es una técnica matemática muy inteligente que nos permite resolver problemas de clasificación lineal en un espacio de dimensiones elevadas. Veamos cómo se hace.

Transformaremos el espacio de características bidimensionales en tridimensionales mediante el mapeo en escala, y volveremos a las dos dimensiones una vez terminada la clasificación.

A continuación se muestran los mapas en escala y los gráficos después de la clasificación:

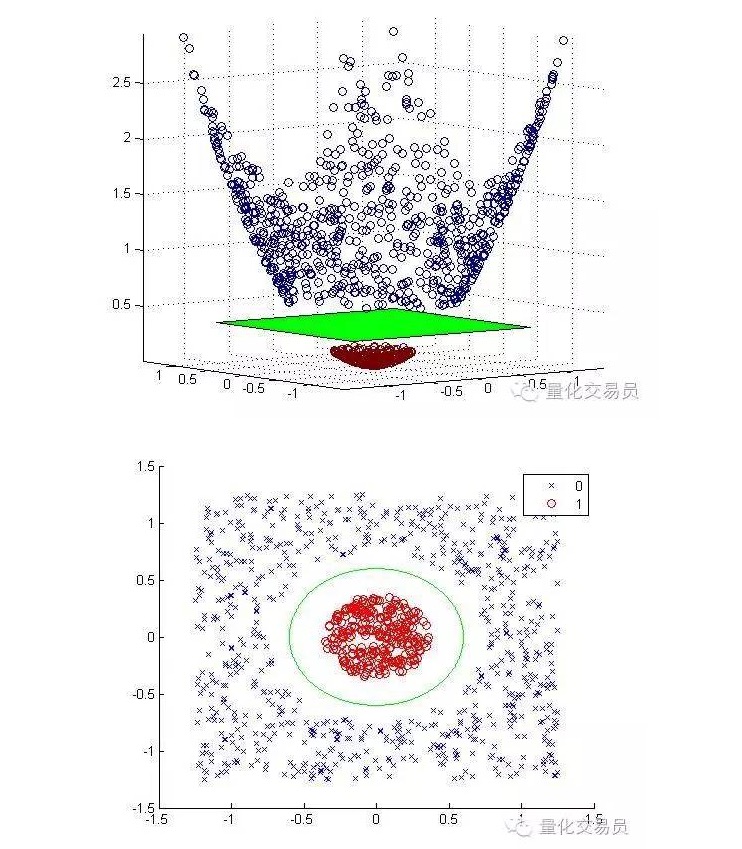
En general, si hay una entrada d, se puede usar un mapa desde el espacio de la entrada d-dimensional al espacio de la característica p-dimensional. Ejecutar la solución que el algoritmo de minimización anterior generará, y luego mapear el plano de la superposición p-dimensional de su espacio de entrada original.

La premisa importante de la solución matemática anterior depende de cómo generar un buen conjunto de muestras de puntos en el espacio de características.

Sólo necesitas un conjunto de muestras de estos puntos para realizar la optimización de la frontera, el mapeo no necesita ser definido, y los puntos del espacio de entrada en el espacio de características de alta dimensión pueden ser calculados de forma segura con la ayuda de la función nuclear (y un poco del teorema de Mercer).

Por ejemplo, si quieres resolver tu problema de clasificación en un espacio de características muy grande, supongamos que es de 100.000 dimensiones. ¿Te imaginas la capacidad de cálculo que necesitarías? Dudo mucho que puedas hacerlo.

• El desafío y los gorilas

Ahora estamos preparados para enfrentarnos al desafío de vencer a Jeff en la predicción.

Jeff es un experto en el mercado monetario, y puede obtener una precisión de predicción del 50% a través de apuestas aleatorias, una precisión que es una señal para predecir la rentabilidad del próximo día de negociación.

Usaremos diferentes secuencias de tiempo básicas, incluyendo la secuencia de tiempo de precios al contado, con ganancias de hasta 10 lags por cada secuencia de tiempo, para un total de 55 características.

La máquina vectorial SVM que estamos a punto de construir utiliza un núcleo de 3 grados. Como se puede imaginar, elegir un núcleo adecuado es otra tarea muy difícil, para calibrar los parámetros C y Γ, la triple cross-validation se ejecuta en una matriz de las combinaciones de parámetros posibles, y se seleccionará el mejor conjunto.

Los resultados no son muy alentadores:

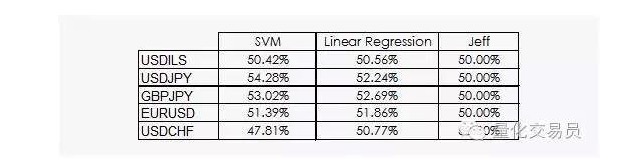
Podemos ver que tanto la regresión lineal como la máquina vectorial SVM pueden vencer a Jeff. Aunque los resultados no son optimistas, también podemos extraer información de los datos, lo cual ya es una buena noticia, ya que en la disciplina de datos, los beneficios diarios de la secuencia de tiempo financiera no son los más útiles.

Después de la verificación cruzada, el conjunto de datos será entrenado y probado, y registramos la capacidad de predicción de la SVM entrenada. Para tener un rendimiento estable, repetimos la división aleatoria de cada moneda 1000 veces.

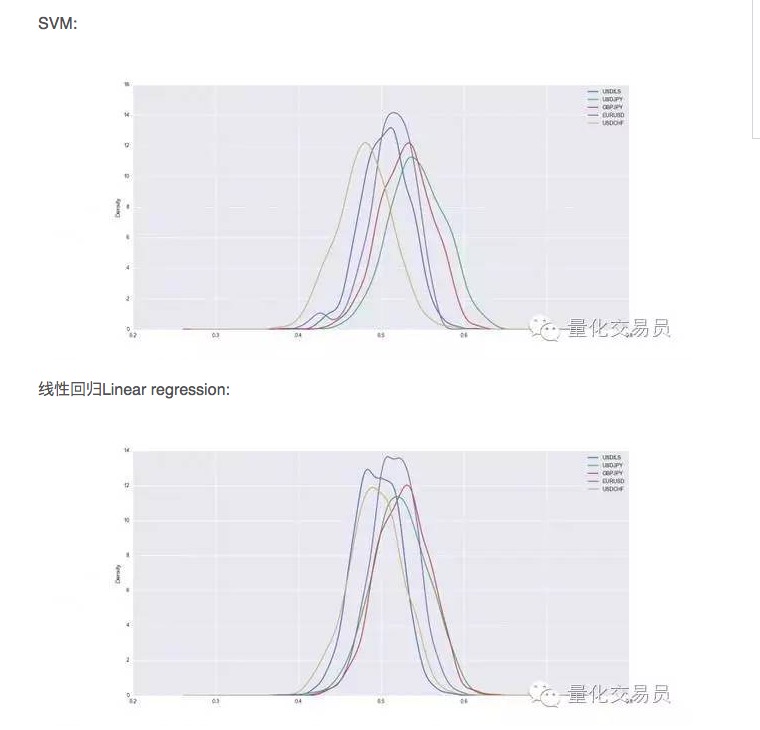
Así, en algunos casos, el SVM es mejor que la simple regresión lineal, pero la diferencia de rendimiento es un poco mayor. En el caso del dólar frente al yen, por ejemplo, el promedio de señales que podemos predecir representa el 54% del total. ¡Este es un resultado bastante bueno, pero veamos más de cerca!

Ted es el primo de Jeff, que por supuesto también es un gorila, pero es mucho más inteligente que Jeff. Ted mira el conjunto de muestras de entrenamiento, no las apuestas aleatorias.

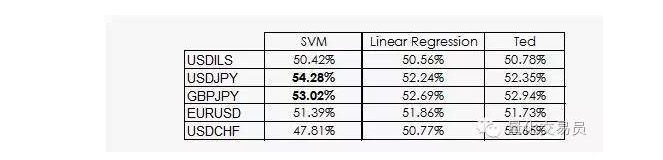
Como hemos visto, el rendimiento de la mayoría de las SVM solo proviene de un hecho: el aprendizaje de la máquina de que la clasificación es poco probable que sea equivalente a la prioridad. De hecho, la regresión lineal no puede obtener ninguna información del espacio de características, pero el intersector ((intercept) es significativo en la regresión, y el intersector y la columna de una clasificación se comportan mejor que la columna de este hecho.

Una noticia un poco mejor es que la máquina vectorial SVM puede obtener información no lineal adicional de los datos, lo que nos permite tener una precisión de predicción del 2%.

Desafortunadamente, no sabemos qué tipo de información puede ser, como si el vector SVM tuviera sus principales desventajas, que no podemos explicar claramente.

El autor: P. López, publicado en quantdare Se publicó en el sitio web de WeChat.