Reflexiones sobre estrategias de trading de alta frecuencia (1)
 3
3
 4856
4856

El artículo analiza las estrategias de negociación de alta frecuencia de las monedas digitales, incluidas las fuentes de ganancias (principalmente de las fluctuaciones del mercado y los descuentos en las tarifas de cambio), las cuestiones de colocación de órdenes y control de posiciones, y el método de modelado del volumen de negociación utilizando la distribución de Pareto. Además, los datos de transacciones y órdenes óptimas proporcionados por Binance se utilizaron para realizar pruebas retrospectivas, y está previsto discutir en profundidad otros temas de estrategias comerciales de alta frecuencia en artículos posteriores.
Ya he escrito dos artículos sobre el comercio de alta frecuencia de monedas digitales. Una introducción detallada a las estrategias de alta frecuencia para monedas digitales, Gana 80 veces en 5 días, el poder de la estrategia de alta frecuencia. Pero esto sólo puede considerarse como un intercambio de experiencias y una conversación general. Esta vez planeo escribir una serie de artículos para presentar las ideas del trading de alta frecuencia desde el principio. Espero ser lo más conciso y claro posible. Sin embargo, debido a mi limitado nivel y comprensión profunda del trading de alta frecuencia, Trading, este artículo es solo un punto de partida. Espero que los expertos puedan corregirme.
Fuentes de ganancias de alta frecuencia
Como se mencionó en artículos anteriores, las estrategias de alta frecuencia son particularmente adecuadas para mercados con altibajos extremadamente volátiles. Examinar los cambios de precios de un producto comercial en un corto período de tiempo, que consta de tendencias y fluctuaciones generales. Si podemos predecir con precisión los cambios en las tendencias, sin duda podremos ganar dinero, pero esto también es lo más difícil. Este artículo presenta principalmente estrategias de creación de alta frecuencia y no abordará este tema. En un mercado volátil, si la estrategia de colocar órdenes al alza y a la baja se ejecuta con suficiente frecuencia y el margen de beneficio es lo suficientemente grande, puede cubrir las posibles pérdidas causadas por la tendencia, de modo que puede obtener ganancias sin predecir el mercado. En la actualidad, todas las transacciones de los creadores en las bolsas reciben descuentos en las tarifas de transacción, lo que también es un componente de las ganancias. Cuanto más intensa sea la competencia, mayor debe ser la proporción de descuentos.
Problema a resolver
La estrategia coloca órdenes de compra y de venta al mismo tiempo. La primera pregunta es dónde colocar las órdenes. Cuanto más cerca esté la orden del mercado, mayor será la probabilidad de una transacción. Sin embargo, en un mercado volátil, el precio de transacción instantáneo puede estar muy alejado del mercado. Si la orden se coloca demasiado cerca, no podrá realizar una transacción. obtener suficientes ganancias La probabilidad de ejecución de órdenes colocadas demasiado lejos es baja. Este es un problema que necesita ser optimizado.
Controla tu posición. Para controlar los riesgos, la estrategia no puede acumular demasiadas posiciones durante mucho tiempo. Esto se puede solucionar controlando la distancia del pedido, la cantidad del pedido, el límite de posición total, etc.
Para lograr los objetivos anteriores, es necesario modelar y estimar la probabilidad de transacción, la ganancia de la transacción, la estimación del mercado y otros aspectos. Hay muchos artículos y documentos en esta área, que se pueden encontrar con palabras clave como Comercio de alta frecuencia , Cartera de pedidos, etc. Hay muchas recomendaciones en línea, en las que no entraré aquí. Además, lo mejor es establecer un sistema de backtesting rápido y fiable. Aunque las estrategias de alta frecuencia se pueden verificar fácilmente mediante operaciones reales para comprobar su eficacia, el backtesting puede aportar más ideas y reducir el coste del ensayo y error.
Datos requeridos
Binance proporciona datos de transacciones por transacción y de mejores órdenesdescargarLos datos profundos deben descargarse utilizando la API en la lista blanca, o puede recopilarlos usted mismo. Para fines de backtesting, puedes simplemente utilizar los datos de transacciones recopilados. Este artículo toma los datos de HOOKUSDT-aggTrades-2023-01-27 como ejemplo.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Las columnas de transacciones son las siguientes:
- agg_trade_id: el identificador de la orden de transacción agregada,
- Precio: precio de transacción
- Cantidad: El número de transacciones
- first_trade_id: Puede haber varias transacciones en la colección al mismo tiempo, solo se cuenta un dato, este es el id de la primera transacción
- last_trade_id: el id de la última transacción
- transact_time: tiempo de transacción
- is_buyer_maker: dirección de la transacción, Verdadero significa que la orden de compra la negocia el creador y la orden de venta la negocia el tomador
Se puede ver que ese día hubo 660.000 datos de transacciones y las transacciones fueron muy activas. El csv se adjuntará en la sección de comentarios.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
Modelado del volumen de transacciones individuales
Primero, procese los datos y divida las transacciones originales en el grupo de transacciones activas de órdenes de compra y el grupo de transacciones activas de órdenes de venta. Además, los datos de transacciones agregadas originales son un conjunto de datos al mismo tiempo, al mismo precio y en la misma dirección. Puede haber una orden de compra activa de 100. Si se divide en múltiples transacciones con diferentes precios, como Como 60 y 40, se generarán dos piezas de datos que afectarán la estimación del volumen de órdenes de compra. Por lo tanto, es necesario agregar nuevamente en función de transact_time. Después de la agregación, la cantidad de datos se redujo en 140.000 registros.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
Tomando como ejemplo las órdenes de compra, primero dibujemos un histograma. Se puede ver que el efecto de cola larga es muy obvio. La mayoría de los datos se concentran en el extremo izquierdo, pero también hay una pequeña cantidad de transacciones grandes distribuidas en la cola. .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
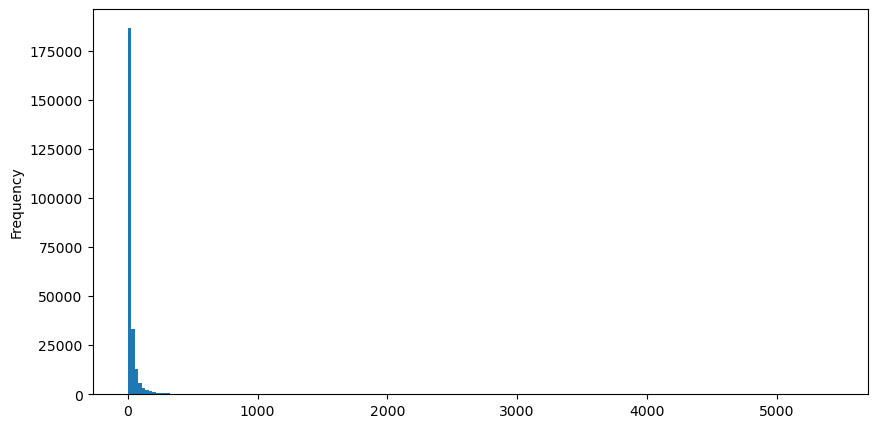
Para facilitar la observación, cortamos la cola y observamos. Podemos ver que cuanto mayor es el volumen de operaciones, menor es la frecuencia de ocurrencia y más rápida la tendencia de disminución.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
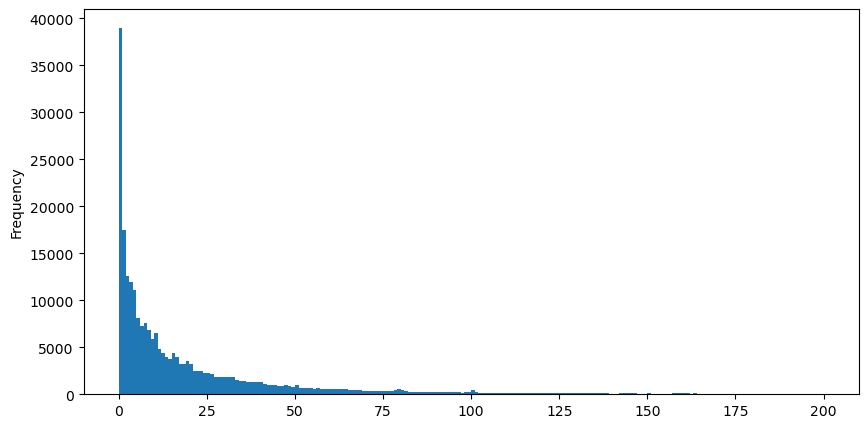
Hay muchos estudios sobre la distribución de la satisfacción con el volumen. Su distribución de ley de potencia también se llama distribución de Pareto, que es una forma común de distribución de probabilidad en física estadística y ciencias sociales. En una distribución de ley de potencia, la probabilidad de un evento de cierto tamaño (o frecuencia) es proporcional a algún exponente negativo del tamaño de ese evento. La característica principal de esta forma de distribución es que los eventos grandes (es decir, aquellos alejados de la media) ocurren con mayor frecuencia de lo que se esperaría en muchas otras distribuciones. Esta es la característica de la distribución del volumen comercial. La forma de la distribución de Pareto es: P(x) = Cx^(-α). Lo siguiente demostrará esto.
La siguiente figura muestra la probabilidad de que el volumen de operaciones sea mayor que un valor determinado. La línea azul es la probabilidad real y la línea naranja es la probabilidad simulada. No se preocupe por los parámetros específicos aquí. Puede ver que sí. satisfacer la distribución de Pareto. Dado que la probabilidad de que el volumen del pedido sea mayor que 0 es 1, y para cumplir con los requisitos de estandarización, la ecuación de distribución debe ser la siguiente:
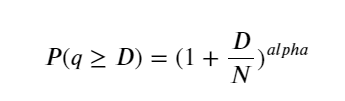
Donde N es el parámetro estandarizado. Aquí seleccionamos volumen promedio M y alfa -2,06. La estimación específica de alfa se puede calcular calculando inversamente el valor P cuando D=N. Específicamente: alfa = log(P(d>M))/log(2) . Elegir diferentes puntos dará como resultado valores alfa ligeramente diferentes.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
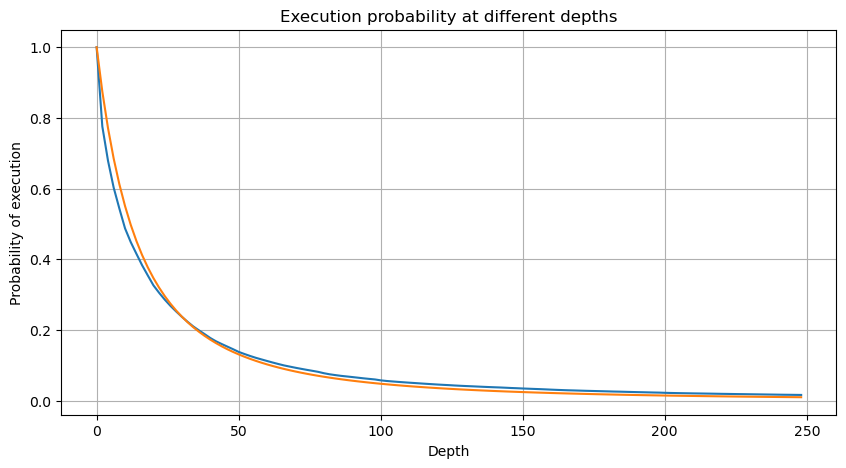
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
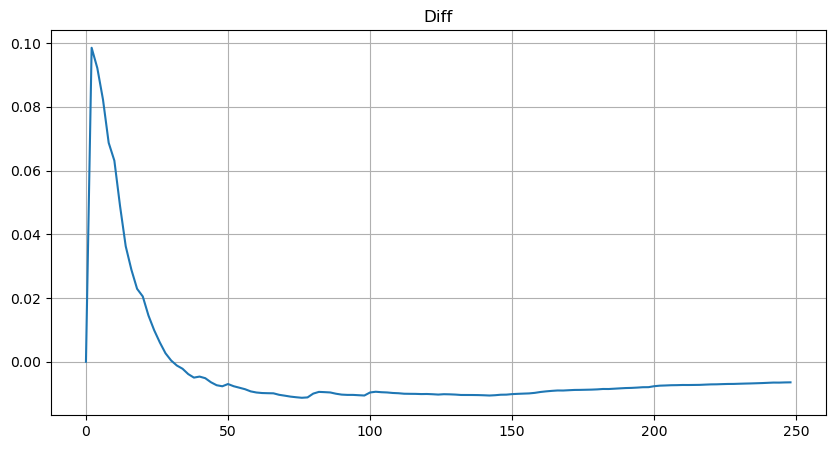
Pero esta estimación es solo una apariencia. En la figura anterior, graficamos la diferencia entre el valor simulado y el valor real. Cuando el volumen de negociación es pequeño, la desviación es grande, incluso cercana al 10%. La probabilidad de un punto se puede hacer más precisa seleccionando diferentes puntos durante la estimación de parámetros, pero esto no resuelve el problema de la desviación. Esto se determina por la diferencia entre la distribución de la ley de potencia y la distribución real. Para obtener resultados más precisos, es necesario corregir la ecuación de la distribución de la ley de potencia. No entraré en detalles sobre el proceso específico, pero tuve un destello de inspiración y descubrí que en realidad debería ser así:
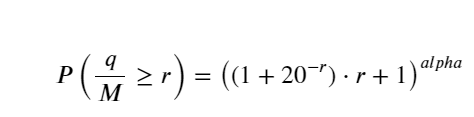
Para simplificar, aquí se utiliza r = q/M para representar el volumen comercial estandarizado. Los parámetros se pueden estimar de la misma manera que anteriormente. La siguiente figura muestra que la desviación máxima después de la corrección no supera el 2 %. En teoría, la corrección puede continuar, pero esta precisión es suficiente.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
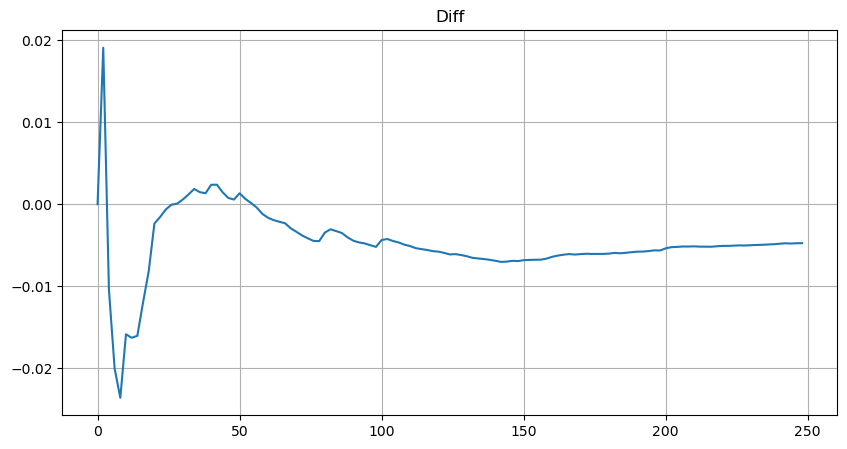
Con la ecuación estimada para la distribución del volumen, tenga en cuenta que la probabilidad de la ecuación no es la probabilidad real, sino una probabilidad condicional. En este punto podemos responder a esta pregunta: si ocurre el siguiente orden, ¿cuál es la probabilidad de que este orden sea mayor que un valor determinado? En otras palabras, ¿cuál es la probabilidad de ejecución de órdenes de diferentes profundidades (situación ideal, no tan rigurosa, en teoría el libro de órdenes tiene órdenes nuevas y cancelaciones, así como colas en la misma profundidad)?
El artículo está casi terminado y todavía quedan muchas preguntas por responder. La siguiente serie de artículos intentará dar respuestas.