En el artículo anterior se hizo una introducción preliminar a los métodos de cálculo de los distintos precios medios y se hizo una revisión del precio medio. En este artículo se continúa profundizando en este tema.

Datos requeridos

Los datos del flujo de órdenes y los diez niveles de datos de profundidad se recopilan a partir de operaciones reales, y la frecuencia de actualización es de 100 ms. El mercado real contiene únicamente los datos de compra y venta, que se actualizan en tiempo real. Por motivos de simplicidad, por el momento no se utiliza. Teniendo en cuenta que los datos son demasiado grandes, solo se conservan 100.000 filas de datos detallados y las condiciones del mercado para cada nivel también se separan en columnas separadas.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

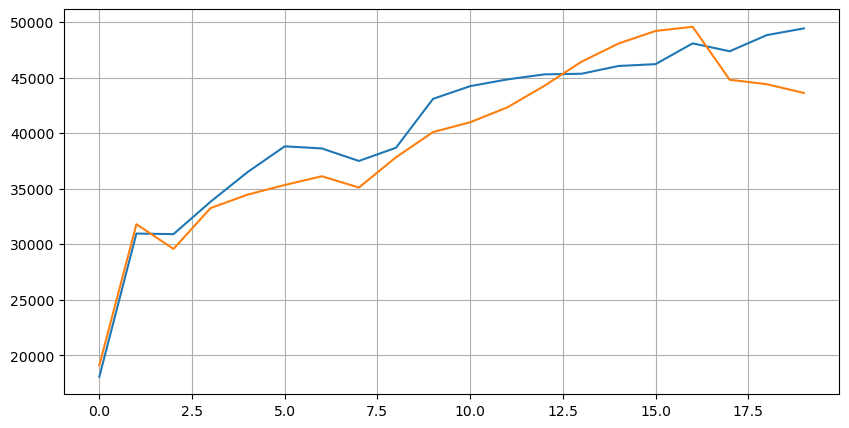
Veamos primero la distribución de estas 20 condiciones de mercado. Está en línea con las expectativas. Cuanto más lejos esté de la apertura del mercado, más órdenes pendientes habrá, y las órdenes de compra y las órdenes de venta son aproximadamente simétricas.

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

Combine datos de profundidad y datos de transacciones para facilitar la evaluación de la precisión del pronóstico. Aquí nos aseguramos de que los datos de la transacción sean posteriores a los datos de profundidad. Sin tener en cuenta el retraso, calculamos directamente el error cuadrático medio entre el valor previsto y el precio real de la transacción. Se utiliza para medir la precisión de las predicciones.

A juzgar por los resultados, el error de mid_price, el promedio del par de compra-venta, es el mayor. Después de cambiar a weight_mid_price, el error se vuelve inmediatamente mucho menor y se mejora aún más al ajustar el precio medio ponderado. Después de que se publicó el artículo de ayer, algunas personas informaron que solo habían usado I^³⁄₂. Lo revisé aquí y descubrí que el resultado era mejor. Después de pensar en la razón, debería ser la diferencia en la frecuencia de los eventos. Cuando I está cerca de -1 y 1, es un evento de baja probabilidad. Para corregir estas bajas probabilidades, la predicción de eventos de alta frecuencia No es tan preciso. Por lo tanto, para tener más en cuenta los eventos de alta frecuencia, ajusté los parámetros nuevamente (estos son parámetros puramente probados y el valor de referencia real no es muy significativo):

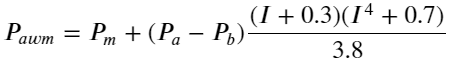
El resultado fue ligeramente mejor. Como se mencionó en el artículo anterior, las estrategias deben predecirse con más datos. Con más profundidad y datos de cumplimiento de pedidos, la mejora que se puede obtener mediante el enredo con el precio del mercado ya es muy débil.

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

Considere la profundidad del segundo engranaje

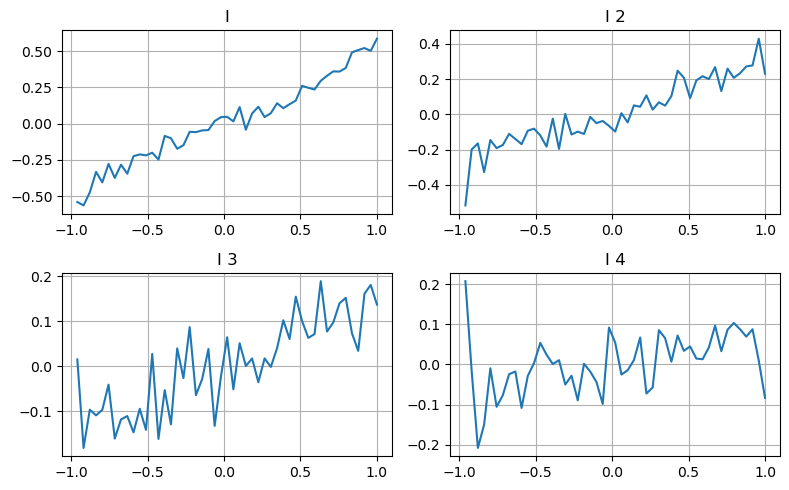
Aquí utilizamos la idea del artículo anterior de examinar los diferentes rangos de valores de un determinado parámetro de influencia y los cambios en el precio de transacción para medir la contribución de este parámetro al precio medio. Como se muestra en el gráfico de profundidad de primer nivel, a medida que I aumenta, es más probable que el precio de la próxima transacción cambie positivamente, lo que significa que I hace una contribución positiva.

El segundo lote se procesó de la misma manera y se encontró que, aunque el efecto era ligeramente menor que el del primer lote, todavía no era despreciable. El tercer nivel de profundidad también hace una ligera contribución, pero la monotonía es mucho peor y las profundidades mayores básicamente no tienen valor de referencia.

Según los diferentes niveles de contribución, se asignan diferentes pesos a los parámetros de desequilibrio de los tres niveles. La inspección real muestra que los errores de predicción se reducen aún más con los diferentes métodos de cálculo.

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

Considere los datos de transacciones

Los datos de las transacciones reflejan directamente el grado de posiciones largas y cortas. Después de todo, se trata de una opción que implica dinero real y el coste de realizar una orden es mucho menor, e incluso existen casos de fraude deliberado en la colocación de órdenes. Por lo tanto, a la hora de predecir el precio medio, la estrategia debe centrarse en los datos de las transacciones.

Considerando la forma, defina el desequilibrio en la cantidad promedio de llegada de órdenes VI, Vb, Vs representan la cantidad promedio de órdenes de compra y órdenes de venta dentro de un evento unitario respectivamente.

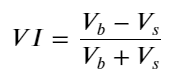
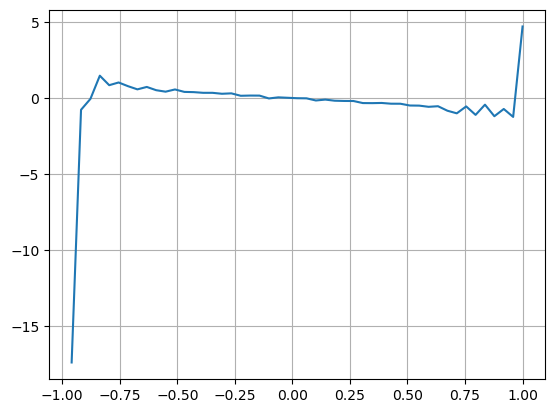
Los resultados muestran que la cantidad de llegada en un corto período de tiempo es la más significativa para predecir cambios de precios. Cuando el VI está entre (0,1-0,9), se correlaciona negativamente con el precio, pero fuera del rango se correlaciona positivamente con el precio. Esto sugiere que cuando el mercado no es extremo, se caracteriza principalmente por fluctuaciones y los precios volverán a la media. Cuando se dan condiciones extremas en el mercado, como una gran cantidad de órdenes de compra que superan a las órdenes de venta, la tendencia se saldrá de la tendencia. . Incluso si ignoramos estas situaciones de baja probabilidad y simplemente asumimos que la tendencia y el VI satisfacen una relación lineal negativa, el error de predicción del precio medio se reduce enormemente. La a en la fórmula representa el coeficiente.

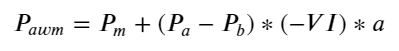
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

Precio medio integral

Teniendo en cuenta que tanto las órdenes pendientes como los datos de transacciones son útiles para predecir el precio medio, estos dos parámetros se pueden combinar. La asignación de peso aquí es arbitraria y no considera las condiciones límite. En casos extremos, el precio medio previsto puede ser No es entre comprar uno y vender uno, pero mientras se pueda reducir el error, estos detalles no importan.

Finalmente, el error de predicción se redujo de los 0,00487 iniciales a 0,0043. No entraremos en detalles aquí. Todavía hay mucho que explorar sobre el precio medio. Después de todo, predecir el precio medio es predecir el precio. Puedes probarlo tú mismo. .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

Resumir

Este documento combina datos de profundidad y datos de transacciones para mejorar aún más el método de cálculo del precio medio. Este documento proporciona un método para medir la precisión y mejora la precisión de las predicciones de cambios de precios. En general, los distintos parámetros no son muy rigurosos y son sólo de referencia. Con un precio medio más preciso, el siguiente paso es aplicarlo para realizar pruebas retrospectivas. Esta parte también tiene mucho contenido, por lo que dejaremos de actualizarla por un tiempo.